Sobel 导数

目录

• 目标
• 原理
  • Sobel 算子
  • 公式
• 代码
• 说明
  • 声明变量
  • 加载源图像
  • 减少噪声
  • 灰度化
  • Sobel 算子
  • 将输出转换为 CV_8U 图像
  • 梯度
  • 显示结果
• 结果

上一个教程： 为图像添加边框
下一个教程： 拉普拉斯算子

原作者	Ana Huamán
兼容性	OpenCV >= 3.0

目标

在本教程中，您将学习如何：

• 使用 OpenCV 函数 Sobel() 计算图像的导数。
• 使用 OpenCV 函数 Scharr() 计算大小为 \(3 \cdot 3\) 的核的更精确导数

原理

注意

以下说明摘自 Bradski 和 Kaehler 编著的学习 OpenCV一书。

1. 在过去两篇教程中，我们已经看到了卷积的应用性示例。最重要的卷积之一是计算图像中的导数（或导数的近似值）。
2. 为什么图像中的导数微积分如此重要？设想一下，想要检测图像中的边缘。例如

您会轻松注意到，在边缘处，像素强度会以显著的方式变化。表达变化的一种好方法是使用导数。梯度的剧烈变化表示图像中的重大变化。

1. 为了更直观，让我们假设我们有一幅一维图像。边缘在下面的图像中显示为强度“跳跃”

1. 如果对图像求一阶导数（实际上，这里显示为最大值），可以更轻松地看到边缘“跳跃”

1. 所以，从上述说明中，我们可以推断出一种在图像中检测边缘的方法，此方法可以通过找到梯度高于其相邻像素（或更一般化地说，高于阈值）的像素位置来执行。
2. 有关更详细的说明，请参考 Bradski 和 Kaehler 编著的学习 OpenCV

Sobel 算子

1. Sobel 算子是一种离散微分算子。它计算图像强度函数梯度的近似值。
2. Sobel 算子将高斯平滑和微分结合起来。

公式

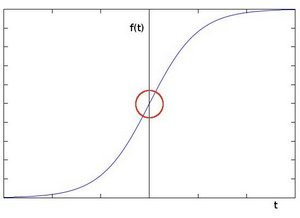
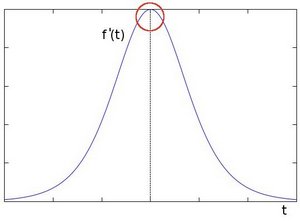
假设要操作的图像为 \(I\)

1. 计算两个导数
   1. 水平更改：这是通过用奇数大小的核 \(G_{x}\) 卷积 \(I\) 来计算的。例如，对于大小为 3 的核，\(G_{x}\) 的计算方式如下

\[G_{x} = \begin{bmatrix} -1 & 0 & +1 \\ -2 & 0 & +2 \\ -1 & 0 & +1 \end{bmatrix} * I\]

1. 垂直更改：这是通过用奇数大小的核 \(G_{y}\) 卷积 \(I\) 来计算的。例如，对于大小为 3 的核，\(G_{y}\) 的计算方式如下

\[G_{y} = \begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ +1 & +2 & +1 \end{bmatrix} * I\]

1. 在图像的每个点，我们通过组合上面两个结果，来计算该点处的梯度的一个近似值

   \[G = \sqrt{ G_{x}^{2} + G_{y}^{2} }\]

   虽然有时使用以下更简单的公式

   \[G = |G_{x}| + |G_{y}|\]

注意

当核的大小为 3 时，上面显示的 Sobel 核可能产生明显的误差（毕竟，Sobel 只是对导数的一种近似）。OpenCV 通过使用 Scharr() 函数解决大小为 3 的核的这种误差。此操作与标准的 Sobel 函数同样快，但更准确。它实现了以下核

\[G_{x} = \begin{bmatrix} -3 & 0 & +3 \\ -10 & 0 & +10 \\ -3 & 0 & +3 \end{bmatrix}\]

\[G_{y} = \begin{bmatrix} -3 & -10 & -3 \\ 0 & 0 & 0 \\ +3 & +10 & +3 \end{bmatrix}\]

你可以在 OpenCV 参考中查看有关此函数的更多信息 - Scharr() 。此外，在下面的示例代码中，你会注意到，在 Sobel() 函数的代码上方，还有一些 Scharr() 函数的注释代码。取消注释（显然要对 Sobel 代码进行注释）应该让你了解此函数如何工作。

代码

1. 这个程序的作用是什么？
   • 应用Sobel 算子，生成输出图像，其中检测到的边缘在较暗的背景上较亮。
2. 教程代码如下所示。

C++

你也可以从 这里 下载它

 
#include "opencv2/imgproc.hpp"
#include "opencv2/imgcodecs.hpp"
#include "opencv2/highgui.hpp"
 
#include <iostream>
 
using namespace cv;
using namespace std;
 
int main( int argc, char** argv )
{
  cv::CommandLineParser parser(argc, argv,
                               "{@input |lena.jpg|input image}"
                               "{ksize k|1|ksize (hit 'K' to increase its value at run time)}"
                               "{scale s|1|scale (hit 'S' to increase its value at run time)}"
                               "{delta d|0|delta (按 'D' 键在运行时增加其值)}"
                               "{help h|false|显示帮助消息}");
 
cout << "示例使用 Sobel 或 Scharr OpenCV 函数进行边缘检测\n\n";
parser.printMessage();
cout << "\n按 'ESC' 退出程序。\n按 'R' 重置值（ksize 将为 -1 等于 Scharr 函数）";
 
  // 首先声明我们将要使用的变量
  Mat image,src, src_gray;
  Mat grad;
  const String window_name = "Sobel 演示 - 简单边缘检测器";
  int ksize = parser.get<int>("ksize");
  int scale = parser.get<int>("scale");
  int delta = parser.get<int>("delta");
  int ddepth = CV_16S;
 
  String imageName = parser.get<String>("@input");
  // 像往常一样，我们加载源图像 (src)
image = imread( samples::findFile( imageName ), IMREAD_COLOR ); // 加载图像
 
  // 检查图像是否成功加载
  if( image.empty() )
  {
printf("打开图像时出错：%s\n", imageName.c_str());
    return EXIT_FAILURE;
  }
 
  for (;;)
  {
    // 通过高斯滤波（核大小 = 3）消除噪声
GaussianBlur(image, src, Size(3, 3), 0, 0, BORDER_DEFAULT);
 
    // 将图像转换为灰度
cvtColor(src, src_gray, COLOR_BGR2GRAY);
 
    Mat grad_x, grad_y;
    Mat abs_grad_x, abs_grad_y;
 
Sobel(src_gray, grad_x, ddepth, 1, 0, ksize, scale, delta, BORDER_DEFAULT);
 
Sobel(src_gray, grad_y, ddepth, 0, 1, ksize, scale, delta, BORDER_DEFAULT);
 
    // 转换回 CV_8U
convertScaleAbs(grad_x, abs_grad_x);
convertScaleAbs(grad_y, abs_grad_y);
 
addWeighted(abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad);
 
imshow(window_name, grad);
    char key = (char)waitKey(0);
 
    if(key == 27)
    {
      return EXIT_SUCCESS;
    }
 
    if (key == 'k' || key == 'K')
    {
ksize = ksize < 30 ? ksize+2 : -1;
    }
 
    如果 (键 == 's' 或键 == 'S')
    {
缩小++;
    }
 
    如果 (键 == 'd' 或键 == 'D')
    {
增量++;
    }
 
    如果 (键 == 'r' 或键 == 'R')
    {
      缩小 =  1;
ksize = -1;
增量 = 0;
    }
  }
  return EXIT_SUCCESS;
}

Java

您也可以从 此处 下载

 
导入 org.opencv.core.*;
导入 org.opencv.highgui.HighGui;
导入 org.opencv.imgcodecs.Imgcodecs;
导入 org.opencv.imgproc.Imgproc;
 
类 SobelDemoRun {
 
    public void 运行(String[] args) {
 
        // 首先声明我们将要使用的变量
Mat src, src_gray = new Mat();
Mat grad = new Mat();
String window_name = "Sobel Demo - Simple Edge Detector";
        int 缩小 = 1;
        int 增量 = 0;
        int ddepth = CvType.CV_16S;
 
        // 像往常一样，我们加载源图像 (src)
        // 检查参数数量
        如果 (args.length == 0){
System.out.println("参数不足！");
System.out.println("程序参数：[图像路径]");
System.exit(-1);
        }
 
        // 加载图像
src = Imgcodecs.imread(args[0]);
 
        // 检查图像是否成功加载
        如果( src.empty() ) {
System.out.println("打开图像错误："  + args[0]);
System.exit(-1);
        }
 
        // 通过高斯滤波（核大小 = 3）消除噪声
Imgproc.GaussianBlur( src, src, new Size(3, 3), 0, 0, Core.BORDER_DEFAULT );
 
        // 将图像转换为灰度
Imgproc.cvtColor( src, src_gray, Imgproc.COLOR_RGB2GRAY );
 
Mat grad_x = new Mat(), grad_y = new Mat();
Mat abs_grad_x = new Mat(), abs_grad_y = new Mat();
 
        //Imgproc.Scharr( src_gray, grad_x, ddepth, 1, 0, scale, delta, Core.BORDER_DEFAULT );
Imgproc.Sobel( src_gray, grad_x, ddepth, 1, 0, 3, scale, delta, Core.BORDER_DEFAULT );
 
        //Imgproc.Scharr( src_gray, grad_y, ddepth, 0, 1, scale, delta, Core.BORDER_DEFAULT );
Imgproc.Sobel( src_gray, grad_y, ddepth, 0, 1, 3, scale, delta, Core.BORDER_DEFAULT );
 
        // 转换回 CV_8U
Core.convertScaleAbs( grad_x, abs_grad_x );
Core.convertScaleAbs( grad_y, abs_grad_y );
 
Core.addWeighted( abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad );
 
HighGui.imshow( window_name, grad );
HighGui.waitKey(0);
 
System.exit(0);
    }
}
 
public class SobelDemo {
    public static void main(String[] args) {
        // 加载本机库。
System.loadLibrary(Core.NATIVE_LIBRARY_NAME);
        new SobelDemoRun().run(args);
    }
}

Python

您还可从 此处 下载

"""
@file sobel_demo.py
@brief 使用 Sobel 和/或 Scharr OpenCV 函数的示例代码，可创建一个简单的边缘检测器
"""
import sys
import cv2 as cv
 
 
def main(argv)
    
window_name = ('Sobel Demo - Simple Edge Detector')
scale = 1
delta = 0
ddepth = cv.CV_16S
    
 
    
    if len(argv) < 1
        print ('Not enough parameters')
        print ('Usage:\nmorph_lines_detection.py < path_to_image >')
        return -1
 
    # 加载图片
src = cv.imread(argv[0], cv.IMREAD_COLOR)
 
    # 检查图片是否加载正常
    if src is None
        print ('Error opening image: ' + argv[0])
        return -1
    
 
    
src = cv.GaussianBlur(src, (3, 3), 0)
    
 
    
gray = cv.cvtColor(src, cv.COLOR_BGR2GRAY)
    
 
    
grad_x = cv.Sobel(gray, ddepth, 1, 0, ksize=3, scale=scale, delta=delta, borderType=cv.BORDER_DEFAULT)
 
    # 梯度 Y
    # grad_y = cv.Scharr(gray,ddepth,0,1)
grad_y = cv.Sobel(gray, ddepth, 0, 1, ksize=3, scale=scale, delta=delta, borderType=cv.BORDER_DEFAULT)
    
 
    
abs_grad_x = cv.convertScaleAbs(grad_x)
abs_grad_y = cv.convertScaleAbs(grad_y)
    
 
    
grad = cv.addWeighted(abs_grad_x, 0.5, abs_grad_y, 0.5, 0)
    
 
    
    cv.imshow(window_name, grad)
    cv.waitKey(0)
    
 
    return 0
 
if __name__ == "__main__"
    main(sys.argv[1:])

说明

声明变量

  // 首先声明我们将要使用的变量
  Mat image,src, src_gray;
  Mat grad;
  const String window_name = "Sobel 演示 - 简单边缘检测器";
  int ksize = parser.get<int>("ksize");
  int scale = parser.get<int>("scale");
  int delta = parser.get<int>("delta");
  int ddepth = CV_16S;

加载源图像

  String imageName = parser.get<String>("@input");
  // 像往常一样，我们加载源图像 (src)
image = imread( samples::findFile( imageName ), IMREAD_COLOR ); // 加载图像
 
  // 检查图像是否成功加载
  if( image.empty() )
  {
printf("打开图像时出错：%s\n", imageName.c_str());
    return EXIT_FAILURE;
  }

减少噪点

    // 通过高斯滤波（核大小 = 3）消除噪声
GaussianBlur(image, src, Size(3, 3), 0, 0, BORDER_DEFAULT);

灰度

    // 将图像转换为灰度
cvtColor(src, src_gray, COLOR_BGR2GRAY);

Sobel 算子

 
    Mat grad_x, grad_y;
    Mat abs_grad_x, abs_grad_y;
 
Sobel(src_gray, grad_x, ddepth, 1, 0, ksize, scale, delta, BORDER_DEFAULT);
 
Sobel(src_gray, grad_y, ddepth, 0, 1, ksize, scale, delta, BORDER_DEFAULT);

• 我们在 x 和 y 方向计算“导数”。为此，我们使用 Sobel() 函数，如下所示：该函数采用以下参数

  • src_gray：在本例中为输入图像。在这里，它是 CV_8U
  • grad_x / grad_y ：输出图像。
  • ddepth：输出图像的深度。我们将它设置为 CV_16S 以避免溢出。
  • x_order：x 方向上导数的阶数。
  • y_order：y 方向上导数的阶数。
  • scale, delta 和 BORDER_DEFAULT：我们使用默认值。

  请注意，要计算 x 方向上的梯度，我们使用：\(x_{order}= 1\) 和\(y_{order} = 0\)。我们对 y 方向做类似的操作。

将输出转换为 CV_8U 图像

    // 转换回 CV_8U
convertScaleAbs(grad_x, abs_grad_x);
convertScaleAbs(grad_y, abs_grad_y);

梯度

 
addWeighted(abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad);

我们尝试通过添加两个方向梯度来近似计算梯度（请注意，这根本不是一个精确的计算，但对于我们的目的而言已经很好了）。

显示结果

imshow(window_name, grad);
    char key = (char)waitKey(0);

结果

1. 以下是给lena.jpg应用我们基本探测器的输出