改变图像的对比度和亮度！

目录

• 目标
• 理论
  • 图像处理
  • 像素转换
  • 亮度和对比度调整
• 代码
• 说明
• 结果
• 实际案例
  • 亮度和对比度调整
  • 伽玛校正
  • 校正曝光不足的图像
  • 代码
  • 附加资源

上一教程： 使用 OpenCV 添加（混合）两张图像
下一教程： 离散傅里叶变换

最初作者	Ana Huamán
兼容性	OpenCV >= 3.0

目标

在本教程中，您将学习如何

• 访问像素值
• 用零初始化矩阵
• 学习 cv::saturate_cast 的作用以及它的用途
• 了解一些关于像素转换的酷炫信息
• 在一个实际的例子中提高图像的亮度

理论

注意

下面的解释来自 Richard Szeliski 撰写的书 计算机视觉：算法与应用

图像处理

• 通用的图像处理操作符是一个函数，它接收一个或多个输入图像并生成一个输出图像。
• 图像转换可以看作
  • 点操作符（像素转换）
  • 邻域（基于区域的）操作符

像素转换

• 在这种类型的图像处理转换中，每个输出像素的值仅取决于对应的输入像素值（以及一些可能的全局收集信息或参数）。
• 此类操作符的示例包括亮度和对比度调整以及颜色校正和转换。

亮度和对比度调整

• 两个常用的点进程是乘法和加法，常量

  \[g(x) = \alpha f(x) + \beta\]

• 参数 \(\alpha > 0\) 和 \(\beta\) 通常称为增益和偏差参数；有时说这些参数分别控制对比度和亮度。

• 您可以将 \(f(x)\) 视为源图像像素，将 \(g(x)\) 视为输出图像像素。然后，我们可以更方便地将表达式写为

  \[g(i,j) = \alpha \cdot f(i,j) + \beta\]

  其中 \(i\) 和 \(j\) 表示像素位于第 i 行和第 j 列。

代码

C++

• 可下载代码: 点击 此处
• 以下代码执行操作：\(g(i,j) = \alpha \cdot f(i,j) + \beta\)

   
  #include "opencv2/imgcodecs.hpp"
  #include "opencv2/highgui.hpp"
  #include <iostream>
   
  // 我们此处没有“使用命名空间 std”，以避免 beta 变量和 c++17 中的 std::beta 之间发生冲突
  using std::cin;
  using std::cout;
  using std::endl;
  using namespace cv;
   
  int main( int argc, char** argv )
  {
      CommandLineParser parser( argc, argv, "{@input | lena.jpg | input image}" );
      Mat image = imread( samples::findFile( parser.get<String>( "@input" ) ) );
      if( image.empty() )
      {
  cout << "Could not open or find the image!\n" << endl;
  cout << "Usage: " << argv[0] << " <Input image>" << endl;
        return -1;
      }
   
      Mat new_image = Mat::zeros( image.size(), image.type() );
   
      double alpha = 1.0; /*< Simple contrast control */
      int beta = 0; /*< Simple brightness control */
   
  cout << " Basic Linear Transforms " << endl;
  cout << "-------------------------" << endl;
  cout << "* Enter the alpha value [1.0-3.0]: "; cin >> alpha;
  cout << "* Enter the beta value [0-100]: "; cin >> beta;
   
      for( int y = 0; y < image.rows; y++ ) {
          for( int x = 0; x < image.cols; x++ ) {
              for( int c = 0; c < image.channels(); c++ ) {
  new_image.在<Vec3b>(y,x)[c] =
  saturate_cast<uchar>( alpha*image.在<Vec3b>(y,x)[c] + beta );
              }
          }
      }
   
      imshow("原始图像", image);
      imshow("新图像", new_image);
   
      waitKey();
      return 0;
  }

Java

• 可下载代码：点击 此处
• 以下代码执行操作：\(g(i,j) = \alpha \cdot f(i,j) + \beta\)

  import java.util.Scanner;
   
  import org.opencv.core.Core;
  import org.opencv.core.Mat;
  import org.opencv.highgui.HighGui;
  import org.opencv.imgcodecs.Imgcodecs;
   
  class BasicLinearTransforms {
      private byte saturate(double val) {
          int iVal = (int) Math.round(val);
  iVal = iVal > 255 ? 255 : (iVal < 0 ? 0 : iVal);
          return (byte) iVal;
      }
   
      public void run(String[] args) {
  String imagePath = args.length > 0 ? args[0] : "../data/lena.jpg";
  Mat image = Imgcodecs.imread(imagePath);
          if (image.empty()) {
  System.out.println("Empty image: " + imagePath);
  System.exit(0);
          }
   
  Mat newImage = Mat.zeros(image.size(), image.type());
   
          double alpha = 1.0; /*< Simple contrast control */
          int beta = 0; /*< Simple brightness control */
   
  System.out.println(" Basic Linear Transforms ");
  System.out.println("-------------------------");
          try (Scanner scanner = new Scanner(System.in)) {
  System.out.print("* Enter the alpha value [1.0-3.0]: ");
  alpha = scanner.nextDouble();
  System.out.print("* Enter the beta value [0-100]: ");
  beta = scanner.nextInt();
          }
   
          byte[] imageData = new byte[(int) (image.total()*image.channels())];
  image.get(0, 0, imageData);
          byte[] newImageData = new byte[(int) (newImage.total()*newImage.channels())];
          for (int y = 0; y < image.rows(); y++) {
              for (int x = 0; x < image.cols(); x++) {
                  for (int c = 0; c < image.channels(); c++) {
                      double pixelValue = imageData[(y * image.cols() + x) * image.channels() + c];
  pixelValue = pixelValue < 0 ? pixelValue + 256 : pixelValue;
  newImageData[(y * image.cols() + x) * image.channels() + c]
  = saturate(alpha * pixelValue + beta);
                  }
              }
          }
  newImage.put(0, 0, newImageData);
   
  HighGui.imshow("Original Image", image);
  HighGui.imshow("New Image", newImage);
   
  HighGui.waitKey();
  System.exit(0);
      }
  }
   
  public class BasicLinearTransformsDemo {
      public static void main(String[] args) {
          // 加载本机 OpenCV 库
  System.loadLibrary(Core.NATIVE_LIBRARY_NAME);
   
          new BasicLinearTransforms().run(args);
      }
  }

Python

• 可下载代码：单击此处
• 以下代码执行操作：\(g(i,j) = \alpha \cdot f(i,j) + \beta\)

  from __future__ import print_function
  from builtins import input
  import cv2 as cv
  import numpy as np
  import argparse
   
  # 读取用户提供的图像
   
  parser = argparse.ArgumentParser(description='图像对比度和亮度变化代码！教程.')
  parser.add_argument('--input', help='输入图像的路径.', default='lena.jpg')
  args = parser.parse_args()
   
  image = cv.imread(cv.samples.findFile(args.input))
  如果 image 为 None
  打印（'无法打开或找到图像：'，args.input）
  退出（0）
   
   
   
  new_image = np.zeros(image.shape, image.dtype)
   
   
   
  alpha = 1.0 # 简单的对比度控制
  beta = 0 # 简单的亮度控制
   
  # 初始化值
  打印（' 基本线性变换 '）
  打印（'-------------------------'）
  尝试:
  alpha = float(输入（'* 输入 alpha 值 [1.0-3.0]：'）)
  beta = int(输入（'* 输入 beta 值 [0-100]：'）)
  捕获 ValueError
  打印（'错误，不是数字'）
   
   
  # 执行操作 new_image(i,j) = alpha*image(i,j) + beta
  # 我们可以使用以下方法来替换这些 'for' 循环
  # new_image = cv.convertScaleAbs(image, alpha=alpha, beta=beta)
  # 但我们想向你展示如何访问像素 :)
   
  对于 y 在 范围（image.shape[0]）
      对于 x 在 范围（image.shape[1]）
          对于 c 在 范围（image.shape[2]）
  new_image[y,x,c] = np.clip(alpha * image[y,x,c] + beta, 0, 255)
   
   
   
  cv.imshow('原始图像'，image)
  cv.imshow('新图像'，new_image)
   
  # 等待用户按某个键
  cv.waitKey()
   

说明

• 我们使用 cv::imread 加载图像，并将其保存为 Mat 对象

C++

    CommandLineParser parser( argc, argv, "{@input | lena.jpg | input image}" );
    Mat image = imread( samples::findFile( parser.get<String>( "@input" ) ) );
    if( image.empty() )
    {
cout << "Could not open or find the image!\n" << endl;
cout << "Usage: " << argv[0] << " <Input image>" << endl;
      return -1;
    }

Java

String imagePath = args.length > 0 ? args[0] : "../data/lena.jpg";
Mat image = Imgcodecs.imread(imagePath);
        if (image.empty()) {
System.out.println("Empty image: " + imagePath);
System.exit(0);
        }

Python

parser = argparse.ArgumentParser(description='图像对比度和亮度变化代码！教程.')
parser.add_argument('--input', help='输入图像的路径.', default='lena.jpg')
args = parser.parse_args()
 
image = cv.imread(cv.samples.findFile(args.input))
如果 image 为 None
打印（'无法打开或找到图像：'，args.input）
退出（0）

• 现在，由于我们将对该图像进行一些转换，我们需要一个新的 Mat 对象来存储它。此外，我们希望它具有以下特性
  • 初始像素值等于零
  • 与原始图像相同的大小和类型

C++

    Mat new_image = Mat::zeros( image.size(), image.type() );

Java

Mat newImage = Mat.zeros(image.size(), image.type());

Python

new_image = np.zeros(image.shape, image.dtype)

我们观察到 cv::Mat::zeros 返回基于 image.size() 和 image.type() 的 Matlab 风格的零初始化程序

• 我们现在要求用户输入 \(\alpha\) 和 \(\beta\) 的值

C++

    double alpha = 1.0; /*< Simple contrast control */
    int beta = 0; /*< Simple brightness control */
 
cout << " Basic Linear Transforms " << endl;
cout << "-------------------------" << endl;
cout << "* Enter the alpha value [1.0-3.0]: "; cin >> alpha;
cout << "* Enter the beta value [0-100]: "; cin >> beta;

Java

        double alpha = 1.0; /*< Simple contrast control */
        int beta = 0; /*< Simple brightness control */
 
System.out.println(" Basic Linear Transforms ");
System.out.println("-------------------------");
        try (Scanner scanner = new Scanner(System.in)) {
System.out.print("* Enter the alpha value [1.0-3.0]: ");
alpha = scanner.nextDouble();
System.out.print("* Enter the beta value [0-100]: ");
beta = scanner.nextInt();
        }

Python

alpha = 1.0 # 简单的对比度控制
beta = 0 # 简单的亮度控制
 
# 初始化值
打印（' 基本线性变换 '）
打印（'-------------------------'）
尝试:
alpha = float(输入（'* 输入 alpha 值 [1.0-3.0]：'）)
beta = int(输入（'* 输入 beta 值 [0-100]：'）)
捕获 ValueError
打印（'错误，不是数字'）

• 现在，要执行操作 \(g(i,j) = \alpha \cdot f(i,j) + \beta\)，我们将访问图像中的每个像素。由于我们使用 BGR 图像进行操作，每个像素将有三个值（B、G 和 R），因此我们也将分别访问它们。以下为该代码段

C++

    for( int y = 0; y < image.rows; y++ ) {
        for( int x = 0; x < image.cols; x++ ) {
            for( int c = 0; c < image.channels(); c++ ) {
new_image.在<Vec3b>(y,x)[c] =
saturate_cast<uchar>( alpha*image.在<Vec3b>(y,x)[c] + beta );
            }
        }
    }

Java

        byte[] imageData = new byte[(int) (image.total()*image.channels())];
image.get(0, 0, imageData);
        byte[] newImageData = new byte[(int) (newImage.total()*newImage.channels())];
        for (int y = 0; y < image.rows(); y++) {
            for (int x = 0; x < image.cols(); x++) {
                for (int c = 0; c < image.channels(); c++) {
                    double pixelValue = imageData[(y * image.cols() + x) * image.channels() + c];
pixelValue = pixelValue < 0 ? pixelValue + 256 : pixelValue;
newImageData[(y * image.cols() + x) * image.channels() + c]
= saturate(alpha * pixelValue + beta);
                }
            }
        }
newImage.put(0, 0, newImageData);

Python

对于 y 在 范围（image.shape[0]）
    对于 x 在 范围（image.shape[1]）
        对于 c 在 范围（image.shape[2]）
new_image[y,x,c] = np.clip(alpha * image[y,x,c] + beta, 0, 255)

请注意以下内容（仅限 C++ 代码）

• 为了访问图像中的每个像素，我们使用如下语法：image.at<Vec3b>(y,x)[c]，其中y是行，x是列，c是 B、G 或 R（0、1 或 2）。
• 由于运算\(\alpha \cdot p(i,j) + \beta\)可能会给出超出范围或非整数的值（如果\(\alpha\)是浮点数），我们使用cv::saturate_cast确保这些值有效。
• 最后，我们创建窗口并按照惯常方法显示图像。

C++

 
imshow("Original Image", image);
imshow("New Image", new_image);
 
waitKey();

Java

 
HighGui.imshow("Original Image", image);
HighGui.imshow("New Image", newImage);
 
HighGui.waitKey();

Python

# 显示内容
cv.imshow('原始图像'，image)
cv.imshow('新图像'，new_image)
 
# 等待用户按某个键
cv.waitKey()

注意

我们可以直接使用以下命令，而无需使用for循环来访问每个像素

C++

image.convertTo(new_image, -1, alpha, beta);

Java

image.convertTo(newImage, -1, alpha, beta);

Python

new_image = cv.convertScaleAbs(image, alpha=alpha, beta=beta)

其中cv::Mat::convertTo会有效地执行*new_image = a*image + beta*。但是，我们想向你展示如何访问每个像素。无论如何，这两种方法都会给出相同的结果，但是convertTo更加优化，并且运行速度快得多。

结果

• 运行我们的代码并使用\(\alpha = 2.2\)和\(\beta = 50\)

  $ ./BasicLinearTransforms lena.jpg
  基本线性变换
  -------------------------
  * 输入 alpha 值 [1.0-3.0]: 2.2
  * 输入 beta 值 [0-100]: 50

• 我们获得以下内容

实际示例

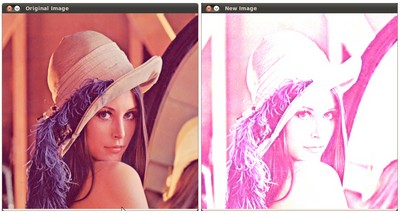
在本段中，我们将实践已学内容，通过调节图像的亮度和对比度，来校正曝光不足的图像。我们还将了解另一种校正图像亮度的技术，即伽马校正。

亮度和对比度调整

增加（/ 减少）\(\beta\)值会向每个像素添加（/ 减去）一个常量值。位于 [0 ; 255] 范围之外的像素值将饱和（即像素值高于 (/ 低于) 255 (/ 0) 将被夹制为 255 (/ 0)）。

浅灰色为原始图像的直方图，深灰色为 Gimp 中亮度 = 80 时

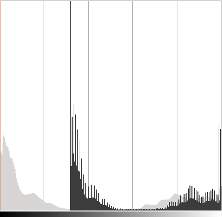
直方图对于每个颜色级别表示具有该级别颜色的像素数量。暗图像具有很多带有低颜色值的像素，因此其直方图会在其左部分呈现一个峰。叠加一个常量偏差后，由于我们为所有像素叠加了一个常量偏差，因此直方图向右移动。

\(\alpha\) 参数将修改级别展开方式。如果 \( \alpha < 1 \)，则颜色级别将被压缩，结果将是一幅对比度较小的图像。

浅灰色中，原始图像的直方图；深灰色中，Gimp 中对比度 < 0 时

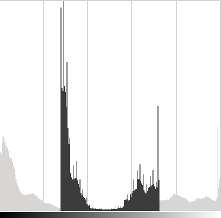
请注意，这些直方图已使用 Gimp 软件中的亮度-对比度工具获取。亮度工具应与 \(\beta\) 偏差参数相同，但对比度工具似乎不同于 \(\alpha\) 增益，且输出范围在 Gimp 中似乎是居中的（您可以在前一个直方图中注意到这一点）。

可能会发生这种情况，即使用 \(\beta\) 偏差可以提升亮度，但同时还会使图像略显朦胧，因为对比度会降低。可以使用 \(\alpha\) 增益来减弱这种效果，但由于饱和度，我们在原始亮部区域中会丢失一些细节。

Gamma 校正

Gamma 校正可用于通过在输入值和映射输出值之间使用非线性变换来校正图像亮度

\[O = \left( \frac{I}{255} \right)^{\gamma} \times 255\]

由于这一关系是非线性的，因此效果对于所有像素来说并不相同，而且将取决于它们的原始值。

针对不同 Gamma 值绘制曲线图

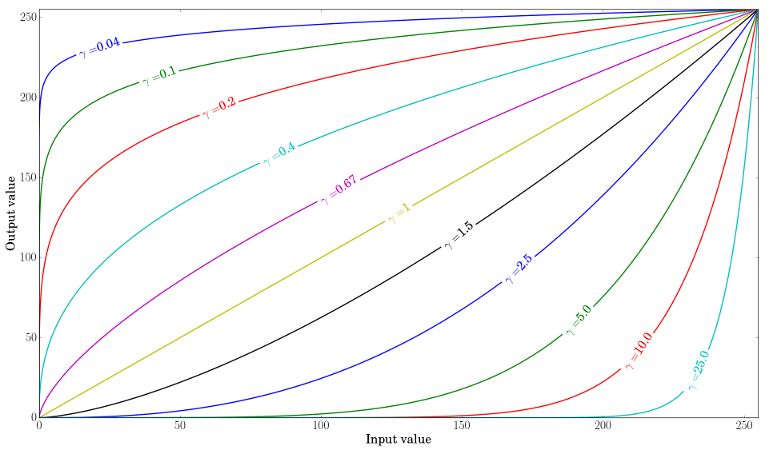
当 \( \gamma < 1 \) 时，原始暗区域将变得更亮，并且直方图向右移动，而当 \( \gamma > 1 \) 时则相反。

校正曝光不足的图像

已使用以下方式校正了以下图像：\( \alpha = 1.3 \) and \( \beta = 40 \)。

通过 Visem（自己的作品）[CC BY-SA 3.0]，来自 Wikimedia Commons

整体亮度已得到提升，但您会注意到由于使用的实现的数值饱和（摄影中的高光裁切），现在云层极度饱和。

已使用以下方式校正了以下图像: \( \gamma = 0.4 \)。

通过 Visem（自己的作品）[CC BY-SA 3.0]，来自 Wikimedia Commons

由于映射是非线性的，并且不存在如前一种方法中的数值饱和，因此 Gamma 校正趋于增加更少饱和度效果。

左：Alpha、贝塔校正后的直方图；中：原始图像的直方图；右：Gamma 校正后的直方图

上图 (y 轴范围对于三个直方图不同) 对比了这三张图像的直方图。你可以注意到对于原图来说，大多数像素值位于直方图的较低部分。在进行 \( \alpha \), \( \beta \) 校正之后，我们可以看到由于饱和而在 255 处有一个较大的峰值以及向右偏移。在进行伽马校正之后，直方图向右偏移，但黑暗区域的像素偏移更多 (参见 伽马曲线图)，比明亮区域的像素偏移更多。

在本教程中，你看到了两种简单的调节图像对比度和亮度的办法。它们是基本技术，不打算用作光栅图形编辑器的替代品！

代码

C++

本教程的代码在这里。

Java

本教程的代码在这里。

Python

本教程的代码在这里。

伽马校正代码

C++

    Mat lookUpTable(1, 256, CV_8U);
    uchar* p = lookUpTable.ptr();
    for( int i = 0; i < 256; ++i)
p[i] = saturate_cast<uchar>(pow(i / 255.0, gamma_) * 255.0);
 
    Mat res = img.clone();
LUT(img, lookUpTable, res);

Java

Mat lookUpTable = new Mat(1, 256, CvType.CV_8U);
        byte[] lookUpTableData = new byte[(int) (lookUpTable.total()*lookUpTable.channels())];
        for (int i = 0; i < lookUpTable.cols(); i++) {
lookUpTableData[i] = saturate(Math.pow(i / 255.0, gammaValue) * 255.0);
        }
lookUpTable.put(0, 0, lookUpTableData);
Mat img = new Mat();
Core.LUT(matImgSrc, lookUpTable, img);

Python

lookUpTable = np.empty((1,256), np.uint8)
    for i in range(256)
lookUpTable[0,i] = np.clip(pow(i / 255.0, gamma) * 255.0, 0, 255)
 
res = cv.LUT(img_original, lookUpTable)

查找表用于提高计算的性能，因为只需要计算一次 256 个值。

更多资源

• 图形渲染中的伽马校正

• 伽马校正和显示在 CRT 监视器上的图像

• 数字曝光技术