图像金字塔

目录

• 目标
• 理论
  • 图像金字塔
  • 高斯金字塔
• 代码
• 说明
  • 载入图像
  • 创建窗口
  • 循环
• 结果

上一教程： 使用形态学运算提取水平和垂直线
下一教程： 基本的阈值运算

原作者	Ana Huamán
兼容性	OpenCV >= 3.0

目标

本教程你将学习如何

• 使用 OpenCV 函数 pyrUp() 和 pyrDown() 对给定图像进行下采样或上采样。

理论

注释

以下解释来自 Bradski 和 Kaehler 撰写的书籍 学习 OpenCV。

• 我们通常需要将图像转换为不同于其原始尺寸的大小。为此，有两个可选项
  1. 放大图像（放大）或
  2. 缩小图像（缩小）。
• 尽管 OpenCV 中存在 - 字面意思上 - 调整图像大小的几何转换函数（resize，我们将在未来的教程中展示），但在本节中，我们将首先分析 图像金字塔 的使用，图像金字塔被广泛应用于大量的视觉应用程序中。

图像金字塔

• 图像金字塔是一个图像集合——全部源自单一原始图像——这些图像连续进行下采样，直至达到所需的某一终止点。
• 共有两种常见的图像金字塔
  • 高斯金字塔：用于对图像进行下采样
  • 拉普拉斯金字塔：用于从金字塔中分辨率较低（图像）的图像重建上采样图像
• 在本教程中，我们将使用高斯金字塔。

高斯金字塔

• 将金字塔想象成一组层，其中层越高，尺寸越小。

• 从底部到顶部对每一层进行编号，因此第\((i+1)\)层（表示为\(G_{i+1}\)）小于第\(i\)层（\(G_{i}\)）。

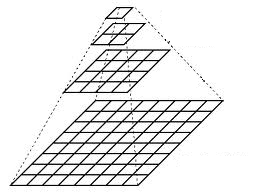
• 若要生成高斯金字塔中的第 \((i+1)\) 层，我们将执行以下操作

  • 用高斯核对 \(G_{i}\) 进行卷积

  \[\frac{1}{256} \begin{bmatrix} 1 & 4 & 6 & 4 & 1 \\ 4 & 16 & 24 & 16 & 4 \\ 6 & 24 & 36 & 24 & 6 \\ 4 & 16 & 24 & 16 & 4 \\ 1 & 4 & 6 & 4 & 1 \end{bmatrix}\]

  • 移除所有偶数行和偶数列。
• 你很容易会注意到，生成的图像面积正好是它前身图像面积的四分之一。对输入图像 \(G_{0}\)（原始图像）不断使用此过程可生成整个图像金字塔。
• 以上过程可用于对图像进行降采样。那么，如果我们要将其变大呢？
  • 首先，将图像尺寸放大到每个维度上原始图像的两倍，并使用新的偶数行和偶数列。
  • 使用上述相同的核（乘以 4）执行卷积，以估算“缺失像素”的值。
• 上述讲解的这两个过程（降采样和升采样）由 OpenCV 函数 pyrUp() 和 pyrDown() 实现，我们将在下面的代码示例中看到。

注释

当我们缩小图像的尺寸时，实际上是在丢失该图像的信息。

代码

本教程的代码如下所示。

C++

你还可以从 此处 下载。

 
#include "iostream"
#include "opencv2/imgproc.hpp"
#include "opencv2/imgcodecs.hpp"
#include "opencv2/highgui.hpp"
 
using namespace std;
using namespace cv;
 
const char* window_name = "Pyramids Demo";
 
int main( int argc, char** argv )
{
cout << "\n Zoom In-Out demo \n "
            "------------------ \n"
            " * [i] -> Zoom in \n"
            " * [o] -> Zoom out \n"
            " * [ESC] -> Close program \n" << endl;
 
    const char* filename = argc >=2 ? argv[1] : "chicky_512.png";
 
    // 加载图像
    Mat src = imread( samples::findFile( filename ) );
 
    // 检查图像是否已正常加载
    if(src.empty()){
printf(" Error opening image\n");
printf(" Program Arguments: [image_name -- default chicky_512.png] \n");
        return EXIT_FAILURE;
    }
 
    for(;;)
    {
imshow( window_name, src );
        char c = (char)waitKey(0);
 
        if( c == 27 )
{ break; }
        else if( c == 'i' )
pyrUp(src, src, Size(src.cols*2, src.rows*2 ));
printf( "** Zoom In: Image x 2 \n" );
        }
        else if( c == 'o' )
{ pyrDown(src, src, Size(src.cols/2, src.rows/2 ));
printf( "** Zoom Out: Image / 2 \n" );
        }
    }
 
    return EXIT_SUCCESS;
}

Java

您还可以在 此处 下载它

import org.opencv.core.*;
import org.opencv.highgui.HighGui;
import org.opencv.imgcodecs.Imgcodecs;
import org.opencv.imgproc.Imgproc;
 
class PyramidsRun {
 
String window_name = "Pyramids Demo";
 
    public void run(String[] args) {
System.out.println("\n" +
                " Zoom In-Out demo \n" +
                "------------------ \n" +
                " * [i] -> Zoom [i]n \n" +
                " * [o] -> Zoom [o]ut \n" +
                " * [ESC] -> Close program \n");
 
String filename = ((args.length > 0) ? args[0] : "../data/chicky_512.png");
 
        // 加载图像
Mat src = Imgcodecs.imread(filename);
 
        // 检查图像是否已正常加载
        if( src.empty() ) {
System.out.println("Error opening image!");
System.out.println("Program Arguments: [image_name -- default ../data/chicky_512.png] \n");
System.exit(-1);
        }
 
        while (true){
HighGui.imshow( window_name, src );
            char c = (char) HighGui.waitKey(0);
c = Character.toLowerCase(c);
 
            if( c == 27 ){
                break;
}else if( c == 'i'){
Imgproc.pyrUp(src, src, new Size(src.cols()*2, src.rows()*2));
System.out.println("** Zoom In: Image x 2");
}else if(c == 'o'){
Imgproc.pyrDown(src, src, new Size(src.cols()/2, src.rows()/2));
System.out.println("** Zoom Out: Image / 2");
            }
        }
 
System.exit(0);
    }
}
 
public class Pyramids {
    public static void main(String[] args) {
        // 加载本机库。
System.loadLibrary(Core.NATIVE_LIBRARY_NAME);
        new PyramidsRun().run(args);
    }
}

Python

您还可以从 此处 下载它

import sys
import cv2 as cv
 
 
def main(argv)
print("""
放大缩小演示
    ------------------
* [i] -> 放大 [i]
* [o] -> 缩小 [o]
* [ESC] -> 关闭程序
    """)
    
filename = argv[0] if len(argv) > 0 else 'chicky_512.png'
 
    # 加载图像
src = cv.imread(cv.samples.findFile(filename))
 
    # 检查图像是否加载正常
    if src is None
        print ('打开图像时出错！')
        print ('用法：pyramids.py [image_name -- default ../data/chicky_512.png] \n')
        return -1
    
    while 1:
rows, cols, _channels = map(int, src.shape)
        
        cv.imshow('金字塔演示', src)
        
k = cv.waitKey(0)
 
        if k == 27
            break
            
        elif chr(k) == 'i'
src = cv.pyrUp(src, dstsize=(2 * cols, 2 * rows))
            print ('** 放大: 图像 x 2')
            
        elif chr(k) == 'o'
src = cv.pyrDown(src, dstsize=(cols // 2, rows // 2))
            print ('** 缩小: 图像 / 2')
            
 
    cv.destroyAllWindows()
    return 0
 
if __name__ == "__main__"
    main(sys.argv[1:])

说明

让我们查看程序的一般结构

加载图像

C++

    const char* filename = argc >=2 ? argv[1] : "chicky_512.png";
 
    // 加载图像
    Mat src = imread( samples::findFile( filename ) );
 
    // 检查图像是否已正常加载
    if(src.empty()){
printf(" Error opening image\n");
printf(" Program Arguments: [image_name -- default chicky_512.png] \n");
        return EXIT_FAILURE;
    }

Java

String filename = ((args.length > 0) ? args[0] : "../data/chicky_512.png");
 
        // 加载图像
Mat src = Imgcodecs.imread(filename);
 
        // 检查图像是否已正常加载
        if( src.empty() ) {
System.out.println("Error opening image!");
System.out.println("Program Arguments: [image_name -- default ../data/chicky_512.png] \n");
System.exit(-1);
        }

Python

filename = argv[0] if len(argv) > 0 else 'chicky_512.png'
 
    # 加载图像
src = cv.imread(cv.samples.findFile(filename))
 
    # 检查图像是否加载正常
    if src is None
        print ('打开图像时出错！')
        print ('用法：pyramids.py [image_name -- default ../data/chicky_512.png] \n')
        return -1

创建窗口

C++

imshow( window_name, src );

Java

HighGui.imshow( window_name, src );

Python

        cv.imshow('金字塔演示', src)

循环

C++

    for(;;)
    {
imshow( window_name, src );
        char c = (char)waitKey(0);
 
        if( c == 27 )
{ break; }
        else if( c == 'i' )
pyrUp(src, src, Size(src.cols*2, src.rows*2 ));
printf( "** Zoom In: Image x 2 \n" );
        }
        else if( c == 'o' )
{ pyrDown(src, src, Size(src.cols/2, src.rows/2 ));
printf( "** Zoom Out: Image / 2 \n" );
        }
    }

Java

        while (true){
HighGui.imshow( window_name, src );
            char c = (char) HighGui.waitKey(0);
c = Character.toLowerCase(c);
 
            if( c == 27 ){
                break;
}else if( c == 'i'){
Imgproc.pyrUp(src, src, new Size(src.cols()*2, src.rows()*2));
System.out.println("** Zoom In: Image x 2");
}else if(c == 'o'){
Imgproc.pyrDown(src, src, new Size(src.cols()/2, src.rows()/2));
System.out.println("** Zoom Out: Image / 2");
            }
        }

Python

    while 1:
rows, cols, _channels = map(int, src.shape)
        
        cv.imshow('金字塔演示', src)
        
k = cv.waitKey(0)
 
        if k == 27
            break
            
        elif chr(k) == 'i'
src = cv.pyrUp(src, dstsize=(2 * cols, 2 * rows))
            print ('** 放大: 图像 x 2')
            
        elif chr(k) == 'o'
src = cv.pyrDown(src, dstsize=(cols // 2, rows // 2))
            print ('** 缩小: 图像 / 2')
            

执行等待用户输入的无限循环。如果用户按“ESC”，我们的程序将退出。此外，它有两个选项

• 执行上采样 - 放大“i”（在按“i”后）

  我们使用具有三个参数的函数 pyrUp()

  • src： 当前和目标图像（显示在屏幕上，可能是输入图像的两倍）
  • Size( tmp.cols*2, tmp.rows*2 )：目标大小。由于我们进行上采样，pyrUp() 预期尺寸是输入图像的两倍（在本例中为 src）。

C++

        else if( c == 'i' )
pyrUp(src, src, Size(src.cols*2, src.rows*2 ));
printf( "** Zoom In: Image x 2 \n" );
        }

Java

}else if( c == 'i'){
Imgproc.pyrUp(src, src, new Size(src.cols()*2, src.rows()*2));
System.out.println("** Zoom In: Image x 2");

Python

        elif chr(k) == 'i'
src = cv.pyrUp(src, dstsize=(2 * cols, 2 * rows))
            print ('** 放大: 图像 x 2')

• 执行下采样 - 放小“o”（在按“o”后）

  我们使用具有三个参数的函数 pyrDown()（类似于 pyrUp()）

  • src： 当前和目标图像（显示在屏幕上，可能是输入图像的一半）
  • Size( tmp.cols/2, tmp.rows/2 )：目标大小。由于我们进行下采样，pyrDown() 预期尺寸是输入图像的一半（在本例中为 src）。

C++

        else if( c == 'o' )
{ pyrDown(src, src, Size(src.cols/2, src.rows/2 ));
printf( "** Zoom Out: Image / 2 \n" );
        }

Java

}else if(c == 'o'){
Imgproc.pyrDown(src, src, new Size(src.cols()/2, src.rows()/2));
System.out.println("** Zoom Out: Image / 2");

Python

        elif chr(k) == 'o'
src = cv.pyrDown(src, dstsize=(cols // 2, rows // 2))
            print ('** 缩小: 图像 / 2')

请注意，重要的是输入图像可以除以二的倍数（在两个维度上）。否则，将会显示一个错误。

结果

• 该程序默认调用一个图像 chicky_512.png，该图像在 samples/data 文件夹中。请注意，此图像为 \(512 \times 512\)，因此下采样不会产生任何错误（ \(512 = 2^{9}\)）。原始图像如下所示

• 首先，我们通过按“d”应用两个连续的 pyrDown() 运算。我们的输出是

• 请注意，由于我们减小了图像尺寸，因此我们应该损失了一些分辨率。在我们应用 pyrUp() 两次（通过按“u”）后，这一点很明显。我们的输出现在是