目标

在本教程中，您将学习如何

使用 OpenCV 函数 cv::warpAffine 实现简单的重映射例程。
使用 OpenCV 函数 cv::getRotationMatrix2D 获取一个 \(2 \times 3\) 旋转矩阵

理论

什么是仿射变换？

一种可以表示为矩阵乘法（线性变换）后跟向量加法（平移）的变换。
从上面可以看出，我们可以使用仿射变换来表示
1. 旋转（线性变换）
2. 平移（向量加法）
3. 缩放操作（线性变换）
您可以看到，本质上，仿射变换表示两个图像之间的关系。
表示仿射变换的常用方法是使用 \(2 \times 3\) 矩阵。

\[ A = \begin{bmatrix} a_{00} & a_{01} \\ a_{10} & a_{11} \end{bmatrix}_{2 \times 2} B = \begin{bmatrix} b_{00} \\ b_{10} \end{bmatrix}_{2 \times 1} \]

\[ M = \begin{bmatrix} A & B \end{bmatrix} = \begin{bmatrix} a_{00} & a_{01} & b_{00} \\ a_{10} & a_{11} & b_{10} \end{bmatrix}_{2 \times 3} \]

考虑到我们想用 \(A\) 和 \(B\) 变换一个 2D 向量 \(X = \begin{bmatrix}x \\ y\end{bmatrix}\)，我们可以用

\(T = A \cdot \begin{bmatrix}x \\ y\end{bmatrix} + B\) 或 \(T = M \cdot [x, y, 1]^{T}\)

\[T = \begin{bmatrix} a_{00}x + a_{01}y + b_{00} \\ a_{10}x + a_{11}y + b_{10} \end{bmatrix}\]

如何获得仿射变换？

我们提到仿射变换基本上是两个图像之间的关系。关于这种关系的信息大致可以通过两种方式获得
1. 我们知道 \(X\) 和 T，也知道它们之间存在关系。那么我们的任务就是找到 \(M\)
2. 我们知道 \(M\) 和 \(X\)。为了得到 \(T\)，我们只需要应用 \(T = M \cdot X\)。我们关于 \(M\) 的信息可能是明确的（例如，具有 2×3 矩阵），或者可以作为点之间的几何关系来获得。
让我们用一种更好的方式解释这一点（b）。由于 \(M\) 关联 2 个图像，我们可以分析最简单的情况，即它关联两个图像中的三个点。看下图

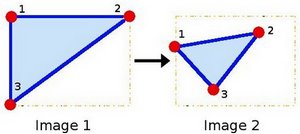
点 1、2 和 3（在图像 1 中形成一个三角形）映射到图像 2 中，仍然形成一个三角形，但现在它们已经发生了显著的变化。如果我们用这 3 个点（你可以根据自己的喜好选择它们）找到仿射变换，那么我们可以将这种找到的关系应用于图像中的所有像素。

代码

该程序做什么？
- 加载图像
- 对图像应用仿射变换。该变换是从三个点之间的关系中得到的。为此，我们使用函数 cv::warpAffine。
- 在变换后，对图像应用旋转。该旋转相对于图像中心。
- 等待用户退出程序

教程中的代码如下所示。您也可以从这里下载它

#include "opencv2/imgcodecs.hpp"

#include "opencv2/highgui.hpp"

#include "opencv2/imgproc.hpp"

#include <iostream>

using namespace cv;

using namespace std;

int main( int argc, char** argv )

{

CommandLineParser parser( argc, argv, "{@input | lena.jpg | input image}" );

Mat src = imread( samples::findFile( parser.get<String>( "@input" ) ) );

if( src.empty() )

{

cout << "无法打开或找到图像！\n" << endl;

cout << "用法: " << argv[0] << " <输入图像>" << endl;

return -1;

}

Point2f srcTri[3];

srcTri[0] = Point2f( 0.f, 0.f );

srcTri[1] = Point2f( src.cols - 1.f, 0.f );

srcTri[2] = Point2f( 0.f, src.rows - 1.f );

Point2f dstTri[3];

dstTri[0] = Point2f( 0.f, src.rows*0.33f );

dstTri[1] = Point2f( src.cols*0.85f, src.rows*0.25f );

dstTri[2] = Point2f( src.cols*0.15f, src.rows*0.7f );

Mat warp_mat = getAffineTransform( srcTri, dstTri );

Mat warp_dst = Mat::zeros( src.rows, src.cols, src.type() );

warpAffine( src, warp_dst, warp_mat, warp_dst.size() );

Point center = Point( warp_dst.cols/2, warp_dst.rows/2 );

double angle = -50.0;

double scale = 0.6;

Mat rot_mat = getRotationMatrix2D( center, angle, scale );

Mat warp_rotate_dst;

warpAffine( warp_dst, warp_rotate_dst, rot_mat, warp_dst.size() );

imshow( "源图像", src );

imshow( "Warp", warp_dst );

imshow( "Warp + Rotate", warp_rotate_dst );

waitKey();

return 0;

}

cv::CommandLineParser
专为命令行解析而设计。
定义 utility.hpp:820

cv::Mat
n 维密集数组类
定义 mat.hpp:812

cv::Mat::size
MatSize size
定义 mat.hpp:2160

cv::Mat::cols
int cols
定义 mat.hpp:2138

cv::Mat::empty
bool empty() const
如果数组没有元素，则返回 true。

cv::Mat::rows
int rows
行和列的数量，或者当矩阵具有超过 2 个维度时为 (-1, -1)
定义 mat.hpp:2138

cv::Mat::type
int type() const
返回矩阵元素的类型。

cv::Point_< float >

cv::String
std::string String
定义 cvstd.hpp:151

highgui.hpp

main
int main(int argc, char *argv[])
定义 highgui_qt.cpp:3

imgcodecs.hpp

imgproc.hpp

cv
与磁盘上的文件关联的文件存储的“黑盒”表示形式。
定义 core.hpp:102

std
STL 命名空间。

教程中的代码如下所示。您也可以从这里下载它
from __future__ import print_function

import cv2 as cv

import numpy as np

import argparse

parser = argparse.ArgumentParser(description='仿射变换教程代码.')

parser.add_argument('--input', help='输入图像路径。', default='lena.jpg')

args = parser.parse_args()

src = cv.imread(cv.samples.findFile(args.input))

if src is None

print('无法打开或找到图像：', args.input)

exit(0)

srcTri = np.array( [[0, 0], [src.shape[1] - 1, 0], [0, src.shape[0] - 1]] ).astype(np.float32)

dstTri = np.array( [[0, src.shape[1]*0.33], [src.shape[1]*0.85, src.shape[0]*0.25], [src.shape[1]*0.15, src.shape[0]*0.7]] ).astype(np.float32)

warp_mat = cv.getAffineTransform(srcTri, dstTri)

warp_dst = cv.warpAffine(src, warp_mat, (src.shape[1], src.shape[0]))

# 扭曲后旋转图像

center = (warp_dst.shape[1]//2, warp_dst.shape[0]//2)

angle = -50

scale = 0.6

rot_mat = cv.getRotationMatrix2D( center, angle, scale )

warp_rotate_dst = cv.warpAffine(warp_dst, rot_mat, (warp_dst.shape[1], warp_dst.shape[0]))

cv.imshow('源图像', src)

cv.imshow('扭曲', warp_dst)

cv.imshow('扭曲 + 旋转', warp_rotate_dst)

cv.waitKey()

cv::samples::findFile
cv::String findFile(const cv::String &relative_path, bool required=true, bool silentMode=false)
尝试查找请求的数据文件。

cv::imshow
void imshow(const String &winname, InputArray mat)
在指定窗口中显示图像。

cv::waitKey
int waitKey(int delay=0)
等待按键按下。

cv::imread
CV_EXPORTS_W Mat imread(const String &filename, int flags=IMREAD_COLOR)
从文件加载图像。

cv::warpAffine
void warpAffine(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar &borderValue=Scalar())
对图像应用仿射变换。

cv::getAffineTransform
Mat getAffineTransform(const Point2f src[], const Point2f dst[])
根据三对对应点计算仿射变换。

cv::getRotationMatrix2D
Mat getRotationMatrix2D(Point2f center, double angle, double scale)
计算二维旋转的仿射矩阵。
定义 imgproc.hpp:2582

说明

加载图像

C++

CommandLineParser parser( argc, argv, "{@input | lena.jpg | input image}" );

Mat src = imread( samples::findFile( parser.get<String>( "@input" ) ) );

if( src.empty() )

{

cout << "无法打开或找到图像！\n" << endl;

cout << "用法: " << argv[0] << " <输入图像>" << endl;

return -1;

}

Java

String filename = args.length > 0 ? args[0] : "../data/lena.jpg";

Mat src = Imgcodecs.imread(filename);

if (src.empty()) {

System.err.println("无法读取图像: " + filename);

System.exit(0);

}

Python

parser = argparse.ArgumentParser(description='仿射变换教程代码.')

parser.add_argument('--input', help='输入图像路径。', default='lena.jpg')

args = parser.parse_args()

src = cv.imread(cv.samples.findFile(args.input))

if src is None

print('无法打开或找到图像：', args.input)

exit(0)
仿射变换: 如上所述，我们需要两组 3 个点来推导出仿射变换关系。请看

C++

Point2f srcTri[3];

srcTri[0] = Point2f( 0.f, 0.f );

srcTri[1] = Point2f( src.cols - 1.f, 0.f );

srcTri[2] = Point2f( 0.f, src.rows - 1.f );

Point2f dstTri[3];

dstTri[0] = Point2f( 0.f, src.rows*0.33f );

dstTri[1] = Point2f( src.cols*0.85f, src.rows*0.25f );

dstTri[2] = Point2f( src.cols*0.15f, src.rows*0.7f );

Java

Point[] srcTri = new Point[3];

srcTri[0] = new Point( 0, 0 );

srcTri[1] = new Point( src.cols() - 1, 0 );

srcTri[2] = new Point( 0, src.rows() - 1 );

Point[] dstTri = new Point[3];

dstTri[0] = new Point( 0, src.rows()*0.33 );

dstTri[1] = new Point( src.cols()*0.85, src.rows()*0.25 );

dstTri[2] = new Point( src.cols()*0.15, src.rows()*0.7 );

Python

srcTri = np.array( [[0, 0], [src.shape[1] - 1, 0], [0, src.shape[0] - 1]] ).astype(np.float32)

dstTri = np.array( [[0, src.shape[1]*0.33], [src.shape[1]*0.85, src.shape[0]*0.25], [src.shape[1]*0.15, src.shape[0]*0.7]] ).astype(np.float32)

你可能想绘制这些点以更好地了解它们如何变化。它们的位置与示例图（在理论部分）中描绘的点的位置大致相同。你可以注意到由 3 个点定义的三角形的尺寸和方向发生了变化。
有了这两组点，我们可以使用 OpenCV 函数 cv::getAffineTransform 计算仿射变换

C++

Mat warp_mat = getAffineTransform( srcTri, dstTri );

Java

Mat warpMat = Imgproc.getAffineTransform( new MatOfPoint2f(srcTri), new MatOfPoint2f(dstTri) );

Python

warp_mat = cv.getAffineTransform(srcTri, dstTri)

我们得到一个 \(2 \times 3\) 矩阵作为输出（在本例中为 warp_mat）
然后我们将刚找到的仿射变换应用于 src 图像

C++

Mat warp_dst = Mat::zeros( src.rows, src.cols, src.type() );

warpAffine( src, warp_dst, warp_mat, warp_dst.size() );

Java

Mat warpDst = Mat.zeros( src.rows(), src.cols(), src.type() );

Imgproc.warpAffine( src, warpDst, warpMat, warpDst.size() );

Python

warp_dst = cv.warpAffine(src, warp_mat, (src.shape[1], src.shape[0]))

使用以下参数
- src: 输入图像
- warp_dst: 输出图像
- warp_mat: 仿射变换
- warp_dst.size(): 输出图像的期望尺寸
我们得到了第一张变换后的图像！我们将在下一步显示它。在这之前，我们还想旋转它...
旋转: 要旋转图像，我们需要知道两件事
1. 图像旋转的中心
2. 要旋转的角度。在 OpenCV 中，正角度表示逆时针方向
3. 可选: 缩放因子
我们使用以下代码片段定义这些参数

C++

Point center = Point( warp_dst.cols/2, warp_dst.rows/2 );

double angle = -50.0;

double scale = 0.6;

Java

Point center = new Point(warpDst.cols() / 2, warpDst.rows() / 2);

double angle = -50.0;

double scale = 0.6;

Python

center = (warp_dst.shape[1]//2, warp_dst.shape[0]//2)

angle = -50

scale = 0.6
我们使用 OpenCV 函数 cv::getRotationMatrix2D 生成旋转矩阵，该函数返回一个 \(2 \times 3\) 矩阵（在本例中为 rot_mat）

C++

Mat rot_mat = getRotationMatrix2D( center, angle, scale );

Java

Mat rotMat = Imgproc.getRotationMatrix2D( center, angle, scale );

Python

rot_mat = cv.getRotationMatrix2D( center, angle, scale )
现在我们将找到的旋转应用于之前变换的输出

C++

Mat warp_rotate_dst;

warpAffine( warp_dst, warp_rotate_dst, rot_mat, warp_dst.size() );

Java

Mat warpRotateDst = new Mat();

Imgproc.warpAffine( warpDst, warpRotateDst, rotMat, warpDst.size() );

Python

warp_rotate_dst = cv.warpAffine(warp_dst, rot_mat, (warp_dst.shape[1], warp_dst.shape[0]))
最后，我们在两个窗口中显示我们的结果，以及原始图像以供参考

C++

imshow( "源图像", src );

imshow( "Warp", warp_dst );

imshow( "Warp + Rotate", warp_rotate_dst );

Java

HighGui.imshow( "源图像", src );

HighGui.imshow( "Warp", warpDst );

HighGui.imshow( "Warp + Rotate", warpRotateDst );

Python

cv.imshow('源图像', src)

cv.imshow('扭曲', warp_dst)

cv.imshow('扭曲 + 旋转', warp_rotate_dst)
我们只需要等待用户退出程序

C++

waitKey();

Java

HighGui.waitKey(0);

Python

cv.waitKey()

结果

编译上面的代码后，我们可以将图像的路径作为参数传递给它。例如，对于像这样的图片

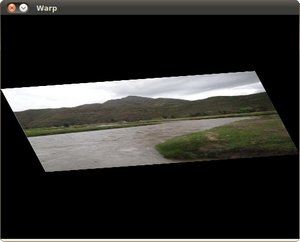
应用第一个仿射变换后，我们得到

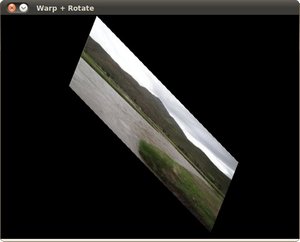
最后，应用负旋转（记住负表示顺时针方向）和缩放因子后，我们得到


原始作者	Ana Huamán
兼容性	OpenCV >= 3.0

目录

目标

理论

什么是仿射变换？

如何获得仿射变换？

代码

说明

结果