姿态计算概览

姿态计算问题 [182] 包括求解旋转和平移，使其最小化来自 3D-2D 点对应的重新投影误差。

solvePnP 和相关函数估算给定一组物体点、其对应的图像投影以及相机内参矩阵和畸变系数的对象姿态，请参阅下图（更确切地说，相机框架的 X 轴指向右侧，Y 轴向下，Z 轴向前）。

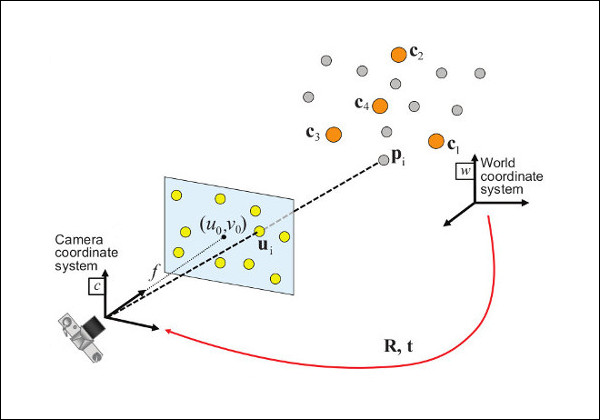
以世界坐标系 \( \bf{X}_w \) 表示的点使用透视投影模型 \( \Pi \) 和相机内参矩阵 \( \bf{A} \)（在文献中也表示为 \( \bf{K} \)）投影到图像平面上 \( \left[ u, v \right] \)。

\[ \begin{align*} \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} &= \bf{A} \hspace{0.1em} \Pi \hspace{0.2em} ^{c}\bf{T}_w \begin{bmatrix} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{bmatrix} \\ \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} &= \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{bmatrix} \end{align*} \]

因此，估计的姿态是旋转（rvec）和平移（tvec）向量，允许将以世界坐标系表示的 3D 点转换为相机坐标系

\[ \begin{align*} \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \end{bmatrix} &= \hspace{0.2em} ^{c}\bf{T}_w \begin{bmatrix} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{bmatrix} \\ \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \end{bmatrix} &= \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{bmatrix} \end{align*} \]

姿态计算方法

有关可能值列表，请参阅 cv::SolvePnPMethod 枚举文档。以下将介绍有关每种方法的一些详细信息

cv::SOLVEPNP_ITERATIVE 迭代方法基于 Levenberg-Marquardt 优化。在这种情况下，该函数会找到一个使重投影误差最小的位姿，即观测到的投影“imagePoints”和投影的（使用 cv::projectPoints ）“objectPoints”之间的平方距离之和。非平面“objectPoints”的初始解至少需要 6 个点，并使用 DLT 算法。平面“objectPoints”的初始解至少需要 4 个点，并使用透视分解的位姿。
cv::SOLVEPNP_P3P 该方法基于 X.S. Gao、X.-R. Hou、J. Tang、H.-F. Chang 撰写的论文“透视三点问题的完整解分类”（[98]）。在这种情况下，该函数明确需要四个目标点和图像点。
cv::SOLVEPNP_AP3P 该方法基于 T. Ke 和 S. Roumeliotis 撰写的论文“透视三点问题的有效代数解”（[145]）。在这种情况下，该函数明确需要四个目标点和图像点。
cv::SOLVEPNP_EPNP 该方法由 F. Moreno-Noguer、V. Lepetit 和 P. Fua 在“EPnP：有效透视 n 点相机位姿估计”论文中提出（[157]）。
cv::SOLVEPNP_DLS 实现损坏。使用该标志将回退到 EPnP。
该方法基于 J. Hesch 和 S. Roumeliotis 的论文：“PnP 的直接最小二乘 (DLS) 方法”（[125]）。
cv::SOLVEPNP_UPNP 实现损坏。使用该标志将回退到 EPnP。
该方法基于 A. Penate-Sanchez、J. Andrade-Cetto 和 F. Moreno-Noguer 的论文：“全面的线性化，用于鲁棒的相机位姿和焦距估计”（[213]）。在这种情况下，该函数还估计参数 \(f_x\) 和 \(f_y\)，并假定这两个参数值相同。然后，使用估计的焦距更新 cameraMatrix。
cv::SOLVEPNP_IPPE 该方法基于 T. Collins 和 A. Bartoli 的论文：“基于无穷小平面的位姿估计”（[61]）。该方法需要共面的目标点。
cv::SOLVEPNP_IPPE_SQUARE方法基于 Toby Collins 和 Adrien Bartoli 的论文。“基于无穷平面姿态估计”（[61])。此方法适用于标记姿态估计。它需要按以下顺序定义的 4 个共面目标点
- 点 0: [-squareLength / 2, squareLength / 2, 0]
- 点 1: [ squareLength / 2, squareLength / 2, 0]
- 点 2: [ squareLength / 2, -squareLength / 2, 0]
- 点 3: [-squareLength / 2, -squareLength / 2, 0]
cv::SOLVEPNP_SQPNP方法基于 G. Terzakis 和 M.Lourakis 的论文“一种一致快速且全局最优的视角 n 点问题解决方案”（[267]）。它需要 3 个或更多点。

P3P

cv::solveP3P()计算一个对象姿势，该姿势正好来自 3 个 3D-2D 点对应关系。P3P 问题最多有 4 个解决方案。

注意: 解决方案按投影误差（从最低到最高）排序。

PnP

cv::solvePnP()返回旋转和平移向量，将以对象坐标系表示的 3D 点转换到摄像机坐标系，使用不同的方法

P3P 方法（cv::SOLVEPNP_P3P，cv::SOLVEPNP_AP3P): 需要 4 个输入点才能返回一个惟一解决方案。
cv::SOLVEPNP_IPPE输入点必须 >= 4，并且目标点必须共面。
cv::SOLVEPNP_IPPE_SQUARE适用于标记姿态估计的特殊情况。输入点数量必须为 4。目标点必须按以下顺序定义
- 点 0: [-squareLength / 2, squareLength / 2, 0]
- 点 1: [ squareLength / 2, squareLength / 2, 0]
- 点 2: [ squareLength / 2, -squareLength / 2, 0]
- 点 3: [-squareLength / 2, -squareLength / 2, 0]
对于所有其他标志，输入点的数量必须 >= 4，目标点可以处于任何配置中。

通用 PnP

cv::solvePnPGeneric()允许检索所有可能的解决方案。

目前，仅 cv::SOLVEPNP_P3P、cv::SOLVEPNP_AP3P、cv::SOLVEPNP_IPPE、cv::SOLVEPNP_IPPE_SQUARE、cv::SOLVEPNP_SQPNP 可以返回多个解。

RANSAC PnP

cv::solvePnPRansac() 使用 RANSAC 方案计算对象姿态，该姿态与相机帧相关，目的是处理离群值。

可以在 [325] 中找到更多信息

姿势优化

姿态优化包含使用非线性最小化方法并从解决方案的初始估计开始估算最小化重投影误差的旋转和平移。OpenCV 为此问题提出了 cv::solvePnPRefineLM() 和 cv::solvePnPRefineVVS()。

cv::solvePnPRefineLM() 使用非线性 Levenberg-Marquardt 最小化方案 [178] [77]，当前实现将旋转更新计算为扰动，而不是在 SO(3) 中。

cv::solvePnPRefineVVS() 使用 Gauss-Newton 非线性最小化方案 [182]，并通过使用指数映射计算旋转部分的更新。

注意: 至少需要三个 3D-2D 点对应关系。