目标

在本教程中，您将学习简单阈值化、自适应阈值化和 Otsu 阈值化。
您将学习函数 cv.threshold 和 cv.adaptiveThreshold。

简单阈值化

此处的问题很简单。对每个像素应用相同的阈值。如果像素值小于阈值，则将其设置为 0，否则将其设置为最大值。函数 cv.threshold 用于应用阈值化。第一个参数是源图像，它应该是一个灰度图像。第二个参数是用于对像素值进行分类的阈值。第三个参数是分配给超过阈值的像素值的最大值。OpenCV 提供不同类型的阈值化，由函数的第四个参数给出。如上所述，基本阈值化通过使用类型 cv.THRESH_BINARY 来完成。所有简单阈值化类型为

有关差异，请参见这些类型的文档。

该方法返回两个输出。第一个是所使用的阈值，第二个输出是阈值化图像。

此代码比较了不同的简单阈值化类型

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
 
img = cv.imread('gradient.png', cv.IMREAD_GRAYSCALE)
assert img is not None, "file could not be read, check with os.path.exists()"
ret,thresh1 = cv.threshold(img,127,255,cv.THRESH_BINARY)
ret,thresh2 = cv.threshold(img,127,255,cv.THRESH_BINARY_INV)
ret,thresh3 = cv.threshold(img,127,255,cv.THRESH_TRUNC)
ret,thresh4 = cv.threshold(img,127,255,cv.THRESH_TOZERO)
ret,thresh5 = cv.threshold(img,127,255,cv.THRESH_TOZERO_INV)
 
标题 = ['原始图片','BINARY','BINARY_INV','TRUNC','TOZERO','TOZERO_INV']
图片 = [img, thresh1, thresh2, thresh3, thresh4, thresh5]
 
对于 i 在 6 的范围内
plt.子图(2,3,i+1),plt.imshow(images[i],'gray',最小值=0，最大值=255)
plt.标题(titles[i])
plt.x刻度([])，plt.y刻度([])
 
plt.展示()

注意: 为了绘制多张图片，我们使用了 plt.subplot() 函数。有关更多详细信息，请查看 matplotlib 文档。

该代码产生以下结果

图片

自适应阈值

在上一个部分，我们使用了一个阈值全局变量。但在所有情况下，这可能并不好，例如，如果一张图像的不同区域具有不同的光照条件。在这种情况下，自适应阈值可以提供帮助。在这里，算法根据像素周围一个小区域来确定像素的阈值。因此，对于同一图像的不同区域，我们获得了不同的阈值，其效果对光照变化的图像更好。

除了上面描述的参数外，此方法 cv.adaptiveThreshold 吸收三个输入参数

自适应方法决定如何计算阈值

cv.ADAPTIVE_THRESH_MEAN_C：阈值是邻域区域的平均值减去常量 C。
cv.ADAPTIVE_THRESH_GAUSSIAN_C：阈值是邻域值的高斯加权和减去常量 C。

块大小确定了邻域区域的大小，并且 C 是减去邻域像素的平均值或加权和的一个常量。

下面的代码比较了全局阈值算法和自适应阈值算法在光照变化的图像中应用的效果

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
 
img = cv.imread('sudoku.png', cv.IMREAD_GRAYSCALE)
assert img is not None, "file could not be read, check with os.path.exists()"
img = cv.medianBlur(img,5)
 
ret,th1 = cv.threshold(img,127,255,cv.THRESH_BINARY)
th2 = cv.adaptiveThreshold(img,255,cv.ADAPTIVE_THRESH_MEAN_C,\
cv.THRESH_BINARY,11,2)
th3 = cv.adaptiveThreshold(img,255,cv.ADAPTIVE_THRESH_GAUSSIAN_C,\
cv.THRESH_BINARY,11,2)
 
titles = ['原始图像', '全局阈值（v = 127)',
            '自适应均值阈值', '自适应高斯阈值']
images = [img, th1, th2, th3]
 
for i in range(4)
plt.subplot(2,2,i+1),plt.imshow(images[i],'gray')
plt.标题(titles[i])
plt.x刻度([])，plt.y刻度([])
plt.展示()

结果

图片

大津二值化

在全局阈值化中，我们使用任选值作为阈值。相比之下，大津方法无需选择值，而是自动确定值。

考虑仅具有两个不同图像值（双峰图像）的图像，其中直方图仅包含两个峰值。较好的阈值应位于这两个值之间。类似地，大津方法从图像直方图中确定最优的全局阈值。

为了实现此目的，使用了cv.threshold()函数，其中cv.THRESH_OTSU作为额外的标记传递。阈值可以选择任意值。然后该算法找到最优阈值，该阈值作为第一个输出值返回。

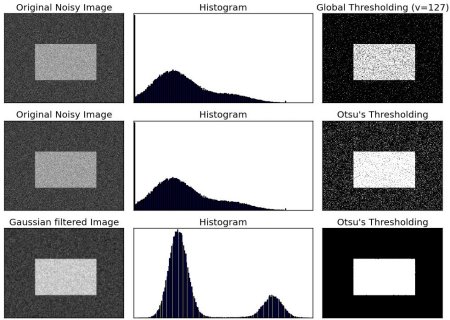
查看以下示例。输入图像为噪声图像。在第一种情况下，应用值为 127 的全局阈值化。在第二种情况下，直接应用大津阈值化。在第三种情况下，首先使用 5x5 高斯核滤波图像以去除噪声，然后应用大津阈值化。了解噪声滤波如何改善结果。

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
 
img = cv.imread('noisy2.png', cv.IMREAD_GRAYSCALE)
assert img is not None, "file could not be read, check with os.path.exists()"
 
# 全局阈值化
ret1,th1 = cv.threshold(img,127,255,cv.THRESH_BINARY)
 
# 大津阈值化
ret2,th2 = cv.threshold(img,0,255,cv.THRESH_BINARY+cv.THRESH_OTSU)
 
# 高斯滤波后的大津阈值化
blur = cv.GaussianBlur(img,(5,5),0)
ret3,th3 = cv.阈值(高斯模糊,0,255,cv.二进制阈值+cv.OTSU阈值)
 
# 绘制所有图片及其直方图
images = [img, 0, th1,
img, 0, th2,
高斯模糊, 0, th3]
titles = ['原始噪声图像','直方图','全局阈值（v=127）',
          '原始噪声图像','直方图','Otsu 阈值',
          '高斯滤波图像','直方图','Otsu 阈值']
 
对于 i 在 范围(3)
plt.subplot(3,3,i*3+1),plt.imshow(图像[i*3],'灰色')
plt.标题(标题[i*3]), plt.xticks([]), plt.yticks([])
plt.subplot(3,3,i*3+2),plt.hist(图像[i*3].ravel(),256)
plt.标题(标题[i*3+1]), plt.xticks([]), plt.yticks([])
plt.subplot(3,3,i*3+3),plt.imshow(图像[i*3+2],'灰色')
plt.标题(标题[i*3+2]), plt.xticks([]), plt.yticks([])
plt.展示()

结果

图片

Otsu 二值化是如何工作的？

本节演示了 Otsu 二值化的 Python 实现，以展示其实际工作原理。如果您不感兴趣，可以跳过此部分。

由于我们处理的是双峰图像，因此 Otsu 算法尝试找到一个阈值 (t)，它可以最小化由以下关系给出的加权类内方差

\[\sigma_w^2(t) = q_1(t)\sigma_1^2(t)+q_2(t)\sigma_2^2(t)\]

其中

\[q_1(t) = \sum_{i=1}^{t} P(i) \quad \& \quad q_2(t) = \sum_{i=t+1}^{I} P(i)\]

\[\mu_1(t) = \sum_{i=1}^{t} \frac{iP(i)}{q_1(t)} \quad \& \quad \mu_2(t) = \sum_{i=t+1}^{I} \frac{iP(i)}{q_2(t)}\]

\[\sigma_1^2(t) = \sum_{i=1}^{t} [i-\mu_1(t)]^2 \frac{P(i)}{q_1(t)} \quad \& \quad \sigma_2^2(t) = \sum_{i=t+1}^{I} [i-\mu_2(t)]^2 \frac{P(i)}{q_2(t)}\]

它实际上找到一个介于两个峰值之间的 t 值，使两类的方差最小。它可以用 Python 简单地实现，如下所示

img = cv.imread('noisy2.png', cv.IMREAD_GRAYSCALE)
assert img is not None, "file could not be read, check with os.path.exists()"
blur = cv.GaussianBlur(img,(5,5),0)
 
# 查找归一化的直方图及其累积分布函数
hist = cv.计算直方图([高斯模糊],[0],无,[256],[0,256])
hist_norm = hist.ravel()/hist.sum()
Q = hist_norm.cumsum()
 
bins = np.arange(256)
 
fn_min = np.inf
thresh = -1
 
对于 i 在 范围(1,256)
p1,p2 = np.hsplit(hist_norm,[i]) # 概率
q1,q2 = Q[i],Q[255]-Q[i] # 类的累加和
    如果 q1 < 1.e-6 或 q2 < 1.e-6
        继续
b1,b2 = np.hsplit(bins,[i]) # 权重
 
    # 查找均值和方差
m1,m2 = np.sum(p1*b1)/q1, np.sum(p2*b2)/q2
v1,v2 = np.sum(((b1-m1)**2)*p1)/q1,np.sum(((b2-m2)**2)*p2)/q2
 
    # 计算最小化函数
fn = v1*q1 + v2*q2
    如果 fn < fn_min
fn_min = fn
thresh = i
 
# 使用 OpenCV 函数查找 Otsu 阈值
ret, otsu = cv.threshold(blur,0,255,cv.THRESH_BINARY+cv.THRESH_OTSU)
print( "{} {}".format(thresh,ret) )

其他资源

Rafael C. Gonzalez 著，《数字图像处理》

练习

针对 Otsu 的二值化提供了一些优化。可以搜索并实现它。