光流

目标

• 我们将了解光流的概念及其使用卢卡斯-卡纳德法进行估算。
• 我们将使用 cv.calcOpticalFlowPyrLK() 等函数在视频中跟踪特征点。

光流

光流是在连续两帧之间图像对象由于物体或摄像机运动而产生的视运动模式。它是二维向量场，其中每个向量都是一个位移向量，显示了点从第一帧到第二帧的运动。请看下图（图片来源：维基百科光流文章）。

图片

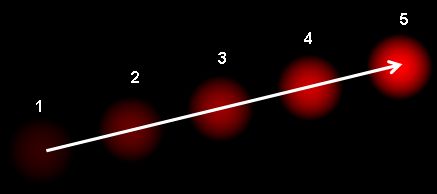
它显示了一个球在连续 5 帧中的运动。箭头显示了其位移向量。光流在以下领域有着广泛的应用：

• 运动结构
• 视频压缩
• 视频稳定 ...

光流基于以下几个假设：

1. 连续帧中对象的像素强度不发生变化。
2. 邻近像素具有相似的运动。

考虑第一帧中的一个像素\(I(x,y,t)\)（注意，这里加入了一个新的维度：时间。之前我们仅使用图像，因此不需要时间）。在经过\(dt\)时间拍摄的下一帧中，它移动了\((dx,dy)\)的距离。因此，由于这些像素是相同的且强度不变，我们可以说：

\[I(x,y,t) = I(x+dx, y+dy, t+dt)\]

然后取右侧泰勒级数近似，移除公共项并除以\(dt\)以得到以下方程：

\[f_x u + f_y v + f_t = 0 \;\]

其中：

\[f_x = \frac{\partial f}{\partial x} \; ; \; f_y = \frac{\partial f}{\partial y}\]

\[u = \frac{dx}{dt} \; ; \; v = \frac{dy}{dt}\]

上述方程称为光流方程。在其中，我们可以求出\(f_x\)和\(f_y\)，它们是图像梯度。同样，\(f_t\)是沿着时间方向的梯度。但 \((u,v)\) 是未知的。我们无法用一个包含两个未知变量的方程来求解。因此，有若干种方法可以求解此问题，其中一种就是卢卡斯-卡纳德法。

卢卡斯-卡纳德法

我们之前有一个预设，即所有邻近像素都将具有相似的动作。Lucas-Kanade 方法采用该点周围的 3x3 处的贴片。因此，所有 9 个点的动作都是相同的。我们可以为此 9 个点找到 \((f_x, f_y, f_t)\)。因此现在我们的问题变成了求解具有两个未知变量的 9 个方程，这是超定的。使用最小二乘拟合法可得到更好的解。下面是带有两个未知问题的两个方程，以及求解得到解的最终解。

\[\begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} \sum_{i}{f_{x_i}}^2 & \sum_{i}{f_{x_i} f_{y_i} } \\ \sum_{i}{f_{x_i} f_{y_i}} & \sum_{i}{f_{y_i}}^2 \end{bmatrix}^{-1} \begin{bmatrix} - \sum_{i}{f_{x_i} f_{t_i}} \\ - \sum_{i}{f_{y_i} f_{t_i}} \end{bmatrix}\]

(检查逆矩阵与 Harris 角点检测的相似性。它表示角点是我们跟踪的最佳点。)

因此，从用户的角度来看，想法很简单，我们提供一些点进行追踪，并接收这些点的光流矢量。但又存在一些问题。到目前为止，我们一直在处理小动作。因此，当出现大幅动作时，它就会失败。所以我们再次求助于金字塔。当我们进入金字塔时，会移除小动作，大幅动作也会变成小动作。因此在该处使用 Lucas-Kanade，我们就能在比例范围内获得光流。

OpenCV.js 中的 Lucas-Kanade 光流

我们使用以下函数：cv.calcOpticalFlowPyrLK (prevImg, nextImg, prevPts, nextPts, status, err, winSize = new cv.Size(21, 21), maxLevel = 3, criteria = new cv.TermCriteria(cv.TermCriteria_COUNT+ cv.TermCriteria_EPS, 30, 0.01), flags = 0, minEigThreshold = 1e-4)。

参数

prevImg	由 buildOpticalFlowPyramid 构建的第一个 8 位输入图像或金字塔。
nextImg	第二个输入图像或与 prevImg 大小和类型相同的金字塔。
prevPts	需要找到光流的 2D 点的矢量；点坐标必须是单精度浮点数。
nextPts	包含输入特征在第二个图像中计算出的新位置的 2D 点输出矢量（带有单精度浮点坐标）；当传递 cv.OPTFLOW_USE_ INITIAL_FLOW 标志时，矢量必须具有与输入中相同的大小。
status	输出状态矢量（无符号字符）；如果找到对应特征的光流，则矢量的每个元素设置为 1，否则设置为 0。
err	错误输出矢量；矢量的每个元素都将设置为对应特征的错误，错误度量类型可以在标志参数中进行设置；如果未找到该流，则不会定义错误（用状态参数查找此类情况）。
winSize	在每个金字塔级别搜索窗口的大小。
maxLevel	基于 0 的最大金字塔级别编号；如果设置为 0，则不使用金字塔（单级别），如果设置为 1，则使用两级，依此类推；如果将金字塔传递给输入，则算法将使用与金字塔一样多的级别，但不会超过 maxLevel。
criteria	指定迭代搜索算法终止条件的参数（在指定的最大迭代次数 criteria.maxCount 之后或搜索窗口移动幅度小于 criteria.epsilon 时）。
flags	操作标志 cv.OPTFLOW_USE_INITIAL_FLOW 使用初始估计值，存储在 nextPts 中；如果未设置此标志，则 prevPts 会复制到 nextPts，并被视为初始估计值。 cv.OPTFLOW_LK_GET_MIN_EIGENVALS 使用最小特征值作为错误度量（见 minEigThreshold 说明）；如果未设置此标志，则将窗口中像素数量除以初始点周围和移动点的块之间的 L1 距离用作错误度量。
minEigThreshold	算法计算光流方程 2x2 法向矩阵的最小特征值，除以窗口中像素的数量；如果此值小于 minEigThreshold，则将过滤相应的特征，且不处理其流，因此它允许移除错误点并提升性能。

使用说明

（此代码不会检查下一个关键点的正确性。所以即使图像中任何特征点消失，光流也有可能找到看起来很接近它的下一个点。所以实际上对于稳健的跟踪，应该在特定间隔内检测角点。）

OpenCV.js 中的光流密度

Lucas-Kanade 方法计算稀疏特征集的光流（在我们的示例中，使用 Shi-Tomasi 算法检测到的角点）。OpenCV.js 提供了另一种算法来找到光流密度。它计算帧中所有点的光流。它基于 Gunnar Farneback 的算法，该算法在 2003 年 Gunnar Farneback 的“基于多项式展开的两帧运动估算”中进行了说明。

我们使用如下函数：cv.calcOpticalFlowFarneback (prev, next, flow, pyrScale, levels, winsize, iterations, polyN, polySigma, flags)

参数

prev	第一个 8 位单通道输入图像。
下一个	第二个输入图像，大小和类型均与前一个相同。
流程	计算的流程图像，大小与前一个相同，类型为 CV_32FC2。
pyrScale	参数，指定图像大小 (<1) 以构建每个图像的金字塔；pyrScale=0.5 表示经典金字塔，其中每个后续层都比前一层小两倍。
levels	金字塔层数，包括初始图像；levels=1 表示不创建额外层，只使用原始图像。
winsize	平均窗口大小；值越大，算法对图像噪声的鲁棒性越高，并且快速运动检测的机会更大，但运动场会更加模糊。
iterations	算法在每个金字塔层执行的迭代次数。
polyN	用于在每个像素中查找多项式扩展的像素邻域的大小；值越大，意味着图像将被近似为更平滑的曲面，从而产生更健壮的算法和更模糊的运动场，通常 polyN =5 或 7。
polySigma	用作多项式扩展基础的高斯平滑导数的标准偏差；对于 polyN=5，可以设置 polySigma=1.1，对于 polyN=7，一个较好的值可能是 polySigma=1.5。
flags	操作标志，可以是以下组合 cv.OPTFLOW_USE_INITIAL_FLOW 将输入流程用作初始流程近似。 cv.OPTFLOW_FARNEBACK_GAUSSIAN 使用高斯 𝚠𝚒𝚗𝚜𝚒𝚣𝚎×𝚠𝚒𝚗𝚜𝚒𝚣𝚎 滤波器，而不是相同大小的盒子滤波器，进行光流估计；通常，此选项在速度较低的情况下提供的流程比盒子滤波器更准确；通常，应将高斯窗口的 winsize 设置为较大的值以实现相同级别的鲁棒性。

试用