 |
OpenCV 4.10.0
开源计算机视觉
|
 |
OpenCV 4.10.0
开源计算机视觉
|
在机器学习算法中,有一个训练数据概念。训练数据包含几个组成部分
如您所见,训练数据可能具有相当复杂的结构;此外,它可能非常大或并非全部可用,因此需要针对此概念进行抽象化。在 OpenCV ml 中,有一个 cv::ml::TrainData 类来解决此问题。
此简单分类模型设想,每个类的特征向量均服从正态分布(但不一定是独立分布)。因此,假定整个数据分布函数为高斯混合,每个类为一个组件。使用训练数据,该算法估算出每个类的均值向量和协方差矩阵,然后将其用于预测。
该算法缓存所有训练样本,并通过分析样本的特定数目 (K) 的最近邻 (使用投票、计算加权和等方法) 来预测新样本的响应。该方法有时称为“通过示例学习”,因为预测时,它查找与给定矢量最接近的具有已知响应的特征矢量。
最初,支持向量机 (SVM) 是一种构建最优二元 (2 类) 分类器的方法。后来,该方法扩展到回归和聚类问题。SVM 是基于核方法的部分案例。它使用核函数将特征矢量映射为更高维的空间,并在此空间或最优拟合训练数据的超平面中构建最优线性判别函数。对于 SVM,不会显式定义核。相反,需要定义超空间中任意 2 个点之间的距离。
解决方案是最佳的,这意味着(对于 2 类分类器)分离超平面和两个类最近特征矢量之间的间隔最大。最接近超平面的特征矢量称为支持矢量,这意味着其他矢量的位置不会影响超平面(决策函数)。
OpenCV 中的 SVM 实现基于 [50]
应该使用 StatModel::predict(samples, results, flags)。传递 flags=StatModel::RAW_OUTPUT 以从 SVM 中获取原始响应(对于回归、1 类或 2 类分类问题)。
本节讨论的 ML 类实现了在 [40] 中描述的分类和回归树算法。
类 cv::ml::DTrees 代表单个决策树或系列决策树。它也是 RTrees 和 Boost 的基类。
决策树是二叉树(每个非叶节点有两个子节点的树)。它可用于分类或回归。对于分类,每个树叶用类别标签标记;多个叶子可能具有相同的标签。对于回归,还向每个树叶分配常量,所以近似函数是分段常量。
要到达一个叶节点并获得输入特征向量的响应,预测程序从根节点开始。对于每个非叶节点,程序根据所观察节点中存储的特定索引变量的值,向左(选择左子节点作为下一个观察节点)或向右跳转。以下变量是可能的
因此,在每个节点中,都使用实体对(variable_index , decision_rule(阈值/子集))。此对称为拆分(对变量 variable_index 执行拆分)。一旦到达叶节点,就会将分配给此节点的值用作预测过程输出。
有时,输入向量的某些特征会丢失(例如,在黑暗中难以确定物体颜色),并且预测过程可能卡在特定节点中(在上述示例中,如果节点按颜色拆分)。为了避免这种情况,决策树使用所谓的代理拆分。也就是说,除了最佳“主”拆分之外,每个树节点还可以以几乎相同的结果拆分成一个或更多其他变量。
此树从根节点开始以递归方式进行构建。所有训练数据(特征向量和响应)用于拆分根节点。在每个节点中,最佳的决策规则(最优的“主”拆分)基于某些标准找到。在机器学习中,吉尼“纯度”标准用于分类,均方误差和用于回归。然后,如果需要,将找到替代拆分。这些拆分类似于在训练数据中主拆分的运行结果。所有数据使用主拆分和替代拆分(如同在预测程序中一样)在左子节点和右子节点之间进行划分。然后,此过程以递归方式拆分左右节点。在每个节点,递归过程在以下某个情况下可能会停止(即停止进一步拆分节点)
在构建树时,如有需要,可以利用交叉验证程序对树进行剪裁。也就是说,会剪掉可能导致模型过度拟合的树的一些枝。一般来说,仅将此过程应用于独立决策树。树集成通常会生成足够小的树,并采用其自己的保护方案来防止过度拟合。
除了预测(这是决策树的一个明显用途)外,此树还可用于各种数据分析。已构建决策树算法的一个关键属性是计算每个变量的重要程度(相对决策能力)的能力。例如,在使用消息中出现的一组词作为特征向量的垃圾邮件过滤器中,变量重要性评级可用于确定最能“指示垃圾邮件”的词,从而帮助将词典大小控制在合理范围。
每个变量的重要性是根据该变量在树中的所有拆分(包括主拆分和替代拆分)计算的。因此,要正确地计算变量的重要性,则即使没有缺失数据,也必须在训练参数中启用替代拆分。
一种常见的机器学习任务是有监督学习。在有监督学习中,目标是了解输入 \(x\) 和输出 \(y\) 之间的函数关系 \(F: y = F(x)\) 。预测定性输出称为分类,而预测定量输出称为回归。
Boosting 是一种强有力的学习概念,提供了解决监督分类学习任务的办法。它将许多“弱”分类器的性能组合起来,生成一个强大的委员会。[272] 弱分类器只需要比概率优胜,因此可以非常简单且低成本运算。然而,其中的许多分类器都巧妙地将结果组合为一个强大的分类器,该分类器通常优于大多数“单一”强大分类器,例如 SVM 和神经网络。
决策树是最常用的弱分类器,用在提升模式中。通常,每个树仅有一个单一分割节点的简单决策树(称为桩)就足够了。
提升模型基于 \(N\) 个训练示例 \({(x_i,y_i)}1N\),其中 \(x_i \in{R^K}\) 而 \(y_i \in{-1, +1}\)。\(x_i\) 是一个 \(K\) 分量向量。每个分量编码一个与学习任务相关的重要特征。所需的二分类输出编码为 -1 和 +1。
Boosting 的不同变体被称为离散 Adaboost、真实 AdaBoost、LogitBoost 和 Gentle AdaBoost [96]。它们在整体结构上非常相似。因此,本章仅重点介绍标准的二分类离散 AdaBoost 算法,如下概述。最初将相同的权重分配给每个样本(步骤 2)。然后,在加权训练数据(步骤 3a)上训练一个弱分类器 \(f_{m(x)}\)。计算它的加权训练误差以及比例因子 \(c_m\)(步骤 3b)。增加对被错误分类的训练样本的权重(步骤 3c)。然后对所有权重进行归一化,并继续寻找下一个弱分类器,持续执行另外 \(M\) -1 次。最终分类器 \(F(x)\) 是针对各个弱分类器的加权和的符号(步骤 4)。
二分类离散 AdaBoost 算法
为了在基本不损失准确性的情况下减少提升模型的计算时间,可以使用影响修剪技术。随着训练算法进行以及集成树数量增加,正确分类的训练样本数量不断增加并且置信度也不断增加,因此这些样例在后续迭代中接收到的权重也较小。相对权重很低的示例对弱分类器训练的影响很小。因此,在弱分类器训练期间,这种示例可以被排除,而不会对归纳分类器产生很大影响。此过程由 weight_trim_rate 参数控制。弱分类器训练仅使用权重总质量中摘要部分 weight_trim_rate 的示例。请注意,每次训练迭代时,都会重新计算所有训练样本的权重。一个特定迭代中删除的示例还可以用于学习一些更弱的分类器 [96]
应使用 StatModel::predict(samples, results, flags)。传递 flags=StatModel::RAW_OUTPUT 以获取 Boost 分类器的原始和。
随机树由 Leo Breiman 和 Adele Cutler 引入: http://www.stat.berkeley.edu/users/breiman/RandomForests/ 。该算法可以处理分类和回归问题。随机树是由树预测器收集起来的(集成),在本节中进一步称为森林(该术语也由 L. Breiman 引入)。分类的工作方式如下:随机树分类器接受输入特征向量,使用森林中的每棵树对其进行分类,然后输出接收“选票”最多的类标签。在回归的情况下,分类器响应是森林中所有树的响应的平均值。
所有的树都使用相同的参数进行训练,但是是在不同的训练集上进行训练。这些集合是使用自举法从原始训练集生成的:对于每个训练集,您可以从原始集合中随机选择相同数量的向量 (=N)。使用替换方式选择向量。也就是说,一些向量会多次出现,而另一些向量将不存在。在每棵训练出的树的每个节点,不是使用所有变量来找到最佳分割,而是使用随机子集。对每个节点都会生成一个新的子集。不过,它的对于所有的节点和所有的树来说都是固定的。默认情况下,它是一个训练参数,设置为\(\sqrt{变量数}\)。没有剪枝任何构建的树。
在随机树中,无需任何精度估计过程,如交叉验证或自举法,也不需单独的测试集来获取训练误差估值。误差在训练期间内部估值。如果当前树的训练集通过带放回的抽样绘制,则将遗漏一些向量(称为oob(bag 外)数据)。oob 数据的大小约为 N/3。分类误差估值使用 oob 数据,如下所示
关于随机树的使用示例,请参阅 OpenCV 分发中的 letter_recog.cpp 样本。
参考文献
期望最大化(EM)算法估算多元概率密度函数的参数,形式为具有指定混合数的高斯混合分布。
考虑从欧几里得 d 维空间抽取的高斯混合的 N 个特征向量的集合 { \(x_1, x_2,...,x_{N}\) }
\[p(x;a_k,S_k, \pi _k) = \sum _{k=1}^{m} \pi _kp_k(x), \quad \pi _k \geq 0, \quad \sum _{k=1}^{m} \pi _k=1,\]
\[p_k(x)= \varphi (x;a_k,S_k)= \frac{1}{(2\pi)^{d/2}\mid{S_k}\mid^{1/2}} exp \left \{ - \frac{1}{2} (x-a_k)^TS_k^{-1}(x-a_k) \right \} ,\]
其中,\(m\) 是混合数,\(p_k\) 是均值为 \(a_k\) 和协方差矩阵为 \(S_k\),\(\pi_k\) 是第 k 个混合的权重的正态分布密度。给定混合数 \(M\) 和样本 \(x_i\),\(i=1..N\),该算法查找所有混合参数的最大似然估计(MLE),即 \(a_k\),\(S_k\) 和 \(\pi_k\)
\[L(x, \theta )=logp(x, \theta )= \sum _{i=1}^{N}log \left ( \sum _{k=1}^{m} \pi _kp_k(x) \right ) \to \max _{ \theta \in \Theta },\]
\[\Theta = \left \{ (a_k,S_k, \pi _k): a_k \in \mathbbm{R} ^d,S_k=S_k^T>0,S_k \in \mathbbm{R} ^{d \times d}, \pi _k \geq 0, \sum _{k=1}^{m} \pi _k=1 \right \} .\]
EM 算法是一个迭代过程。每次迭代包括两步。第一步(期望步或 E 步)中,使用当前可用的混合参数估计来找到样本 i 属于混合 k 的概率 \(p_{i,k}\)(在下式中表示为 \(\alpha_{i,k}\))
\[\alpha _{ki} = \frac{\pi_k\varphi(x;a_k,S_k)}{\sum\limits_{j=1}^{m}\pi_j\varphi(x;a_j,S_j)} .\]
在第二步(极大化步或 M 步)中,使用计算出的概率来优化混合参数估计
\[\pi _k= \frac{1}{N} \sum _{i=1}^{N} \alpha _{ki}, \quad a_k= \frac{\sum\limits_{i=1}^{N}\alpha_{ki}x_i}{\sum\limits_{i=1}^{N}\alpha_{ki}} , \quad S_k= \frac{\sum\limits_{i=1}^{N}\alpha_{ki}(x_i-a_k)(x_i-a_k)^T}{\sum\limits_{i=1}^{N}\alpha_{ki}}\]
另外,当可以提供 \(p_{i,k}\) 的初始值时,算法可以从 M 步开始。当 \(p_{i,k}\) 未知时的另一个备选方案是使用一个更简单的聚类算法对输入样本进行预聚类,从而得到初始 \(p_{i,k}\) 。通常(包括机器学习),k 均值算法用于此目的。
EM 算法的一个主要问题是需要估计大量的参数。大部分参数位于协方差矩阵中,每个矩阵有 \(d \times d\) 个元素,其中 \(d\) 是特征空间维数。然而,在许多实际问题中,协方差矩阵接近于对角阵甚至接近于 \(\mu_k*I\),其中 \(I\) 是单位矩阵,\(\mu_k\) 是与混合有关的“尺度”参数。因此,一个稳健的计算方案可以从对协方差矩阵施加更严格的约束开始,然后使用估计出的参数作为受限更少的优化问题的输入(对角协方差矩阵通常已经是一个足够好的近似)。
参考文献
ML 实施前馈人工神经网络,或者更具体地说,多层感知器 (MLP),这是最常用的神经网络类型。MLP 包括输入层、输出层和一个或多个隐藏层。MLP 的每一层包括一个或多个神经元,这些神经元与前一层和后一层的多个神经元形成定向连接。以下示例表示一个 3 层感知器,它有三个输入、两个输出,并且隐藏层包括 5 个神经元
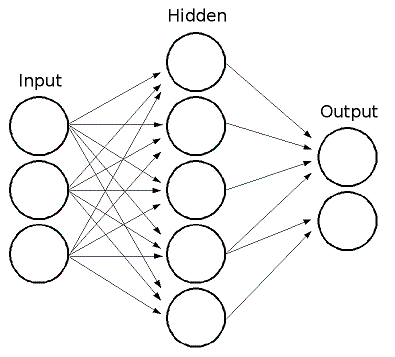
MLP 中的所有神经元都是相似的。每个神经元具有若干个输入连接(以来自上一层中的多个神经元的输出值作为输入)和多个输出连接(将结果传递给下一层中的多个神经元)。从上一层检索的值将与特定权重(针对每个神经元为个别值)加上偏置术语求和。会使用激活函数 \(f\)(对于不同的神经元可能也有所不同)转换该和值。
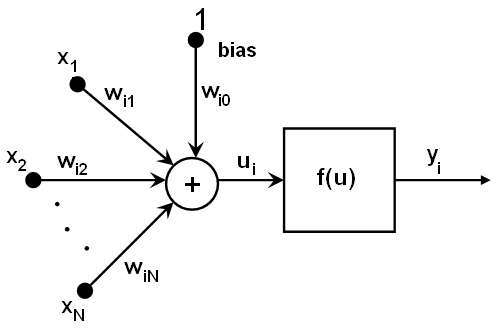
换句话说,给定层 \(n\) 的输出 \(x_j\),层 \n+1\) 的输出 \(y_i\) 将被计算为:
\[u_i = \sum _j (w^{n+1}_{i,j}*x_j) + w^{n+1}_{i,bias}\]
\[y_i = f(u_i)\]
可以使用不同的激活函数。ML 实现了三个标准函数
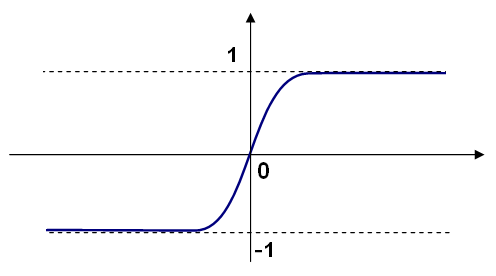
在 ML 中,所有神经元具有相同的激活函数,具有由用户指定的相同的自由参数(\(\alpha, \beta\),并且不会被训练算法改变。
因此,整个经过训练的网络的工作方式如下
因此,为计算该网络,需要了解所有权重 \(w^{n+1)}_{i,j}\)。权重由训练算法计算。该算法采用训练集(具有对应输出向量的多个输入向量),并迭代调整权重,以让网络对所提供的输入向量做出所需响应。
网络大小越大(隐藏层的数量及其大小),潜在的网络灵活性就越大。训练集上的误差可以任意减小。但同时,学习的网络也“学习”训练集中的噪声,因此当网络大小达到极限后,测试集上的误差通常会开始增加。此外,与较小的网络相比,较大的网络训练时间长得多,因此使用cv::PCA或类似技术对数据进行预处理,并针对关键特征训练较小的网络是合理的。
另一个 MLP 功能是无法按原样处理类别数据。但是,存在一种解决方法。如果输入或输出(对于 \ (n>2\) 的 n 级分类器)层中的某个特征是类别特征,并且可以取 \ (M>2\) 个不同的值,则将其表示为 M 个元素的二元元组是有意义的,其中第 i 个元素仅在特征等于 i -当 th 值超出 M 个可能值时为 1。它增加了输入/输出层的尺寸,但也加速了训练算法的收敛,同时启用了此类变量的“模糊”值,即概率元组而不是固定值。
ML 实现了两种训练 MLP 的算法。第一个算法是经典的随机顺序反向传播算法。第二个(默认)算法是批处理 RPROP 算法。
ML 实现了逻辑回归,这是一种概率分类技术。逻辑回归是一种二进制分类算法,与支持向量机(SVM)密切相关。与 SVM 一样,逻辑回归可以扩展到解决多类分类问题,如数字识别(即识别给定图像中的数字 0,1 2, 3,...)。此版本的逻辑回归支持二进制和多类分类(对于多类,它创建了多个 2 类分类器)。为了训练逻辑回归分类器,使用批处理梯度下降和迷你批处理梯度下降算法(参见 http://en.wikipedia.org/wiki/Gradient_descent_optimization)。逻辑回归是一种判别分类器(有关详细信息,请参阅 http://www.cs.cmu.edu/~tom/NewChapters.html)。逻辑回归在 LogisticRegression 中实现为 C++ 类。
在逻辑回归中,我们尝试优化训练参数 \(\theta\),以实现假设 \(0 \leq h_\theta(x) \leq 1\)。我们有 \(h_\theta(x) = g(h_\theta(x))\) 和 \(g(z) = \frac{1}{1+e^{-z}}\) 作为逻辑或 sigmoid 函数。逻辑回归中的“Logistic”一词指此函数。对于给定的 0 和 1 类的二进制分类问题数据,可以确定给定的数据实例属于类 1(如果 \(h_\theta(x) \geq 0.5\),或者类 0(如果 \(h_\theta(x) < 0.5\))。
在逻辑回归中,选择正确的参数对于减少训练误差和确保较高的训练精度至关重要
Logistic 回归分类器的训练参数样本集可以按如下方式进行初始化
 1.9.8 于 2024 年 6 月 2 日星期日 21:52:13 为 OpenCV 生成的
1.9.8 于 2024 年 6 月 2 日星期日 21:52:13 为 OpenCV 生成的