理解 K 均值聚类

目标

在本章中，我们将理解 K 均值聚类的概念，它的工作原理等等。

理论

我们将借助一个常用的示例来对此进行说明。

T 恤尺码问题

考虑一家公司，它将向市场发布一种新型 T 恤。显然，他们必须制造不同尺码的型号来满足各种体型的人。因此，该公司制作了一个包含人们身高和体重的数据库，并将其绘制到下方的图表中

图像

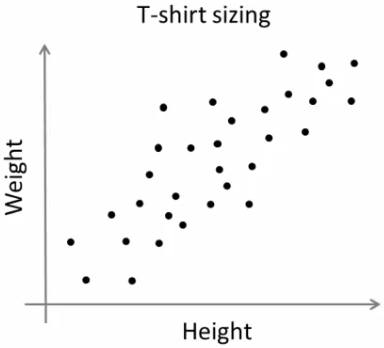
公司无法制造各种尺码的 T 恤。相反，他们将人群分为小号、中号和大号，仅制造 3 种模型，这些模型适用于所有人。将人分组到三组中可以通过 k 均值聚类来完成，并且该算法为我们提供了最适合所有人的 3 种尺码。如果不行的话，公司可以将人群分为更多组，可能是五组，依此类推。查看下方图像

图像

它如何工作？

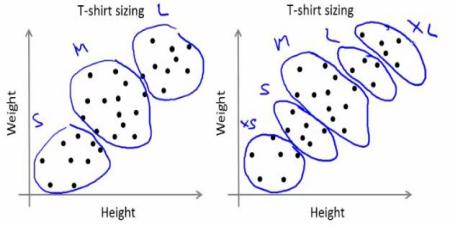
这种算法是一个迭代过程。我们将在图像的帮助下逐步对其进行解释。

考虑如下数据集（你可以将其视为 T 恤问题）。我们需要将此数据聚类到两个组中。

图像

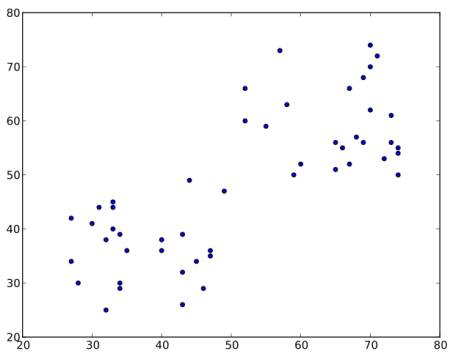
步骤 1 - 算法随机选择两个质心，\(C1\) 和 \(C2\)（有时，任何两个数据都被视为质心）。

步骤 2 - 它计算每个点到两个质心的距离。如果测试数据更接近于 \(C1\)，那么该数据将标记为“0”。如果它更接近于 \(C2\)，则标记为“1”（如果存在更多质心，则标记为“2”、“3”等）。

在我们的例子中，我们将所有标记为“0”的数据着色为红色，将标记为“1”的数据着色为蓝色。因此，我们在上述操作后得到以下图像。

图像

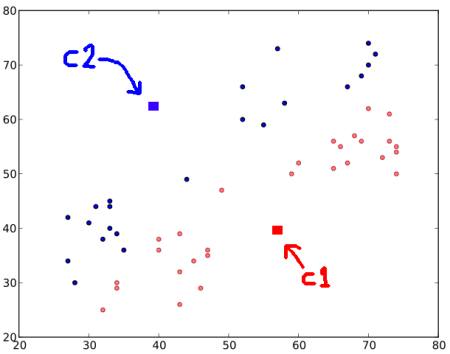
步骤 3 - 接下来我们分别计算所有蓝点和红点的平均值，这将成为我们的新质心。也就是说，\(C1\) 和 \(C2\) 转移到新计算出的质心（请记住，显示的图像不是真实值，也不是真实比例，仅用于演示）。

再次使用新的质心执行步骤 2，并将数据标记为“0”和“1”。

因此，我们得到如下结果

图像

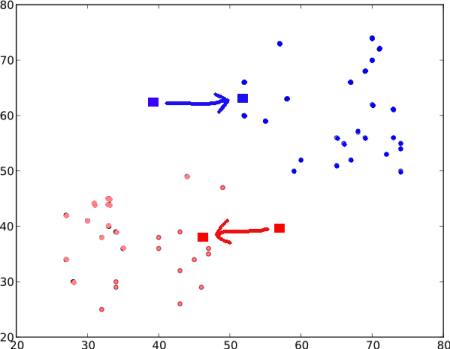
现在步骤 - 2和步骤 - 3会迭代进行，直到两个质心收敛到固定点。*（或者根据我们提供的条件，如最大迭代次数或达到特定精度等条件停止。）* **这些点使得测试数据与它们对应的质心之间的距离和最小。**或者，简单地说，\(C1 \leftrightarrow Red\_Points\)和\(C2 \leftrightarrow Blue\_Points\)之间的距离和最小。

\[最小化 \;\bigg[J = \sum_{所有\: Red\_Points}distance(C1,Red\_Point) + \sum_{所有\: Blue\_Points}distance(C2,Blue\_Point)\bigg]\]

最终结果大致如下所示

图像

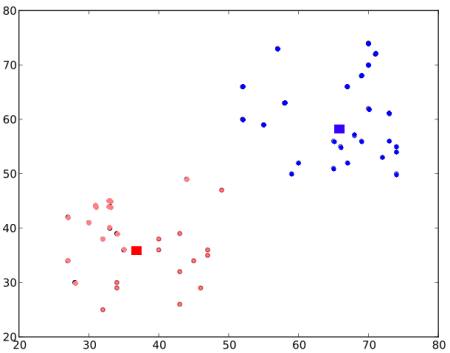
因此，这只是对 K 均值聚类的一种直观理解。有关详细信息和数学解释，请阅读任何标准机器学习教科书或查看其他资源中的链接。这只是 K 均值聚类的表层知识。此算法还有很多修改，如如何选择初始质心，如何加速迭代过程等等。

其他资源

1. 机器学习课程，吴恩达教授的视频讲座（有些图片取自该课程）

练习