快速鲁棒特征（SURF）简介

目标

本章，

• 我们将了解 SURF 的基础知识
• 我们将了解 OpenCV 中的 SURF 功能

理论

在上一章，我们了解到 SIFT 可用于关键点检测和描述。但它的速度相对较慢，人们需要更快的版本。2006 年，Bay、H.、Tuytelaars、T. 和 Van Gool、L 三人发表了一篇名为“SURF：快速鲁棒特征”的论文，介绍了一种名为 SURF 的新算法。顾名思义，它是 SIFT 的速度优化版。

在 SIFT 中， 对于尺度空间的查找，Lowe 通过高斯差分逼近高斯拉普拉斯算子。SURF 再进一步，通过盒状滤波器来逼近拉普拉斯算子。下图展示了此类逼近方式的演示。这种逼近方式的一个巨大优势在于，借助积分图像，可以使用盒状滤波器轻松计算卷积。而且可以对不同的尺度并行执行此操作。此外，SURF 依赖于尺度和位置的 Hessian 矩阵行列式。

图像

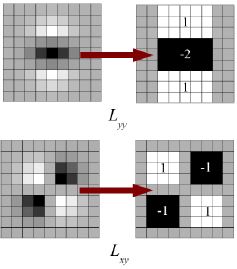
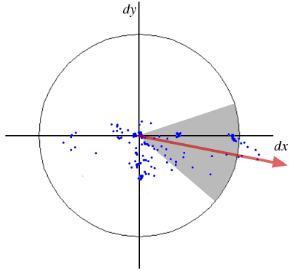
对于方向分配，SURF 在大小 6s 的邻域使用水平和垂直方向的小波响应。还对其应用了适当的高斯权重。然后将它们绘制在给定图像中的空间中。通过计算 60 度角的滑动方向窗口中的所有响应之和来估算主要方向。有趣的是，在任何尺度上都可以非常轻松地使用积分图像找出小波响应。对于许多应用程序来说，不需要旋转不变性，因此无需找出此方向，这加快了流程。SURF 提供了一种名为直立 SURF 或 U-SURF 的功能。它提高了速度，并且对 \(\pm 15^{\circ}\) 具有鲁棒性。OpenCV 支持这两种功能，具体取决于标志 upright。如果它为 0，则计算方向。如果它为 1，则不计算方向，而且速度更快。

图像

对于特征描述，SURF 使用水平和垂直方向的小波响应（同样，积分图像的使用简化了问题）。沿关键点周围取大小为 20sX20s 的邻域，其中 s 是大小。它被划分为 4x4 的子区域。对于每个子区域，取水平和垂直小波响应，并以如下方式形成一个向量，\(v=( \sum{d_x}, \sum{d_y}, \sum{|d_x|}, \sum{|d_y|})\)。当将此作为向量表示时，会得到一个总共 64 级的 SURF 特征描述符。维度越低，计算和匹配的速度就越高，但会提供更好的特征独特性。

为了获得更高的辨识度，SURF 特征描述符有一个扩展的 128 维版本。\(d_x\) 和 \(|d_x|\) 的总和分别针对 \(d_y < 0\) 和 \(d_y \geq 0\) 计算。类似地，\(d_y\) 和 \(|d_y|\) 的总和会按照 \(d_x\) 的符号进行拆分，从而使特征的数量翻倍。它不会增加太多计算复杂度。OpenCV 通过将标志extended 的值设置成 0 和 1 分别支持 64 维和 128 维（默认值是 128 维）

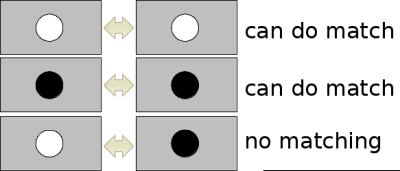
另一个重要的改进是使用拉普拉斯算子符号（Hessian 矩阵迹）作为底层兴趣点。由于在检测过程中已经计算过，所以这不会增加计算成本。拉普拉斯算子符号将暗背景上的亮斑与反向情况区分开来。在匹配阶段，我们仅在它们具有相同对比度类型的情况下比较特征（如下面的图像所示）。这种最小信息允许进行更快的匹配，而不会降低描述符的性能。

图像

简而言之，SURF 在每个步骤中都添加了许多特征以提高速度。分析表明，它比 SIFT 快 3 倍，而性能与 SIFT 相当。SURF 擅长处理模糊和旋转的图像，但不太擅长处理视点变化和光照变化。

OpenCV 中的 SURF

OpenCV 提供了类似 SIFT 的 SURF 功能。你可以通过一些可选条件（例如 64/128 维描述符、直立/正常 SURF 等）来启动一个 SURF 对象。所有详细信息都在文档中得到很好的解释。然后，就像我们在 SIFT 中所做的那样，我们可以使用 SURF.detect()、SURF.compute() 等来查找关键点和描述符。

首先，我们将看到一个简单的演示，说明如何查找 SURF 关键点和描述符并绘制它。所有示例都在 Python 终端中显示，因为它与 SIFT 相同。

>>> img = cv.imread('fly.png', cv.IMREAD_GRAYSCALE)
 
# 创建 SURF 对象。你可以在此处或稍后指定参数。
# 在此处我将 Hessian 阈值设置为 400
>>> surf = cv.xfeatures2d.SURF_create(400)
 
# 直接查找关键点和描述符
>>> kp, des = surf.detectAndCompute(img,None)
 
>>> len(kp)
 699

1199 个关键点太多，无法显示在图片中。我们将它减少到大约 50 个，以便在图像上绘制它。在匹配时，我们可能需要所有这些特征，但现在不需要。因此，我们增加了 Hessian 阈值。

# 检查当前 Hessian 阈值
>>> print( surf.getHessianThreshold() )
400.0
 
# 我们将其设置为大约 50000。记住，这只是为了在图片中显示。
# 在实际情况下，最好使用 300-500 的值
>>> surf.setHessianThreshold(50000)
 
# 再次计算关键点并检查其数量。
>>> kp, des = surf.detectAndCompute(img,None)
 
>>> print( len(kp) )
47

它小于 50。我们将其绘制在图像上。

>>> img2 = cv.drawKeypoints(img,kp,None,(255,0,0),4)
 
>>> plt.imshow(img2),plt.show()

查看下面的结果。您将看到 SURF 更类似于斑点探测器。它检测到蝴蝶翅膀上的白色斑点。您可以在其他图片上对其进行测试。

图像

现在我想应用 U-SURF，这样它就不会找到方向。

# 检查直立标志，如果为 False，则将其设为 True
>>> print( surf.getUpright() )
False
 
>>> surf.setUpright(True)
 
# 重新计算特征点并绘制它
>>> kp = surf.detect(img,None)
>>> img2 = cv.drawKeypoints(img,kp,None,(255,0,0),4)
 
>>> plt.imshow(img2),plt.show()

查看下面的结果。所有方向都显示在同一方向中。它比以前快。如果您从事方向不是问题（比如全景缝合）等的情形，这会更好。

图像

最后，我们检查描述符大小，如果它仅为 64 维，则将其更改为 128。

# 查找描述符大小
>>> print( surf.descriptorSize() )
64
 
# 那意味着标志“扩展”为 False。
>>> surf.getExtended()
 False
 
# 因此，我们将其设为 True 以获得 128 维描述符。
>>> surf.setExtended(True)
>>> kp, des = surf.detectAndCompute(img,None)
>>> print( surf.descriptorSize() )
128
>>> print( des.shape )
(47, 128)

剩余部分是在另一章中要讲的匹配。

其他资源

练习