目标

本章内容

我们将直观地理解SVM。

理论

线性可分数据

考虑下图，其中包含两种类型的数据，红色和蓝色。在kNN中，对于测试数据，我们过去常常测量它与所有训练样本的距离，并选择距离最小的样本。测量所有距离需要大量时间，存储所有训练样本需要大量内存。但是，考虑到图像中给出的数据，我们是否需要那么多呢？

图像

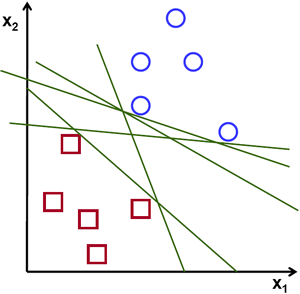
考虑另一种方法。我们找到一条线，\(f(x)=ax_1+bx_2+c\)，它将数据分成两个区域。当我们得到一个新的测试数据\(X\)时，只需将其代入\(f(x)\)。如果\(f(X) > 0\)，则属于蓝色组，否则属于红色组。我们可以将这条线称为决策边界。它非常简单且内存高效。这种可以用直线（或高维空间中的超平面）分成两部分的数据称为线性可分。

所以在上面的图像中，你可以看到有很多这样的线是可能的。我们应该选择哪一条？我们可以直观地说，这条线应该尽可能远离所有点。为什么？因为输入数据中可能存在噪声。这些数据不应该影响分类精度。因此，选择最远的一条线将提供更多抗噪能力。所以SVM所做的是找到一条直线（或超平面），使其到训练样本的最小距离最大。请参见下图中穿过中心的粗线。

图像

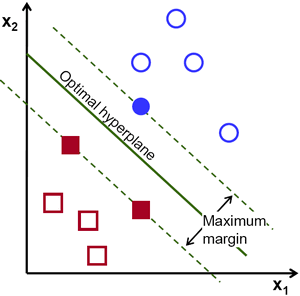
因此，要找到这个决策边界，需要训练数据。需要全部数据吗？不需要。只需要那些靠近相反组的数据就足够了。在我们的图像中，它们是一个蓝色填充的圆圈和两个红色填充的正方形。我们可以称它们为支持向量，通过它们的线称为支持平面。它们足以找到我们的决策边界。我们不必担心所有数据。它有助于减少数据量。

发生的情况是，首先找到两个最能代表数据的超平面。例如，蓝色数据由\(w^Tx+b_0 > 1\)表示，而红色数据由\(w^Tx+b_0 < -1\)表示，其中\(w\)是权重向量（\(w=[w_1, w_2,..., w_n]\)）而\(x\)是特征向量（\(x = [x_1,x_2,..., x_n]\)）。\(b_0\)是偏差。权重向量决定决策边界的方向，而偏差点决定其位置。现在决策边界定义为这两个超平面之间的中点，因此表示为\(w^Tx+b_0 = 0\)。支持向量到决策边界的最小距离由下式给出，\(distance_{support \, vectors}=\frac{1}{||w||}\)。边距是此距离的两倍，我们需要最大化此边距。即我们需要最小化一个新的函数\(L(w, b_0)\)，它有一些约束条件，可以表示如下

\[\min_{w, b_0} L(w, b_0) = \frac{1}{2}||w||^2 \; \text{受限于} \; t_i(w^Tx+b_0) \geq 1 \; \forall i\]

其中\(t_i\)是每个类的标签，\(t_i \in [-1,1]\).

非线性可分数据

考虑一些不能用直线分成两部分的数据。例如，考虑一个一维数据，其中'X'位于-3和+3，'O'位于-1和+1。显然它不是线性可分的。但是有一些方法可以解决这些问题。如果我们可以用函数\(f(x) = x^2\)映射这个数据集，我们会得到'X'为9，'O'为1，它们是线性可分的。

否则，我们可以将这个一维数据转换为二维数据。我们可以使用\(f(x)=(x,x^2)\)函数来映射此数据。然后'X'变为(-3,9)和(3,9)，而'O'变为(-1,1)和(1,1)。这也是线性可分的。简而言之，低维空间中非线性可分数据更有可能在高维空间中变为线性可分。

通常，可以将d维空间中的点映射到某个D维空间\((D>d)\)来检查线性可分的可能性。有一种方法可以帮助通过在低维输入（特征）空间中执行计算来计算高维（核）空间中的点积。我们可以用下面的例子来说明。

考虑二维空间中的两个点，\(p=(p_1,p_2)\)和\(q=(q_1,q_2)\)。令\(\phi\)为一个映射函数，它将二维点映射到三维空间，如下所示

\[\phi (p) = (p_{1}^2,p_{2}^2,\sqrt{2} p_1 p_2) \phi (q) = (q_{1}^2,q_{2}^2,\sqrt{2} q_1 q_2)\]

让我们定义一个核函数\(K(p,q)\)，它执行两个点之间的点积，如下所示

\[ \begin{aligned} K(p,q) = \phi(p).\phi(q) &= \phi(p)^T \phi(q) \\ &= (p_{1}^2,p_{2}^2,\sqrt{2} p_1 p_2).(q_{1}^2,q_{2}^2,\sqrt{2} q_1 q_2) \\ &= p_{1}^2 q_{1}^2 + p_{2}^2 q_{2}^2 + 2 p_1 q_1 p_2 q_2 \\ &= (p_1 q_1 + p_2 q_2)^2 \\ \phi(p).\phi(q) &= (p.q)^2 \end{aligned} \]

这意味着，三维空间中的点积可以用二维空间中的平方点积来实现。这可以应用于更高维的空间。所以我们可以从较低的维度计算较高的维度特征。一旦我们映射它们，我们就得到一个更高维的空间。

除了所有这些概念之外，还有一个误分类问题。因此，仅仅找到具有最大边距的决策边界是不够的。我们还需要考虑误分类错误的问题。有时，有可能找到边距较小的决策边界，但误分类较少。无论如何，我们需要修改我们的模型，使其应该找到具有最大边距但误分类较少的决策边界。最小化标准修改为

\[min \; ||w||^2 + C(误分类样本到其正确区域的距离)\]

下图显示了这个概念。对于训练数据的每个样本，定义一个新的参数\(\xi_i\)。它是其对应的训练样本到其正确决策区域的距离。对于那些没有被误分类的样本，它们落在其对应的支持平面上，因此它们的距离为零。

图像

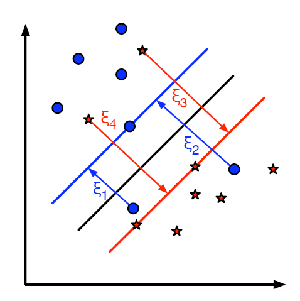
所以新的优化问题是

\[\min_{w, b_{0}} L(w,b_0) = ||w||^{2} + C \sum_{i} {\xi_{i}} \text{ 受限于 } y_{i}(w^{T} x_{i} + b_{0}) \geq 1 - \xi_{i} \text{ 且 } \xi_{i} \geq 0 \text{ } \forall i\]

参数C应该如何选择？很明显，这个问题的答案取决于训练数据是如何分布的。虽然没有普遍的答案，但考虑以下规则是有用的

C的大值给出误分类错误较少但边距较小的解。考虑在这种情况下，误分类错误的代价很高。由于优化的目的是最小化参数，因此允许很少的误分类错误。
C的小值给出边距较大但分类错误较多的解。在这种情况下，最小化并不那么考虑总和项，因此它更侧重于找到一个具有较大边距的超平面。

补充资源

NPTEL关于统计模式识别的笔记，第25-29章