目标

我们将了解光流的概念及其使用Lucas-Kanade方法进行估计。
我们将使用诸如cv.calcOpticalFlowPyrLK()之类的函数来跟踪视频中的特征点。

光流

光流是图像物体在两个连续帧之间表观运动的模式，是由物体或摄像机的运动引起的。它是一个二维向量场，其中每个向量都是一个位移向量，显示点从第一帧到第二帧的运动。请考虑下面的图像（图像来源：维基百科关于光流的文章）。

图像

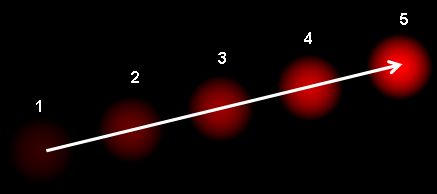
它显示了一个球在连续的5帧中移动。箭头显示其位移向量。光流在许多领域都有应用，例如

运动结构
视频压缩
视频稳定…

光流基于几个假设

对象的像素强度在连续帧之间不会改变。
相邻像素具有相似的运动。

考虑第一帧中的像素\(I(x,y,t)\)（注意这里添加了一个新的维度，时间。之前我们只处理图像，所以不需要时间）。它在\(dt\)时间后拍摄的下一帧中移动了\((dx,dy)\)的距离。由于这些像素是相同的并且强度没有改变，我们可以说，

\[I(x,y,t) = I(x+dx, y+dy, t+dt)\]

然后取右边的泰勒级数近似，去除公因式，并除以\(dt\)得到以下方程

\[f_x u + f_y v + f_t = 0 \;\]

其中

\[f_x = \frac{\partial f}{\partial x} \; ; \; f_y = \frac{\partial f}{\partial y}\]

\[u = \frac{dx}{dt} \; ; \; v = \frac{dy}{dt}\]

上述方程称为光流方程。其中，我们可以找到\(f_x\)和\(f_y\)，它们是图像梯度。同样，\(f_t\)是沿时间的梯度。但是\((u,v)\)是未知的。我们不能用一个方程来求解两个未知变量。因此，提供了几种方法来解决这个问题，其中一种是Lucas-Kanade方法。

Lucas-Kanade方法

我们之前看到一个假设，所有相邻像素都具有相似的运动。Lucas-Kanade方法在该点周围取一个3x3的块。因此，所有9个点都具有相同的运动。我们可以找到这9个点的\((f_x, f_y, f_t)\)。因此，现在我们的问题变成了用两个未知变量求解9个方程，这是一个超定问题。用最小二乘拟合法可以得到更好的解。以下是最终解，这是一个二元二次方程组，求解得到解。

\[\begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} \sum_{i}{f_{x_i}}^2 & \sum_{i}{f_{x_i} f_{y_i} } \\ \sum_{i}{f_{x_i} f_{y_i}} & \sum_{i}{f_{y_i}}^2 \end{bmatrix}^{-1} \begin{bmatrix} - \sum_{i}{f_{x_i} f_{t_i}} \\ - \sum_{i}{f_{y_i} f_{t_i}} \end{bmatrix}\]

（查看逆矩阵与Harris角点检测器的相似性。它表示角点是更好的跟踪点。）

因此，从用户的角度来看，这个想法很简单，我们给出一些要跟踪的点，我们接收这些点的光流向量。但是，仍然有一些问题。到目前为止，我们一直在处理小的运动。因此，当存在大的运动时，它会失败。所以我们再次使用金字塔。当我们向上移动金字塔时，小的运动被移除，大的运动变成小的运动。所以在那里应用Lucas-Kanade，我们得到光流以及比例。

OpenCV.js中的Lucas-Kanade光流

我们使用函数：cv.calcOpticalFlowPyrLK (prevImg, nextImg, prevPts, nextPts, status, err, winSize = new cv.Size(21, 21), maxLevel = 3, criteria = new cv.TermCriteria(cv.TermCriteria_COUNT+ cv.TermCriteria_EPS, 30, 0.01), flags = 0, minEigThreshold = 1e-4)。

参数

prevImg	第一个8位输入图像或由buildOpticalFlowPyramid构建的金字塔。
nextImg	第二个输入图像，大小和类型与prevImg相同。
prevPts	需要找到流的二维点向量；点坐标必须是单精度浮点数。
nextPts	包含在第二张图像中计算出的输入特征的新位置的二维点输出向量（具有单精度浮点坐标）；当传递cv.OPTFLOW_USE_INITIAL_FLOW标志时，向量的尺寸必须与输入中的相同。
status	输出状态向量（无符号字符）；如果已找到对应特征的流，则向量的每个元素设置为1，否则设置为0。
err	输出误差向量；向量的每个元素都设置为对应特征的误差，误差度量的类型可以在flags参数中设置；如果未找到流，则误差未定义（使用status参数查找此类情况）。
winSize	每个金字塔级别搜索窗口的大小。
maxLevel	基于0的最大金字塔级别编号；如果设置为0，则不使用金字塔（单级），如果设置为1，则使用两级，依此类推；如果金字塔传递到输入，则算法将使用与金字塔一样多的级别，但不超过maxLevel。
criteria	指定迭代搜索算法终止条件的参数（在指定的最大迭代次数criteria.maxCount之后或当搜索窗口移动小于criteria.epsilon时）。
flags	操作标志 cv.OPTFLOW_USE_INITIAL_FLOW 使用存储在nextPts中的初始估计；如果未设置该标志，则prevPts将被复制到nextPts并被视为初始估计。 cv.OPTFLOW_LK_GET_MIN_EIGENVALS 使用最小特征值作为误差度量（参见minEigThreshold描述）；如果未设置该标志，则使用原始点和移动点周围块之间的L1距离除以窗口中的像素数作为误差度量。
minEigThreshold	算法计算光流方程的2x2正规矩阵的最小特征值，除以窗口中的像素数；如果该值小于minEigThreshold，则过滤掉相应的特征，并且不处理其流，因此允许去除坏点并提高性能。

试一试

（此代码不检查下一个关键点的正确性。因此，即使任何特征点在图像中消失，光流也有可能找到下一个看起来接近它的点。因此，实际上，对于鲁棒的跟踪，应该在特定间隔内检测角点。）

OpenCV.js中的稠密光流

Lucas-Kanade 方法计算稀疏特征集的光流（在我们的例子中，使用 Shi-Tomasi 算法检测到的角点）。OpenCV.js 提供另一种算法来查找密集光流。它计算帧中所有点的光流。它基于 Gunnar Farneback 的算法，该算法在 Gunnar Farneback 2003 年的论文“基于多项式展开的两帧运动估计”中进行了解释。

我们使用函数：cv.calcOpticalFlowFarneback (prev, next, flow, pyrScale, levels, winsize, iterations, polyN, polySigma, flags)

参数

prev	第一个 8 位单通道输入图像。
next	第二个输入图像，大小和类型与 prev 相同。
flow	计算出的光流图像，大小与 prev 相同，类型为 CV_32FC2。
pyrScale	参数，指定为每个图像构建金字塔的图像比例（<1）；pyrScale=0.5 表示经典金字塔，其中每一层都比前一层小两倍。
levels	金字塔层数，包括初始图像；levels=1 表示不创建额外的层，只使用原始图像。
winsize	平均窗口大小；较大的值会增加算法对图像噪声的鲁棒性，并为快速运动检测提供更多机会，但会产生更模糊的运动场。
iterations	算法在每个金字塔级别上执行的迭代次数。
polyN	用于查找每个像素中多项式展开的像素邻域大小；较大的值意味着图像将使用更平滑的曲面进行近似，从而产生更鲁棒的算法和更模糊的运动场，通常 polyN =5 或 7。
polySigma	用于平滑用作多项式展开基础的导数的高斯函数的标准差；对于 polyN=5，可以设置 polySigma=1.1，对于 polyN=7，一个好的值是 polySigma=1.5。
flags	可以是以下组合的操作标志 cv.OPTFLOW_USE_INITIAL_FLOW 使用输入流作为初始流近似值。 cv.OPTFLOW_FARNEBACK_GAUSSIAN 使用高斯 𝚠𝚒𝚗𝚜𝚒𝚣𝚎×𝚠𝚒𝚗𝚜𝚒𝚣𝚎 滤波器代替相同大小的箱式滤波器进行光流估计；通常，此选项比使用箱式滤波器提供更精确的光流，但速度较慢；通常，高斯窗口的 winsize 应设置为较大的值以达到相同的鲁棒性水平。