轮廓特征

上一教程： 轮廓：入门
下一教程： 轮廓属性

目标

在本文中，我们将学习

• 查找轮廓的不同特征，例如面积、周长、质心、边界框等。
• 您将看到许多与轮廓相关的函数。

1. 矩

图像矩可以帮助您计算一些特征，例如物体的质心、物体的面积等。查看维基百科关于图像矩的页面。

函数cv.moments()给出一个包含所有计算出的矩值字典。见下文

import numpy as np
import cv2 as cv
 
img = cv.imread('star.jpg', cv.IMREAD_GRAYSCALE)
assert img is not None, "文件无法读取，请使用os.path.exists()检查"
ret,thresh = cv.threshold(img,127,255,0)
contours,hierarchy = cv.findContours(thresh, 1, 2)
 
cnt = contours[0]
M = cv.moments(cnt)
print( M )

从这些矩中，您可以提取有用的数据，例如面积、质心等。质心由关系给出，\(C_x = \frac{M_{10}}{M_{00}}\) 和 \(C_y = \frac{M_{01}}{M_{00}}\)。这可以按如下方式完成：

cx = int(M['m10']/M['m00'])
cy = int(M['m01']/M['m00'])

2. 轮廓面积

轮廓面积由函数cv.contourArea()或从矩M['m00']给出。

area = cv.contourArea(cnt)

3. 轮廓周长

它也称为弧长。可以使用cv.arcLength()函数找到它。第二个参数指定形状是封闭轮廓（如果传递True），还是只是一条曲线。

perimeter = cv.arcLength(cnt,True)

4. 轮廓逼近

它根据我们指定的精度将轮廓形状逼近到具有较少顶点的另一个形状。这是Douglas-Peucker算法的一种实现。查看维基百科页面以了解算法和演示。

要理解这一点，假设您正在尝试在图像中找到一个正方形，但是由于图像中的一些问题，您没有得到一个完美的正方形，而是一个“坏形状”（如下面的第一张图像所示）。现在您可以使用此函数来逼近形状。其中，第二个参数称为epsilon，它是轮廓到逼近轮廓的最大距离。这是一个精度参数。需要明智地选择epsilon才能获得正确的输出。

epsilon = 0.1*cv.arcLength(cnt,True)
approx = cv.approxPolyDP(cnt,epsilon,True)

下面，在第二张图像中，绿线显示了 epsilon 为弧长 10% 的近似曲线。第三张图像显示了 epsilon 为弧长 1% 的近似曲线。第三个参数指定曲线是闭合的还是非闭合的。

图像

5. 凸包

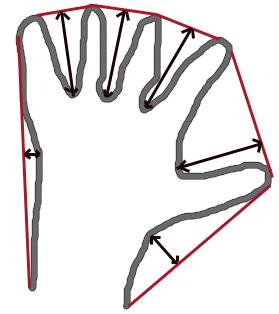
凸包看起来类似于轮廓逼近，但它并非如此（在某些情况下，两者可能提供相同的结果）。在这里，cv.convexHull()函数检查曲线的凸性缺陷并对其进行纠正。一般来说，凸曲线是总是凸出的曲线，或者至少是平坦的曲线。如果它向内凸出，则称为凸性缺陷。例如，检查下面手的图像。红线显示手的凸包。双向箭头表示凸性缺陷，它们是凸包与轮廓的局部最大偏差。

图像

关于它的语法，还有一些细节需要讨论

hull = cv.convexHull(points[, hull[, clockwise[, returnPoints]]])

参数详情

• points是我们传入的轮廓。
• hull是输出，通常我们避免使用它。
• clockwise：方向标志。如果为 True，则输出的凸包按顺时针方向定向。否则，则按逆时针方向定向。
• returnPoints：默认为 True。然后它返回凸包点的坐标。如果为 False，则返回对应于凸包点的轮廓点的索引。

因此，要获得如上图所示的凸包，以下就足够了：

hull = cv.convexHull(cnt)

但是，如果您想查找凸性缺陷，则需要将 returnPoints 设置为 False。为了理解它，我们将采用上面的矩形图像。首先，我将其轮廓找到为 cnt。现在，我使用 returnPoints = True 找到了它的凸包，我得到了以下值：[[[234 202]], [[ 51 202]], [[ 51 79]], [[234 79]]]，它们是矩形的四个角点。现在，如果使用 returnPoints = False 执行相同的操作，我将得到以下结果：[[129],[ 67],[ 0],[142]]。这些是轮廓中相应点的索引。例如，检查第一个值：cnt[129] = [[234, 202]]，它与第一个结果相同（其他结果也是如此）。

在讨论凸性缺陷时，我们将再次看到它。

6. 检查凸性

有一个函数可以检查曲线是否为凸的，cv.isContourConvex()。它只返回 True 或 False。没什么大不了的。

k = cv.isContourConvex(cnt)

7. 边界矩形

有两种类型的边界矩形。

7.a. 直边界矩形

这是一个直矩形，不考虑物体的旋转。因此，边界矩形的面积不会最小。它由函数cv.boundingRect()找到。

设(x,y)为矩形的左上角坐标，(w,h)为其宽度和高度。

x,y,w,h = cv.boundingRect(cnt)
cv.rectangle(img,(x,y),(x+w,y+h),(0,255,0),2)

7.b. 旋转矩形

这里，边界矩形以最小面积绘制，因此它也考虑了旋转。使用的函数是cv.minAreaRect()。它返回一个Box2D结构，其中包含以下详细信息 - (中心(x,y)，(宽度，高度)，旋转角度)。但要绘制此矩形，我们需要矩形的4个角点。它由函数cv.boxPoints()获得

rect = cv.minAreaRect(cnt)
box = cv.boxPoints(rect)
box = np.int0(box)
cv.drawContours(img,[box],0,(0,0,255),2)

两个矩形都显示在同一图像中。绿色矩形显示普通边界矩形。红色矩形是旋转矩形。

图像

8. 最小外接圆

接下来，我们使用函数cv.minEnclosingCircle()查找对象的圆周。它是一个完全覆盖具有最小面积的对象的圆。

(x,y),radius = cv.minEnclosingCircle(cnt)
center = (int(x),int(y))
radius = int(radius)
cv.circle(img,center,radius,(0,255,0),2)

9. 拟合椭圆

下一个是将椭圆拟合到物体上。它返回椭圆内切的旋转矩形。

ellipse = cv.fitEllipse(cnt)
cv.ellipse(img,ellipse,(0,255,0),2)

10. 拟合直线

类似地，我们可以将一条直线拟合到一组点。下图包含一组白点。我们可以用一条直线来近似它。

rows,cols = img.shape[:2]
[vx,vy,x,y] = cv.fitLine(cnt, cv.DIST_L2,0,0.01,0.01)
lefty = int((-x*vy/vx) + y)
righty = int(((cols-x)*vy/vx)+y)
cv.line(img,(cols-1,righty),(0,lefty),(0,255,0),2)