OpenCV 中的 K-Means 聚类

目标

• 学习使用 OpenCV 中的 cv.kmeans() 函数进行数据聚类

理解参数

输入参数

1. samples：它应该是 np.float32 数据类型，并且每个特征应该放在一个单独的列中。
2. nclusters(K)：最终需要的簇的数量
3. criteria：这是迭代终止条件。当满足此条件时，算法迭代停止。实际上，它应该是一个包含 3 个参数的元组。它们是 `( type, max_iter, epsilon )`
   1. 终止条件的类型。它有 3 个标志如下
      • cv.TERM_CRITERIA_EPS - 如果达到指定的精度 epsilon，则停止算法迭代。
      • cv.TERM_CRITERIA_MAX_ITER - 在指定的迭代次数 max_iter 后停止算法。
      • cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER - 当满足上述任何条件时停止迭代。
   2. max_iter - 指定最大迭代次数的整数。
   3. epsilon - 要求的精度
4. attempts：标志，用于指定使用不同初始标签执行算法的次数。算法返回产生最佳紧凑性的标签。此紧凑性作为输出返回。
5. flags：此标志用于指定如何获取初始中心。通常使用两个标志：cv.KMEANS_PP_CENTERS 和 cv.KMEANS_RANDOM_CENTERS。

输出参数

1. compactness：它是每个点到其对应中心的平方距离之和。
2. labels：这是标签数组（与之前文章中的“code”相同），其中每个元素标记为“0”，“1”......
3. centers：这是簇的中心数组。

现在我们将看到如何通过三个示例应用 K-Means 算法。

1. 只有单特征的数据

假设您有一组数据，只有一个特征，即一维的。例如，我们可以采用我们的 T 恤问题，其中您仅使用人的身高来确定 T 恤的尺寸。

因此，我们首先创建数据并在 Matplotlib 中绘制它

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt
 
x = np.random.randint(25,100,25)
y = np.random.randint(175,255,25)
z = np.hstack((x,y))
z = z.reshape((50,1))
z = np.float32(z)
plt.hist(z,256,[0,256]),plt.show()

因此，我们有 'z'，它是一个大小为 50 的数组，值范围从 0 到 255。我将 'z' 重塑为一个列向量。当存在多个特征时，它会更有用。然后我创建了 np.float32 类型的数据。

我们得到以下图像

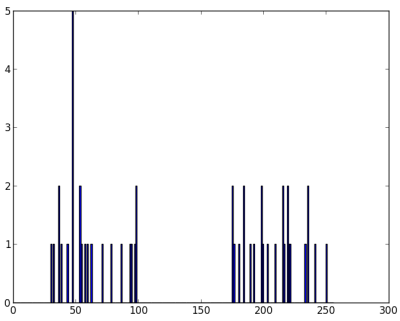
image

现在我们应用 KMeans 函数。在此之前，我们需要指定标准。我的标准是，无论何时运行算法的 10 次迭代，或达到 epsilon = 1.0 的精度，停止该算法并返回答案。

# 定义 criteria = ( type, max_iter = 10 , epsilon = 1.0 )
criteria = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 10, 1.0)
 
# 设置标志（只是为了避免代码中的换行符）
flags = cv.KMEANS_RANDOM_CENTERS
 
# 应用 KMeans
compactness,labels,centers = cv.kmeans(z,2,None,criteria,10,flags)

这给了我们紧凑性、标签和中心。在这种情况下，我得到的中心为 60 和 207。标签将具有与测试数据相同的大小，其中每个数据将被标记为“0”、“1”、“2”等，具体取决于它们的质心。现在我们根据它们的标签将数据分成不同的簇。

A = z[labels==0]
B = z[labels==1]

现在我们用红色绘制 A，用蓝色绘制 B，并用黄色绘制它们的质心。

# 现在用红色绘制“A”，用蓝色绘制“B”，用黄色绘制“中心”
plt.hist(A,256,[0,256],color = 'r')
plt.hist(B,256,[0,256],color = 'b')
plt.hist(centers,32,[0,256],color = 'y')
plt.show()

下面是我们得到的输出

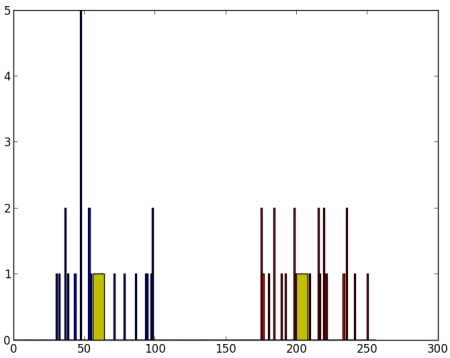
image

2. 具有多个特征的数据

在前面的示例中，我们只考虑了 T 恤问题的身高。在这里，我们将同时考虑身高和体重，即两个特征。

请记住，在前面的示例中，我们将数据制成一个单列向量。每个特征都排列在一列中，而每一行对应于一个输入测试样本。

例如，在这种情况下，我们设置了一个大小为 50x2 的测试数据，这些是 50 个人的身高和体重。第一列对应于所有 50 个人的身高，第二列对应于他们的体重。第一行包含两个元素，其中第一个是第一个人的身高，第二个是他的体重。类似地，其余行对应于其他人的身高和体重。检查下面的图片

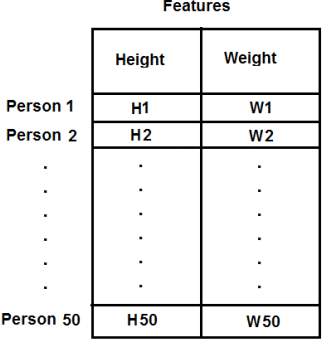
image

现在我直接转到代码

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt
 
X = np.random.randint(25,50,(25,2))
Y = np.random.randint(60,85,(25,2))
Z = np.vstack((X,Y))
 
# 转换为 np.float32
Z = np.float32(Z)
 
# 定义标准并应用 kmeans()
criteria = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 10, 1.0)
ret,label,center=cv.kmeans(Z,2,None,criteria,10,cv.KMEANS_RANDOM_CENTERS)
 
# 现在分离数据，注意 flatten()
A = Z[label.ravel()==0]
B = Z[label.ravel()==1]
 
# 绘制数据
plt.scatter(A[:,0],A[:,1])
plt.scatter(B[:,0],B[:,1],c = 'r')
plt.scatter(center[:,0],center[:,1],s = 80,c = 'y', marker = 's')
plt.xlabel('Height'),plt.ylabel('Weight')
plt.show()

下面是我们得到的输出

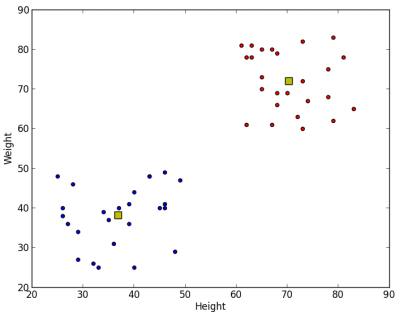
image

3. 颜色量化

颜色量化是减少图像中颜色数量的过程。这样做的一个原因是减少内存。有时，某些设备可能有限制，以至于它只能产生有限数量的颜色。在这些情况下，也会执行颜色量化。在这里，我们使用 k-means 聚类进行颜色量化。

这里没有什么新的需要解释。有 3 个特征，例如 R、G、B。因此，我们需要将图像重塑为 Mx3 大小的数组（M 是图像中的像素数）。聚类后，我们将质心值（它也是 R、G、B）应用于所有像素，这样生成的图像将具有指定的颜色数。我们需要再次将其重塑回原始图像的形状。下面是代码

import numpy as np
import cv2 as cv
 
img = cv.imread('home.jpg')
Z = img.reshape((-1,3))
 
# 转换为 np.float32
Z = np.float32(Z)
 
# 定义标准，簇数 (K) 并应用 kmeans()
criteria = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 10, 1.0)
K = 8
ret,label,center=cv.kmeans(Z,K,None,criteria,10,cv.KMEANS_RANDOM_CENTERS)
 
# 现在转换回 uint8 并制作原始图像
center = np.uint8(center)
res = center[label.flatten()]
res2 = res.reshape((img.shape))
 
cv.imshow('res2',res2)
cv.waitKey(0)
cv.destroyAllWindows()

请参见下面的 K=8 的结果

image