 |
OpenCV 4.12.0
开源计算机视觉
|
 |
OpenCV 4.12.0
开源计算机视觉
|
在本章中
考虑下图,它有两种类型的数据,红色和蓝色。在 kNN 中,对于测试数据,我们过去衡量它到所有训练样本的距离,并取距离最小的样本。这需要大量时间来衡量所有距离,并需要大量内存来存储所有训练样本。但是考虑到图像中给出的数据,我们需要那么多吗?
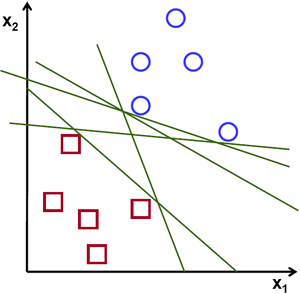
考虑另一个想法。我们找到一条直线,\(f(x)=ax_1+bx_2+c\) 将两个数据分成两个区域。当我们得到一个新的 test_data \(X\) 时,只需将其代入 \(f(x)\) 中。如果 \(f(X) > 0\),则它属于蓝色组,否则属于红色组。我们可以称这条线为决策边界。它非常简单且节省内存。可以用直线(或更高维度中的超平面)分成两部分的数据称为线性可分。
所以在上图中,你可以看到很多这样的线都是可能的。我们将选择哪一条?凭直觉,我们可以说这条线应该尽可能远离所有点。为什么?因为传入的数据中可能存在噪声。此数据不应影响分类精度。因此,选择最远的线将提供更大的抗噪声能力。因此,SVM 的作用是找到一条直线(或超平面),使其到训练样本的最小距离最大。请参阅下图穿过中心的粗体线。
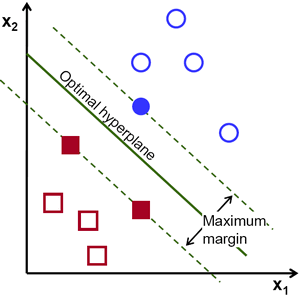
因此,要找到此决策边界,您需要训练数据。你需要所有数据吗?不需要。只需要那些靠近相反组的数据就足够了。在我们的图像中,它们是一个蓝色的填充圆圈和两个红色的填充正方形。我们可以称它们为支持向量,而穿过它们的线称为支持平面。它们足以找到我们的决策边界。我们不必担心所有数据。它有助于数据缩减。
发生的情况是,首先找到两个最能代表数据的超平面。例如,蓝色数据由 \(w^Tx+b_0 > 1\) 表示,而红色数据由 \(w^Tx+b_0 < -1\) 表示,其中 \(w\) 是权重向量 ( \(w=[w_1, w_2,..., w_n]\)),\(x\) 是特征向量 ( \(x = [x_1,x_2,..., x_n]\))。\ (b_0\) 是偏差。权重向量决定决策边界的方向,而偏差点决定其位置。现在,决策边界被定义为这些超平面之间的中间位置,因此表示为 \(w^Tx+b_0 = 0\)。从支持向量到决策边界的最小距离由 \(distance_{support \, vectors}=\frac{1}{||w||}\) 给出。裕量是此距离的两倍,我们需要最大化此裕量。即,我们需要最小化一个新函数 \(L(w, b_0)\),该函数具有一些约束,如下所示
\[\min_{w, b_0} L(w, b_0) = \frac{1}{2}||w||^2 \; \text{限制为} \; t_i(w^Tx+b_0) \geq 1 \; \forall i\]
其中 \(t_i\) 是每个类的标签,\(t_i \in [-1,1]\)。
考虑一些无法用直线分成两部分的数据。例如,考虑一个一维数据,其中 'X' 位于 -3 & +3,而 'O' 位于 -1 & +1。显然,它是非线性可分的。但是有一些方法可以解决这些类型的问题。如果我们能用一个函数 \(f(x) = x^2\) 映射这个数据集,我们就会得到 'X' 在 9 和 'O' 在 1,它们是线性可分的。
否则,我们可以将此一维数据转换为二维数据。我们可以使用 \(f(x)=(x,x^2)\) 函数来映射此数据。然后,'X' 变为 (-3,9) 和 (3,9),而 'O' 变为 (-1,1) 和 (1,1)。这也是线性可分的。简而言之,非线性可分数据在较低维空间中更可能变成较高维空间中的线性可分数据。
一般来说,可以将 d 维空间中的点映射到某个 D 维空间 \((D>d)\) 以检查线性可分性的可能性。有一种想法有助于通过在低维输入(特征)空间中执行计算来计算高维(内核)空间中的点积。我们可以用以下示例来说明。
考虑二维空间中的两个点,\(p=(p_1,p_2)\) 和 \(q=(q_1,q_2)\)。设 \(\phi\) 是一个映射函数,它将二维点映射到三维空间,如下所示
\[\phi (p) = (p_{1}^2,p_{2}^2,\sqrt{2} p_1 p_2) \phi (q) = (q_{1}^2,q_{2}^2,\sqrt{2} q_1 q_2)\]
让我们定义一个内核函数 \(K(p,q)\),它在两个点之间执行点积,如下所示
\[ \begin{aligned} K(p,q) = \phi(p).\phi(q) &= \phi(p)^T \phi(q) \\ &= (p_{1}^2,p_{2}^2,\sqrt{2} p_1 p_2).(q_{1}^2,q_{2}^2,\sqrt{2} q_1 q_2) \\ &= p_{1}^2 q_{1}^2 + p_{2}^2 q_{2}^2 + 2 p_1 q_1 p_2 q_2 \\ &= (p_1 q_1 + p_2 q_2)^2 \\ \phi(p).\phi(q) &= (p.q)^2 \end{aligned} \]
这意味着,可以使用二维空间中的平方点积来实现三维空间中的点积。这可以应用于更高维的空间。因此,我们可以从较低维度本身计算较高维度的特征。一旦我们映射它们,我们就会得到一个较高维的空间。
除了所有这些概念之外,还出现了错误分类的问题。因此,仅仅找到具有最大裕量的决策边界是不够的。我们还需要考虑错误分类的错误问题。有时,可能可以找到具有较小裕量的决策边界,但错误分类减少了。无论如何,我们需要修改我们的模型,使其找到具有最大裕量的决策边界,但错误分类较少。最小化标准修改为
\[min \; ||w||^2 + C(误分类样本到其正确区域的距离)\]
下图显示了此概念。对于训练数据的每个样本,都会定义一个新参数 \(\xi_i\)。它是从其对应的训练样本到其正确决策区域的距离。对于那些未被错误分类的人,它们落在其对应的支持平面上,因此它们的距离为零。
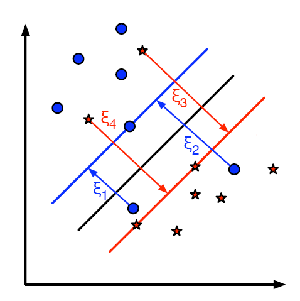
因此,新的优化问题是
\[\min_{w, b_{0}} L(w,b_0) = ||w||^{2} + C \sum_{i} {\xi_{i}} \text{ 限制为 } y_{i}(w^{T} x_{i} + b_{0}) \geq 1 - \xi_{i} \text{ 且 } \xi_{i} \geq 0 \text{ } \forall i\]
应如何选择参数 C?很明显,这个问题的答案取决于训练数据的分布方式。虽然没有通用的答案,但考虑这些规则是有用的