理解 k 近邻

目标

在本章中，我们将理解 k 近邻（kNN）算法的概念。

理论

kNN 是可用于监督学习的最简单的分类算法之一。 其思想是在特征空间中搜索测试数据的最接近匹配项。 我们将通过下图来研究它。

image

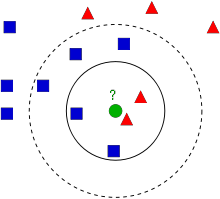
在图中，有两个家族：蓝色正方形和红色三角形。 我们将每个家族称为一个类。 他们的房屋显示在他们的城镇地图中，我们将其称为特征空间。 您可以将特征空间视为所有数据都被投影的空间。 例如，考虑一个 2D 坐标空间。 每个数据都有两个特征，一个 x 坐标和一个 y 坐标。 您可以在 2D 坐标空间中表示此数据，对吗？ 现在想象一下有三个特征，您将需要 3D 空间。 现在考虑 N 个特征：您需要 N 维空间，对吗？ 这个 N 维空间就是它的特征空间。 在我们的图像中，您可以将其视为具有两个特征的 2D 案例。

现在考虑一下如果一个新成员来到镇上并创建了一个新家，即图中所示的绿色圆圈，会发生什么。 他应该被添加到这些蓝色或红色家族（或类）之一。 我们称该过程为分类。 应该如何对这位新成员进行分类呢？ 由于我们正在处理 kNN，让我们应用该算法。

一种简单的方法是检查谁是他最近的邻居。 从图像中可以清楚地看出，它是红色三角形家族的成员。 因此，他被归类为红色三角形。 这种方法简称为最近邻分类，因为分类仅取决于最近邻。

但是这种方法存在问题！ 红色三角形可能是最近的邻居，但是如果附近也有很多蓝色正方形怎么办？ 那么蓝色正方形在该地区的强度高于红色三角形，因此仅检查最近的一个是不够的。 相反，我们可能需要检查一些k个最近的家族。 然后，无论哪个家族在其中占多数，新成员都应该属于该家族。 在我们的图像中，让我们取 k=3，即考虑 3 个最近的邻居。 新成员有两个红色邻居和一个蓝色邻居（有两个蓝色等距，但是由于 k=3，我们只能取其中一个），因此他应该再次被添加到红色家族。 但是如果我们取 k=7 呢？ 那么他有 5 个蓝色邻居和 2 个红色邻居，应该被添加到蓝色家族。 结果会随着 k 的选择值而变化。 请注意，如果 k 不是奇数，我们可能会得到一个平局，就像上面的 k=4 的情况一样。 我们会看到，作为他最近的四个邻居，我们的新成员有 2 个红色邻居和 2 个蓝色邻居，我们需要选择一种打破平局的方法来进行分类。 因此，重申一下，此方法称为 k 近邻，因为分类取决于k 个最近的邻居。

同样，在 kNN 中，确实我们正在考虑 k 个邻居，但是我们对所有邻居都给予了同等的重要性，对吗？ 这合理吗？ 例如，考虑 k=4 的平局情况。 正如我们所看到的，与另外 2 个蓝色邻居相比，2 个红色邻居实际上更靠近新成员，因此他更有资格被添加到红色家族。 我们如何在数学上解释这一点？ 我们根据每个邻居与新来者的距离为每个邻居赋予一定的权重：离他较近的邻居获得较高的权重，而离他较远的邻居获得较低的权重。 然后，我们分别将每个家族的总权重相加，并将新来者归类为获得较高总权重家族的一部分。 这称为改进的 kNN 或加权 kNN。

那么您在这里看到哪些重要的事情？

• 因为我们必须检查新来者与所有现有房屋之间的距离才能找到最近的邻居，所以您需要掌握城镇中所有房屋的信息，对吗？ 如果有很多房屋和家庭，则会占用大量内存，并且计算时间也会更长。
• 对于任何类型的“训练”或准备，几乎没有时间。 我们的“学习”仅涉及在测试和分类之前记忆（存储）数据。

现在让我们看看这种算法在 OpenCV 中的工作方式。

OpenCV 中的 kNN

我们将在这里做一个简单的示例，就像上面一样，有两个家族（类）。 然后在下一章中，我们将做一个更好的示例。

因此，在这里，我们将红色家族标记为类-0（因此用 0 表示），将蓝色家族标记为类-1（用 1 表示）。 我们创建 25 个邻居或 25 个训练数据，并将每个邻居标记为类-0 或类-1 的一部分。 我们可以借助 NumPy 中的随机数生成器来做到这一点。

然后，我们可以借助 Matplotlib 绘制它。 红色邻居显示为红色三角形，蓝色邻居显示为蓝色正方形。

import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt
 
# 包含 25 个已知/训练数据的 (x,y) 值的特征集
trainData = np.random.randint(0,100,(25,2)).astype(np.float32)
 
# 使用数字 0 和 1 将每个邻居标记为红色或蓝色
responses = np.random.randint(0,2,(25,1)).astype(np.float32)
 
# 获取红色邻居并绘制它们
red = trainData[responses.ravel()==0]
plt.scatter(red[:,0],red[:,1],80,'r','^')
 
# 获取蓝色邻居并绘制它们
blue = trainData[responses.ravel()==1]
plt.scatter(blue[:,0],blue[:,1],80,'b','s')
 
plt.show()

您将获得类似于我们第一张图像的内容。 由于您使用的是随机数生成器，因此每次运行代码都会获得不同的数据。

接下来，启动 kNN 算法并将 trainData 和 responses 传递给 kNN 进行训练。 （在底层，它构建了一个搜索树：有关此问题的更多信息，请参见下面的“其他资源”部分。）

然后，我们将带来一位新来者，并在 OpenCV 中借助 kNN 将其分类为属于一个家族。 在运行 kNN 之前，我们需要了解一些关于我们的测试数据（新来者的数据）的信息。 我们的数据应该是一个浮点数组，大小为 \(测试数据数量 \; \times 特征数量\)。 然后，我们找到新来者的最近邻居。 我们可以指定k：我们想要多少个邻居。 （这里我们使用了 3 个。） 它返回

1. 根据我们之前看到的 kNN 理论，给予新来者的标签。 如果您想要最近邻算法，只需指定 k=1。
2. k 个最近邻居的标签。
3. 从新来者到每个最近邻居的相应距离。

让我们看看它是如何工作的。 新来者用绿色标记。

newcomer = np.random.randint(0,100,(1,2)).astype(np.float32)
plt.scatter(newcomer[:,0],newcomer[:,1],80,'g','o')
 
knn = cv.ml.KNearest_create()
knn.train(trainData, cv.ml.ROW_SAMPLE, responses)
ret, results, neighbours ,dist = knn.findNearest(newcomer, 3)
 
print( "结果: {}\n".format(results) )
print( "邻居: {}\n".format(neighbours) )
print( "距离: {}\n".format(dist) )
 
plt.show()

我得到了以下结果

结果: [[ 1.]]
邻居: [[ 1. 1. 1.]]
距离: [[ 53. 58. 61.]]

它说我们新来者的 3 个最近邻居都来自蓝色家族。 因此，他被标记为蓝色家族的一部分。 从下面的图中可以明显看出

image

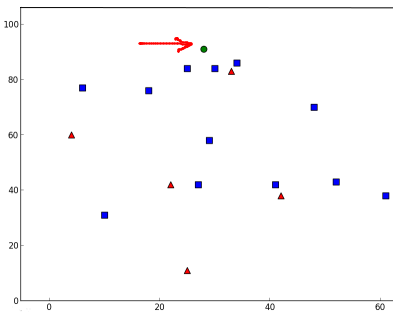
如果您有多个新来者（测试数据），则只需将它们作为数组传递。 相应的結果也会作为数组获得。

# 10 个新来者
newcomers = np.random.randint(0,100,(10,2)).astype(np.float32)
ret, results,neighbours,dist = knn.findNearest(newcomer, 3)
# 结果还将包含 10 个标签。

其他资源

1. NPTEL 关于模式识别的笔记，第 11 章
2. 关于最近邻搜索的维基百科文章
3. 关于 k-d 树的维基百科文章

练习

1. 尝试使用更多的类和不同的 k 值重复上述操作。 在同一个 2D 特征空间中，随着类的增多，选择 k 是否变得更加困难？