霍夫线变换

目标

在本章中，

• 我们将理解霍夫变换的概念。
• 我们将学习如何使用它来检测图像中的线条。
• 我们将学习以下函数：cv.HoughLines(), cv.HoughLinesP()

理论

如果您可以用数学形式表示任何形状，那么霍夫变换是一种检测该形状的流行技术。即使形状被破坏或稍微变形，它也可以检测到该形状。我们将看到它如何用于直线。

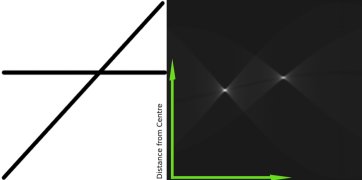
一条直线可以表示为 \(y = mx+c\) 或参数形式，如 \(\rho = x \cos \theta + y \sin \theta\)，其中 \(\rho\) 是从原点到该线的垂直距离，\(\theta\) 是这条垂直线与水平轴逆时针方向形成的夹角（该方向取决于您如何表示坐标系。此表示法在 OpenCV 中使用）。查看下面的图像

image

因此，如果直线经过原点下方，它将具有正的 rho 和小于 180 的角度。如果它经过原点上方，则角度将小于 180 而不是大于 180，并且 rho 将为负。任何垂直线都将具有 0 度，水平线将具有 90 度。

现在让我们看看霍夫变换是如何用于直线的。任何直线都可以用这两个参数 \(\rho, \theta\) 表示。因此，它首先创建一个 2D 数组或累加器（用于保存两个参数的值），并将其初始设置为 0。让行表示 \(\rho\)，列表示 \(\theta\)。数组的大小取决于您需要的精度。假设您希望角度的精度为 1 度，则需要 180 列。对于 \(\rho\)，可能的最大距离是图像的对角线长度。因此，以一个像素的精度，行数可以是图像的对角线长度。

考虑一个 100x100 的图像，中间有一条水平线。取该线的第一个点。您知道它的 (x,y) 值。现在在直线方程中，输入值 \(\theta = 0,1,2,....,180\) 并检查得到的 \(\rho\)。对于每一对 \((\rho, \theta)\)，在累加器中其对应的 \((\rho, \theta)\) 单元格中将值加一。因此，现在在累加器中，单元格 (50,90) = 1 以及一些其他单元格。

现在取直线上的第二个点。执行与上面相同的操作。增加与您获得的 (rho, theta) 对应的单元格中的值。这一次，单元格 (50,90) = 2。您实际所做的是对 \((\rho, \theta)\) 值进行投票。您对直线上的每个点都继续此过程。在每个点，单元格 (50,90) 将被递增或投票增加，而其他单元格可能会或可能不会被投票增加。这样，最后，单元格 (50,90) 将具有最大票数。因此，如果您在累加器中搜索最大票数，您将获得值 (50,90)，它表示在此图像中有一条线，距离原点 50，角度为 90 度。它在下面的动画中很好地显示出来（图像来源：Amos Storkey）

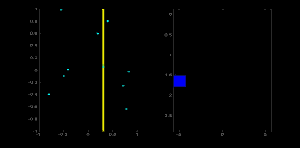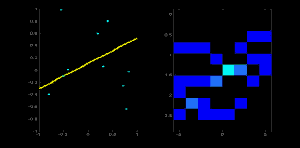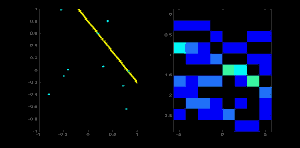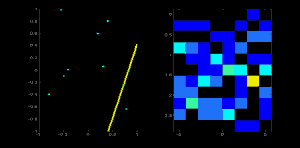
这就是霍夫变换如何用于直线。它很简单，也许您可以使用 Numpy 自己实现它。下面是一个显示累加器的图像。某些位置的亮点表示它们是图像中可能直线的参数。（图片来源：维基百科）

OpenCV 中的霍夫变换

上面解释的所有内容都封装在 OpenCV 函数 cv.HoughLines() 中。它只是返回一个 :math:(rho, theta)` 值的数组。\(\rho\) 以像素为单位测量，\(\theta\) 以弧度为单位测量。第一个参数，输入图像应该是二值图像，所以在应用霍夫变换之前应用阈值或使用 canny 边缘检测。第二和第三个参数分别是 \(\rho\) 和 \(\theta\) 精度。第四个参数是阈值，这意味着它应该获得的最小票数才能被视为一条直线。请记住，票数取决于直线上的点数。因此，它表示应该检测到的最小直线长度。

import cv2 as cv
import numpy as np
 
img = cv.imread(cv.samples.findFile('sudoku.png'))
gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)
edges = cv.Canny(gray,50,150,apertureSize = 3)
 
lines = cv.HoughLines(edges,1,np.pi/180,200)
for line in lines
rho,theta = line[0]
a = np.cos(theta)
b = np.sin(theta)
x0 = a*rho
y0 = b*rho
x1 = int(x0 + 1000*(-b))
y1 = int(y0 + 1000*(a))
x2 = int(x0 - 1000*(-b))
y2 = int(y0 - 1000*(a))
 
    cv.line(img,(x1,y1),(x2,y2),(0,0,255),2)
 
cv.imwrite('houghlines3.jpg',img)

查看下面的结果

image

概率霍夫变换

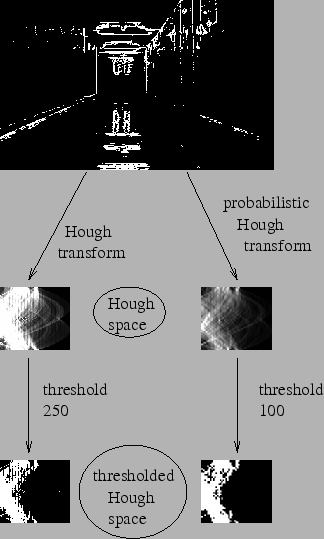
在霍夫变换中，您可以看到即使对于具有两个参数的直线，也需要大量的计算。概率霍夫变换是我们看到的霍夫变换的优化。它不考虑所有点。相反，它只取随机点的子集，这些点足以进行线检测。我们只需要降低阈值。查看下面的图像，它比较了霍夫空间中的霍夫变换和概率霍夫变换。（图片来源：Franck Bettinger 的主页）

image

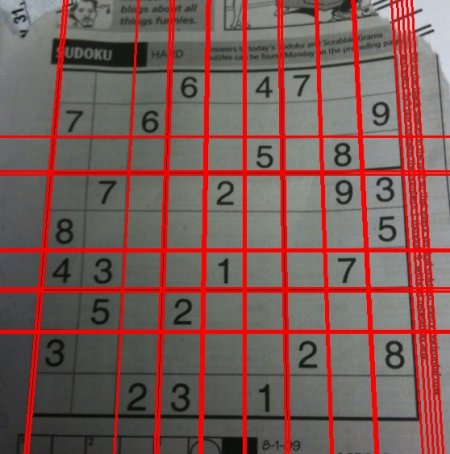
OpenCV 实现基于 Matas, J. 和 Galambos, C. 和 Kittler, J.V. 的使用渐进概率霍夫变换进行鲁棒直线检测 [188]。使用的函数是 cv.HoughLinesP()。它有两个新参数。

• minLineLength - 线段的最小长度。短于此值的线段将被拒绝。
• maxLineGap - 被视为单条线的线段之间的最大允许间隙。

最好的事情是，它直接返回线的两个端点。在前面的例子中，您只得到了直线的参数，并且必须找到所有的点。在这里，一切都是直接而简单的。

import cv2 as cv
import numpy as np
 
img = cv.imread(cv.samples.findFile('sudoku.png'))
gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)
edges = cv.Canny(gray,50,150,apertureSize = 3)
lines = cv.HoughLinesP(edges,1,np.pi/180,100,minLineLength=100,maxLineGap=10)
for line in lines
x1,y1,x2,y2 = line[0]
    cv.line(img,(x1,y1),(x2,y2),(0,255,0),2)
 
cv.imwrite('houghlines5.jpg',img)

查看下面的结果

image

补充资源

1. 维基百科上的霍夫变换