 |
OpenCV 4.12.0
开源计算机视觉
|
 |
OpenCV 4.12.0
开源计算机视觉
|
在本教程中,将介绍模糊变换的基本概念。您将学习
所提供的解释需要具备基本的数学知识。所有相关的论文都被引用,并且大多数可以在 https://www.researchgate.net/ 上访问。
近年来,F-变换的理论在许多方向上得到了深入发展。在图像处理中,它已成功应用于图像压缩和缩减、图像融合、边缘检测和图像重建 [222] [71] [284] [220] [219] [290]。 F-变换是一种将连续/离散函数与其 F-变换分量的有限向量对应的技术。在图像处理中,图像由两个参数的强度函数标识,后者的 F-变换由分量矩阵给出。
让我介绍一下二维灰度图像 \(I\) 的 F-变换,该图像被视为函数 \(I:[0,M]\times [0,N]\to [0,255]\),其中 \([0,M]=\{0,1,2,\ldots,M\}; [0,N]=\{0,1,2,\ldots,N\}\)。假设图像定义在属于集合 \(P\) 的点(像素)上,其中 \(P=\{(x,y)\mid x=0,1,\ldots, M;y=0,1,\ldots, N\}\)。
设 \(A_0, \dots ,A_m\) 和 \(B_0, \dots ,B_n\) 为基本函数,\(A_0, \dots ,A_m : [0,M] \to [0, 1]\) 为 \([0,M]\) 的模糊划分,\(B_0, \dots ,B_n :[0,N]\to [0, 1]\) 为 \([0,N]\) 的模糊划分。假设像素集 \(P\) 对于所选择的划分来说足够密集。这意味着对于所有 \(k\in{0,\dots, m}(\exists x\in [0,M]) \ A_k(x)>0\),并且对于所有 \(l\in{0,\dots, n}(\exists y\in [0,N])\ B_l(y)>0\)。
\(F^0\)
我们说实数 \(m\times n\) 矩阵 \(F^0_{mn}[I] = (F^0_{kl})\) 称为 \(I\) 相对于 \(\{A_0, \dots,A_m\}\) 和 \(\{B_0, \dots,B_n\}\) 的(离散)F-变换,如果对于所有 \(k=0,\dots,m,\ l=0,\dots,n\)
\[ F^0_{kl}=\frac{\sum_{y=0}^{N}\sum_{x=0}^{M} I(x,y)A_k(x)B_l(y)}{\sum_{y=0}^{N}\sum_{x=0}^{M} A_k(x)B_l(y)}. \]
系数 \(F^0_{kl}\) 称为 \(F^0\)-变换的分量。
\(F^1\)
\(F^1\)-变换已在 [221] 中介绍。我们说矩阵 \(F^1_{mn}[I] = (F^1_{kl}), k=0,\ldots, m, l=0,\ldots, n\) 是 \(I\) 相对于 \(\{A_k\times B_l\mid k=0,\ldots, m, l=0,\ldots, n\}\) 的 \(F^1\)-变换,\(F^1_{kl}\) 是相应的 \(F^1\)-变换分量。
\(I\) 的 \(F^1\)-变换分量是以下形式的线性多项式
\[ F^1_{kl}(x,y)= c^{00}_{kl} + c^{10}_{kl}(x-x_k) + c^{01}_{kl}(y-y_l), \]
其中系数由下式给出
\[ c_{kl}^{00} =\frac{\sum_{y=0}^{N}\sum_{x=0}^{M} I(x,y)A_k(x)B_l(y)}{\sum_{y=0}^{N}\sum_{x=0}^{M} A_k(x)B_l(y)}, \\ c_{kl}^{10} =\frac{\sum_{y=0}^{N}\sum_{x=0}^{M} I(x,y)(x - x_k)A_k(x)B_l(y)}{\sum_{y=0}^{N}\sum_{x=0}^{M} (x - x_k)^2A_k(x)B_l(y)}, \\ c_{kl}^{01} =\frac{\sum_{y=0}^{N}\sum_{x=0}^{M} I(x,y)(y - y_l)A_k(x)B_l(y)}{\sum_{y=0}^{N}\sum_{x=0}^{M} (y - y_l)^2A_k(x)B_l(y)}. \]
F-变换技术使用两个步骤:直接和逆。直接步骤在上一节中描述,而逆步骤如下
\[ O(x,y)=\sum_{k=0}^{m}\sum_{l=0}^{n} F^d_{kl}A_k(x)B_l(y), \]
其中 \(O\) 是输出(重建)图像,\(d\) 是 F-变换的阶数。 实际上,该算法计算输入图像 \(I\) 的 F-变换分量,然后将这些分量扩展到 \(I\) 的大小。 有关详细信息,请参见 [219]。 可以从两个不同的角度进行图像处理应用。
像素一个接一个地被处理,以便为每个像素找到适当的基本函数。 每个方向上将恰好有四个。 我们需要在内存中存储一些辅助结构,以收集它们的值。 这些值将用于相关模糊分量的分子中。 这种方法的实现使用关键字 FL 作为快速处理(由于更多的优化)和线性基本函数。
通过这种方式,图像被划分为规则区域。 使用内核窗口分别处理每个区域。 这种方法受益于易于理解的,基于矩阵的处理以及直接的并行化。
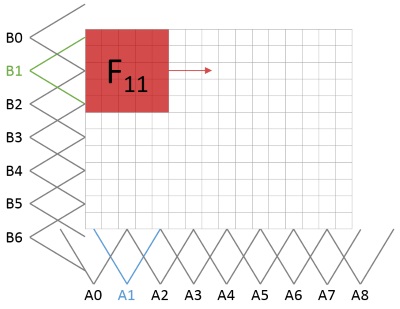
这种方法使用内核 \(g\)。 让我们以半径 \(h = 2\) 的线性情况为例。
\[ A = (0, 0.5, 1, 0.5, 0) \\ B^T = (0, 0.5, 1, 0.5, 0) \\ g = AB^T=\left( \begin{array}{ccccc} 0 & 0 & 0 & 0 & 0 \\ 0 & 0.25 & 0.5 & 0.25 & 0 \\ 0 & 0.5 & 1 & 0.5 & 0 \\ 0 & 0.25 & 0.5 & 0.25 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} \right) \]