摄像机
在本部分中,
- 将介绍多视角几何的基础知识
- 将了解极点、极线、极约束等内容。
基本概念
使用针孔相机拍摄图像时,我们将丢失一个重要信息,即图像的深度。或者,图像中每个点距离相机的距离由于这是 3D 到 2D 的转换。因此,一个重要的未知数是,我们是否可以使用这些相机找到深度信息。答案即是使用多于一台相机。我们的眼睛以类似的方式工作,使用两台相机(两只眼睛),这被称为立体视觉。所以让我们了解 OpenCV 在此领域提供了什么。
(Gary Bradsky 的《OpenCV 教程》在该领域有很多信息。)
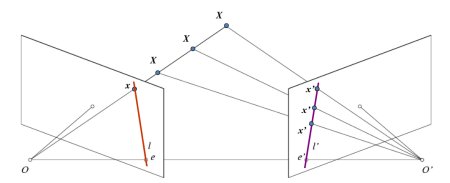
在讨论深度图像之前,让我们首先了解多视角几何中的一些基本概念。在本部分中,我们将讨论极线几何。请参见下图,其中显示了两个相机拍摄同一场景图像的基本设置。
图像
如果我们只使用左侧相机,将无法找到图像中点 \(x\) 对应的 3D 点,因为 \(OX\) 线上的每个点都投影到图像平面上的同一个点。但同时考虑右侧图像。现在,\(OX\) 线上的不同点投影到右侧平面的不同点(\(x'\))。因此,通过这两幅图像,我们可以三角化正确 3D 点。这就是这个想法。
不同点在 \(OX\) 上的投影在右侧平面(线段 \(l'\))上形成一条线。我们称之为点 \(x\) 对应的极线。这意味着,要找到右侧图像上的点 \(x\),需沿着极线搜索。它应位于这条线上的某个位置(可以这样思考,要找到另一幅图像中的匹配点,不需要搜索整个图像,只需沿着极线搜索即可。这样可以提供更好的性能和准确性)。这称为极线约束。类似地,所有点都会在另一幅图像中与其对应的极线。平面 \(XOO'\) 称为极平面。
\(O\) 和 \(O'\) 为相机中心点。从上面的设置中,你可以看到右相机 \(O'\) 的投影在左图像中的点 \(e\) 处可见。它被称为**极点**。极点为过相机中心和图像平面的线段的交点。类似地,\(e'\) 为左相机的极点。在一些情况下,你无法在图像中找到极点,它们可能在图像外部(这意味着一个相机看不到另一个相机)。
所有极线都通过其极点。因此,为了找到极点的位置,我们可以找到很多极线并找出它们的交点。
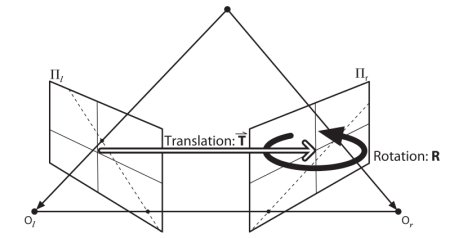
因此在本节中,我们专注于寻找极线和极点。但要找到它们,我们需要另外两种元素:**基础矩阵 (F)** 和**本质矩阵 (E)**。本质矩阵包含关于平移和旋转的信息,描述了第二个相机相对于全局坐标系中的第一个相机的相对于位置。参见下图(图片由 Gary Bradsky 惠赠,出自《Learning OpenCV》)
图像
但是,我们更喜欢使用像素坐标进行测量,对吗?基础矩阵中包含与本质矩阵相同的信息,此外还包含有关两台相机的内参信息,这样我们就可以在像素坐标中关联两台相机。(如果我们使用校正图像并通过焦距进行点归一化,\(F=E\)。简单来说,基础矩阵 F 将一个图像中的点映射到另一图像中的一条线(极线)。这个矩阵是通过匹配两幅图像中的点计算得出的。至少需要 8 个此类点才能找到基础矩阵(使用 8 点算法时)。建议使用更多点并使用 RANSAC 来获得更鲁棒的结果。
代码
因此,首先我们需要在两幅图像间找到尽可能多的匹配项,以找到基础矩阵。为此,我们使用基于 FLANN 的匹配器和比率测试的 SIFT 描述符。
import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt
img1 =
cv.imread(
'myleft.jpg', cv.IMREAD_GRAYSCALE)
img2 =
cv.imread(
'myright.jpg', cv.IMREAD_GRAYSCALE)
sift = cv.SIFT_create()
kp1, des1 = sift.detectAndCompute(img1,None)
kp2, des2 = sift.detectAndCompute(img2,None)
FLANN_INDEX_KDTREE = 1
index_params = dict(algorithm = FLANN_INDEX_KDTREE, trees = 5)
search_params = dict(checks=50)
matches = flann.knnMatch(des1, des2, k=2)
pts1 = []
pts2 = []
for i, (m, n) in enumerate(matches)
if m.distance < 0.8*n.distance
pts2.append(kp2[m.trainIdx].pt)
pts1.append(kp1[m.queryIdx].pt)
基于 Flann 的描述符匹配器。
定义 features2d.hpp:1294
CV_EXPORTS_W Mat imread(const String &filename, int flags=IMREAD_COLOR)
从文件中加载图像。
现在,我们已经有了两幅图像中最佳匹配的列表。让我们找到基本矩阵。
pts1 = np.int32(pts1)
pts2 = np.int32(pts2)
pts1 = pts1[mask.ravel()==1]
pts2 = pts2[mask.ravel()==1]
Mat findFundamentalMat(InputArray points1, InputArray points2, int method, double ransacReprojThreshold, double confidence, int maxIters, OutputArray mask=noArray())
根据两幅图像中的对应点计算基本矩阵。
接下来,我们找到极线。绘制第一幅图像中极线与第二幅图像中的点相对应的情况。因此,这里正确提及图像很重要。我们获得了一个线条数组。因此,我们定义了一个新函数在图像上绘制这些线条。
def drawlines(img1, img2, lines, pts1, pts2)
''' img1 - 我们针对 img2 中的点绘制极线的图像
lines - 对应的极线 '''
r, c = img1.shape
for r, pt1, pt2 in zip(lines, pts1, pts2)
color = tuple(np.random.randint(0, 255, 3).tolist())
x0, y0 = map(int, [0, -r[2]/r[1] ])
x1, y1 = map(int, [c, -(r[2]+r[0]*c)/r[1] ])
img1 =
cv.line(img1, (x0, y0), (x1, y1), color, 1)
img1 =
cv.circle(img1, tuple(pt1), 5, color, -1)
img2 =
cv.circle(img2, tuple(pt2), 5, color, -1)
return img1, img2
void cvtColor(InputArray src, OutputArray dst, int code, int dstCn=0)
将图像从一种颜色空间转换为另一种颜色空间。
void line(InputOutputArray img, Point pt1, Point pt2, const Scalar &color, int thickness=1, int lineType=LINE_8, int shift=0)
绘制连接两个点的线段。
void circle(InputOutputArray img, Point center, int radius, const Scalar &color, int thickness=1, int lineType=LINE_8, int shift=0)
绘制圆形。
现在我们在两幅图像中找到极线并绘制它们。
lines1 = lines1.reshape(-1,3)
img5,img6 = drawlines(img1,img2,lines1,pts1,pts2)
lines2 = lines2.reshape(-1,3)
img3,img4 = drawlines(img2,img1,lines2,pts2,pts1)
plt.subplot(121),plt.imshow(img5)
plt.subplot(122),plt.imshow(img3)
plt.show()
void computeCorrespondEpilines(InputArray points, int whichImage, InputArray F, OutputArray lines)
对于立体对图像中的点,计算另一幅图像中的对应极线。
下面是我们得到的结果

图像
您可以在左图像中看到,所有极线都在图像右侧的一个点之外会聚。那个会聚点即极点。
为了得到更好的结果,应该使用具有良好分辨率和大量非平面点的图像。
附加资源
练习
- 一个重要的话题是摄像机的向前移动。然后极点将在两个极点中看到相同的位置,并且极线将从一个固定点出现。 参见此讨论。
- 基础矩阵估计对匹配质量、离群点等很敏感。当所有选取的匹配点都位于同一平面上时,情况会变得更糟。 查看此讨论。





 1.9.8 生成
1.9.8 生成