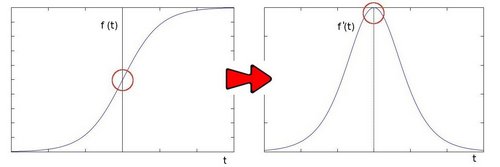
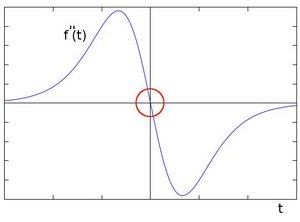
import org.opencv.core.*;
import org.opencv.highgui.HighGui;
import org.opencv.imgcodecs.Imgcodecs;
import org.opencv.imgproc.Imgproc;
class LaplaceDemoRun {
public void run(String[] args) {
Mat src, src_gray = new Mat(), dst = new Mat();
int kernel_size = 3;
int scale = 1;
int delta = 0;
int ddepth = CvType.CV_16S;
String window_name = "Laplace Demo";
String imageName = ((args.length > 0) ? args[0] : "../data/lena.jpg");
src = Imgcodecs.imread(imageName, Imgcodecs.IMREAD_COLOR);
if( src.empty() ) {
System.out.println("Error opening image");
System.out.println("Program Arguments: [image_name -- default ../data/lena.jpg] \n");
System.exit(-1);
}
Imgproc.GaussianBlur( src, src, new Size(3, 3), 0, 0, Core.BORDER_DEFAULT );
Imgproc.cvtColor( src, src_gray, Imgproc.COLOR_RGB2GRAY );
Mat abs_dst = new Mat();
Imgproc.Laplacian( src_gray, dst, ddepth, kernel_size, scale, delta, Core.BORDER_DEFAULT );
Core.convertScaleAbs( dst, abs_dst );
HighGui.imshow( window_name, abs_dst );
HighGui.waitKey(0);
System.exit(0);
}
}
public class LaplaceDemo {
public static void main(String[] args) {
System.loadLibrary(Core.NATIVE_LIBRARY_NAME);
new LaplaceDemoRun().run(args);
}
}