上一教程： 轮廓：入门
下一教程： 轮廓属性

目标

查找轮廓的不同特征，例如面积、周长、质心、边界框等。
您将学习许多与轮廓相关的函数。

1. 矩

图像矩帮助您计算一些特征，例如物体的质心、物体的面积等。查看维基百科页面上的图像矩

我们使用函数：cv.moments (array, binaryImage = false)

参数

array	栅格图像（单通道、8 位或浮点型二维数组）或二维点的数组（1×N 或 N×1）。
binaryImage	如果为真，则所有非零图像像素都视为 1。此参数仅用于图像。

试试看

从这些矩中，您可以提取有用的数据，例如面积、质心等。质心由关系式给出，\(C_x = \frac{M_{10}}{M_{00}}\) 和 \(C_y = \frac{M_{01}}{M_{00}}\)。这可以按如下方式完成

let cx = M.m10/M.m00

let cy = M.m01/M.m00

2. 轮廓面积

轮廓面积由函数cv.contourArea() 或从矩M['m00']给出。

我们使用函数：cv.contourArea (contour, oriented = false)

参数

contour	输入二维点向量（轮廓顶点）
oriented	定向面积标志。如果为真，则函数返回有符号的面积值，具体取决于轮廓方向（顺时针或逆时针）。使用此功能，您可以通过取面积的符号来确定轮廓的方向。默认情况下，参数为 false，这意味着返回绝对值。

试试看

3. 轮廓周长

也称为弧长。可以使用cv.arcLength()函数计算出来。

我们使用函数：cv.arcLength (curve, closed)

参数

curve	输入二维点向量。
closed	指示曲线是否闭合的标志。

试试看

4. 轮廓逼近

它根据我们指定的精度将轮廓形状逼近到具有较少顶点的另一种形状。它是道格拉斯-普克算法的实现。查看维基百科页面以了解算法和演示。

我们使用函数：cv.approxPolyDP (curve, approxCurve, epsilon, closed)

参数

curve	存储在cv.Mat中的输入二维点向量。
approxCurve	逼近的结果。类型应与输入曲线的类型匹配。
epsilon	指定逼近精度的参数。这是原始曲线与其逼近之间最大距离。
closed	如果为真，则逼近曲线是闭合的（其第一个和最后一个顶点相连）。否则，它不是闭合的。

试试看

5. 凸包

凸包看起来类似于轮廓逼近，但它不是（在某些情况下两者可能提供相同的结果）。在这里，cv.convexHull()函数检查曲线的凸性缺陷并对其进行校正。一般来说，凸曲线是指始终向外凸出或至少平坦的曲线。如果向内凸出，则称为凸性缺陷。例如，检查下面的手部图像。红线显示手的凸包。双向箭头标记显示凸性缺陷，它们是凸包与轮廓的局部最大偏差。

图像

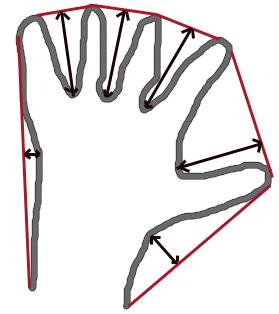
我们使用函数：cv.convexHull (points, hull, clockwise = false, returnPoints = true)

参数

points	输入二维点集。
hull	输出凸包。
clockwise	方向标志。如果为真，则输出凸包按顺时针方向定向。否则，它按逆时针方向定向。假定的坐标系其 X 轴指向右侧，其 Y 轴指向向上。
returnPoints	操作标志。对于矩阵，当标志为真时，函数返回凸包点。否则，它返回凸包点的索引。

试试看

6. 检查凸性

有一个函数可以检查曲线是否为凸的，cv.isContourConvex()。它只返回真或假。没什么大不了的。

cv.isContourConvex(cnt);

7. 边界矩形

有两种类型的边界矩形。

7.a. 正向边界矩形

这是一个正向矩形，它不考虑物体的旋转。因此，边界矩形的面积不会最小。

我们使用函数：cv.boundingRect (points)

参数

points 输入二维点集。

试试看

7.b. 旋转矩形

在这里，边界矩形以最小面积绘制，因此它也考虑了旋转。

我们使用函数：cv.minAreaRect (points)

参数

points 输入二维点集。

试一试

8. 最小外接圆

接下来，我们使用函数cv.minEnclosingCircle()查找对象的圆周。这是一个完全覆盖具有最小面积的对象的圆。

我们使用以下函数：cv.minEnclosingCircle (points)

参数

points 输入二维点集。

cv.circle (img, center, radius, color, thickness = 1, lineType = cv.LINE_8, shift = 0)

参数

img	绘制圆形的图像。
center	圆心。
radius	圆的半径。
color	圆的颜色。
thickness	圆轮廓的厚度，如果为正数。负厚度表示要绘制填充的圆。
lineType	圆边界的类型。
shift	中心坐标和半径值中的分数位数。

试一试

9. 拟合椭圆

下一个是将椭圆拟合到对象。它返回内接椭圆的旋转矩形。我们使用以下函数：cv.fitEllipse (points)

参数

points 输入二维点集。

cv.ellipse1 (img, box, color, thickness = 1, lineType = cv.LINE_8)

参数

img	图像。
box	通过 RotatedRect 表示的替代椭圆。这意味着该函数绘制内接于旋转矩形的椭圆。
color	椭圆颜色。
thickness	椭圆弧轮廓的厚度，如果为正数。否则，这表示要绘制填充的椭圆扇区。
lineType	椭圆边界的类型。

试一试

10. 拟合直线

类似地，我们可以将一条线拟合到一组点上。我们可以将一条直线近似到它。

我们使用以下函数：cv.fitLine (points, line, distType, param, reps, aeps)

参数

points	输入二维点集。
line	输出线参数。它应该是一个包含 4 个元素 [vx, vy, x0, y0] 的 Mat，其中 [vx, vy] 是与线共线的归一化向量，[x0, y0] 是线上的一个点。
distType	M 估计量使用的距离（参见 cv.DistanceTypes）。
param	某些类型距离的数值参数 (C)。如果为 0，则选择最佳值。
reps	半径（坐标原点与直线之间的距离）的足够精度。
aeps	角度的足够精度。对于 reps 和 aeps，0.01 将是一个很好的默认值。

cv.line (img, pt1, pt2, color, thickness = 1, lineType = cv.LINE_8, shift = 0)

参数

img	图像。
pt1	线段的第一个点。
pt2	线段的第二个点。
color	线条颜色。
thickness	线宽。
lineType	线的类型。
shift	点坐标中的分数位数。