主成分分析 (PCA) 简介

目录

• 目标
• 什么是 PCA？
• 特征向量和特征值是如何计算的？
• 源代码
• 解释
• 结果

上一篇教程： 非线性可分数据的支持向量机

原始作者	Theodore Tsesmelis
兼容性	OpenCV >= 3.0

目标

在本教程中，您将学习如何

• 使用 OpenCV 类 cv::PCA 来计算对象的方向。

什么是 PCA？

主成分分析 (PCA) 是一种统计方法，用于提取数据集中最重要的特征。

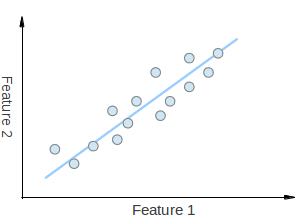
考虑图中的一组二维点。每个维度对应一个您感兴趣的特征。有人可能会争辩说这些点是随机排列的。然而，如果您仔细观察，会发现存在一个难以忽视的线性模式（由蓝线指示）。PCA 的一个关键点是降维。降维是减少给定数据集维度数量的过程。例如，在上述情况下，可以将点集近似为一条直线，从而将给定点的维度从二维降到一维。

此外，您还可以看到这些点沿蓝线的变化最大，比沿特征 1 轴或特征 2 轴的变化更大。这意味着如果您知道点沿蓝线的位置，您将比只知道点在特征 1 轴或特征 2 轴上的位置拥有更多的信息。

因此，PCA 允许我们找到数据变化最大的方向。实际上，对图中点集运行 PCA 的结果是两个向量，称为特征向量，它们是数据集的主成分。

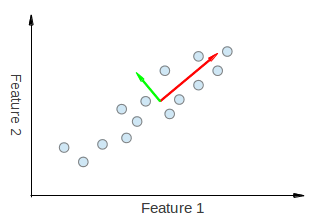
每个特征向量的大小编码在相应的特征值中，并指示数据沿主成分变化的程度。特征向量的起点是数据集中所有点的中心。将 PCA 应用于 N 维数据集会得到 N 个 N 维特征向量、N 个特征值和 1 个 N 维中心点。理论够了，让我们看看如何将这些思想付诸代码。

特征向量和特征值是如何计算的？

目标是将给定维度为 p 的数据集 X 转换为维度更小 L 的替代数据集 Y。等效地，我们正在寻找矩阵 Y，其中 Y 是矩阵 X 的 Karhunen–Loève 变换 (KLT)

\[ \mathbf{Y} = \mathbb{K} \mathbb{L} \mathbb{T} \{\mathbf{X}\} \]

组织数据集

假设您有一个包含 p 个变量观测值的数据集，并且您希望减少数据，使得每个观测值仅用 L 个变量描述，其中 L < p。进一步假设数据排列为一组 n 个数据向量 \( x_1...x_n \)，其中每个 \( x_i \) 代表 p 个变量的单个分组观测值。

• 将 \( x_1...x_n \) 写为行向量，每个行向量有 p 列。
• 将这些行向量放入一个维度为 \( n\times p \) 的单个矩阵 X 中。

计算经验均值

• 沿着每个维度 \( j = 1, ..., p \) 找到经验均值。

• 将计算出的均值放入一个维度为 \( p\times 1 \) 的经验均值向量 u 中。

  \[ \mathbf{u[j]} = \frac{1}{n}\sum_{i=1}^{n}\mathbf{X[i,j]} \]

计算与均值的偏差

均值减法是寻找使数据近似的均方误差最小化的主成分基的解决方案中不可或缺的一部分。因此，我们通过以下方式对数据进行中心化处理：

• 从数据矩阵 X 的每一行中减去经验均值向量 u。

• 将减去均值后的数据存储在 \( n\times p \) 矩阵 B 中。

  \[ \mathbf{B} = \mathbf{X} - \mathbf{h}\mathbf{u^{T}} \]

  其中 h 是一个所有元素为 1 的 \( n\times 1 \) 列向量

  \[ h[i] = 1, i = 1, ..., n \]

找到协方差矩阵

• 通过矩阵 B 与自身的外积找到 \( p\times p \) 经验协方差矩阵 C

  \[ \mathbf{C} = \frac{1}{n-1} \mathbf{B^{*}} \cdot \mathbf{B} \]

  其中 * 是共轭转置运算符。请注意，如果 B 完全由实数组成（许多应用中都是如此），则“共轭转置”与常规转置相同。

找到协方差矩阵的特征向量和特征值

• 计算使协方差矩阵 C 对角化的特征向量矩阵 V

  \[ \mathbf{V^{-1}} \mathbf{C} \mathbf{V} = \mathbf{D} \]

  其中 D 是 C 的特征值的对角矩阵。

• 矩阵 D 将采用 \( p \times p \) 对角矩阵的形式

  \[ D[k,l] = \left\{\begin{matrix} \lambda_k, k = l \\ 0, k \neq l \end{matrix}\right. \]

  这里，\( \lambda_j \) 是协方差矩阵 C 的第 j 个特征值

• 矩阵 V 的维度也是 p x p，包含 p 个列向量，每个向量的长度为 p，它们代表协方差矩阵 C 的 p 个特征向量。
• 特征值和特征向量是成对且有序的。第 j 个特征值对应于第 j 个特征向量。

注意

来源 [1], [2]，并特别感谢 Svetlin Penkov 的原创教程。

源代码

C++

• 可下载代码：点击此处
• 代码速览

   
  #include "opencv2/core.hpp"
  #include "opencv2/imgproc.hpp"
  #include "opencv2/highgui.hpp"
  #include <iostream>
   
  using namespace std;
  using namespace cv;
   
  // 函数声明
  void drawAxis(Mat&, Point, Point, Scalar, const float);
  double getOrientation(const vector<Point> &, Mat&);
   
  void drawAxis(Mat& img, Point p, Point q, Scalar colour, const float scale = 0.2)
  {
      double angle = atan2( (double) p.y - q.y, (double) p.x - q.x ); // 角度（弧度）
      double hypotenuse = sqrt( (double) (p.y - q.y) * (p.y - q.y) + (p.x - q.x) * (p.x - q.x));
   
      // 这里我们将箭头长度缩放 scale 倍
  q.x = (int) (p.x - scale * hypotenuse * cos(angle));
  q.y = (int) (p.y - scale * hypotenuse * sin(angle));
  line(img, p, q, colour, 1, LINE_AA);
   
      // 创建箭头钩
  p.x = (int) (q.x + 9 * cos(angle + CV_PI / 4));
  p.y = (int) (q.y + 9 * sin(angle + CV_PI / 4));
  line(img, p, q, colour, 1, LINE_AA);
   
  p.x = (int) (q.x + 9 * cos(angle - CV_PI / 4));
  p.y = (int) (q.y + 9 * sin(angle - CV_PI / 4));
  line(img, p, q, colour, 1, LINE_AA);
  }
   
  double getOrientation(const vector<Point> &pts, Mat &img)
  {
      // 构建 PCA 分析使用的缓冲区
      int sz = static_cast<int>(pts.size());
      Mat data_pts = Mat(sz, 2, CV_64F);
      for (int i = 0; i < data_pts.rows; i++)
      {
  data_pts.at<double>(i, 0) = pts[i].x;
  data_pts.at<double>(i, 1) = pts[i].y;
      }
   
      // 执行 PCA 分析
      PCA pca_analysis(data_pts, Mat(), PCA::DATA_AS_ROW);
   
      // 存储对象的中心
      Point cntr = Point(static_cast<int>(pca_analysis.mean.at<double>(0, 0)),
                        static_cast<int>(pca_analysis.mean.at<double>(0, 1)));
   
      // 存储特征值和特征向量
  vector<Point2d> eigen_vecs(2);
  vector<double> eigen_val(2);
      for (int i = 0; i < 2; i++)
      {
  eigen_vecs[i] = Point2d(pca_analysis.eigenvectors.at<double>(i, 0),
  pca_analysis.eigenvectors.at<double>(i, 1));
   
  eigen_val[i] = pca_analysis.eigenvalues.at<double>(i);
      }
   
      // 绘制主成分
  circle(img, cntr, 3, Scalar(255, 0, 255), 2);
      Point p1 = cntr + 0.02 * Point(static_cast<int>(eigen_vecs[0].x * eigen_val[0]), static_cast<int>(eigen_vecs[0].y * eigen_val[0]));
      Point p2 = cntr - 0.02 * Point(static_cast<int>(eigen_vecs[1].x * eigen_val[1]), static_cast<int>(eigen_vecs[1].y * eigen_val[1]));
  drawAxis(img, cntr, p1, Scalar(0, 255, 0), 1);
  drawAxis(img, cntr, p2, Scalar(255, 255, 0), 5);
   
      double angle = atan2(eigen_vecs[0].y, eigen_vecs[0].x); // 方向（弧度）
   
      return angle;
  }
   
  int main(int argc, char** argv)
  {
      // 加载图像
      CommandLineParser parser(argc, argv, "{@input | pca_test1.jpg | input image}");
  parser.about( "此程序演示了如何使用 OpenCV PCA 提取对象的方向。\n" );
  parser.printMessage();
   
      Mat src = imread( samples::findFile( parser.get<String>("@input") ) );
   
      // 检查图像是否成功加载
      if(src.empty())
      {
  cout << "Problem loading image!!!" << endl;
          return EXIT_FAILURE;
      }
   
      imshow("src", src);
   
      // 将图像转换为灰度图像
      Mat gray;
      cvtColor(src, gray, COLOR_BGR2GRAY);
   
      // 将图像转换为二值图像
      Mat bw;
      threshold(gray, bw, 50, 255, THRESH_BINARY | THRESH_OTSU);
   
      // 查找阈值图像中的所有轮廓
  vector<vector<Point> > contours;
      findContours(bw, contours, RETR_LIST, CHAIN_APPROX_NONE);
   
      for (size_t i = 0; i < contours.size(); i++)
      {
          // 计算每个轮廓的面积
          double area = contourArea(contours[i]);
          // 忽略太小或太大的轮廓
          if (area < 1e2 || 1e5 < area) continue;
   
          // 仅为了可视化目的绘制每个轮廓
          drawContours(src, contours, static_cast<int>(i), Scalar(0, 0, 255), 2);
          // 查找每个形状的方向
  getOrientation(contours[i], src);
      }
   
      imshow("output", src);
   
      waitKey();
      return EXIT_SUCCESS;
  }

Java

• 可下载代码：点击此处
• 代码速览

  import java.util.ArrayList;
  import java.util.List;
   
  import org.opencv.core.Core;
  import org.opencv.core.CvType;
  import org.opencv.core.Mat;
  import org.opencv.core.MatOfPoint;
  import org.opencv.core.Point;
  import org.opencv.core.Scalar;
  import org.opencv.highgui.HighGui;
  import org.opencv.imgcodecs.Imgcodecs;
  import org.opencv.imgproc.Imgproc;
   
  //此程序演示了如何使用 OpenCV PCA 提取对象的方向。
  class IntroductionToPCA {
      private void drawAxis(Mat img, Point p_, Point q_, Scalar colour, float scale) {
  Point p = new Point(p_.x, p_.y);
  Point q = new Point(q_.x, q_.y);
          double angle = Math.atan2(p.y - q.y, p.x - q.x); // 角度（弧度）
          double hypotenuse = Math.sqrt((p.y - q.y) * (p.y - q.y) + (p.x - q.x) * (p.x - q.x));
   
          // 这里我们将箭头长度缩放 scale 倍
  q.x = (int) (p.x - scale * hypotenuse * Math.cos(angle));
  q.y = (int) (p.y - scale * hypotenuse * Math.sin(angle));
  Imgproc.line(img, p, q, colour, 1, Imgproc.LINE_AA, 0);
   
          // 创建箭头钩
  p.x = (int) (q.x + 9 * Math.cos(angle + Math.PI / 4));
  p.y = (int) (q.y + 9 * Math.sin(angle + Math.PI / 4));
  Imgproc.line(img, p, q, colour, 1, Imgproc.LINE_AA, 0);
   
  p.x = (int) (q.x + 9 * Math.cos(angle - Math.PI / 4));
  p.y = (int) (q.y + 9 * Math.sin(angle - Math.PI / 4));
  Imgproc.line(img, p, q, colour, 1, Imgproc.LINE_AA, 0);
      }
   
      private double getOrientation(MatOfPoint ptsMat, Mat img) {
  List<Point> pts = ptsMat.toList();
          // Construct a buffer used by the pca analysis
          int sz = pts.size();
  Mat dataPts = new Mat(sz, 2, CvType.CV_64F);
          double[] dataPtsData = new double[(int) (dataPts.total() * dataPts.channels())];
          for (int i = 0; i < dataPts.rows(); i++) {
  dataPtsData[i * dataPts.cols()] = pts.get(i).x;
  dataPtsData[i * dataPts.cols() + 1] = pts.get(i).y;
          }
  dataPts.put(0, 0, dataPtsData);
   
          // 执行 PCA 分析
  Mat mean = new Mat();
  Mat eigenvectors = new Mat();
  Mat eigenvalues = new Mat();
  Core.PCACompute2(dataPts, mean, eigenvectors, eigenvalues);
          double[] meanData = new double[(int) (mean.total() * mean.channels())];
  mean.get(0, 0, meanData);
   
          // Store the center of the object
  Point cntr = new Point(meanData[0], meanData[1]);
   
          // Store the eigenvalues and eigenvectors
          double[] eigenvectorsData = new double[(int) (eigenvectors.total() * eigenvectors.channels())];
          double[] eigenvaluesData = new double[(int) (eigenvalues.total() * eigenvalues.channels())];
  eigenvectors.get(0, 0, eigenvectorsData);
  eigenvalues.get(0, 0, eigenvaluesData);
   
          // 绘制主成分
  Imgproc.circle(img, cntr, 3, new Scalar(255, 0, 255), 2);
  Point p1 = new Point(cntr.x + 0.02 * eigenvectorsData[0] * eigenvaluesData[0],
  cntr.y + 0.02 * eigenvectorsData[1] * eigenvaluesData[0]);
  Point p2 = new Point(cntr.x - 0.02 * eigenvectorsData[2] * eigenvaluesData[1],
  cntr.y - 0.02 * eigenvectorsData[3] * eigenvaluesData[1]);
  drawAxis(img, cntr, p1, new Scalar(0, 255, 0), 1);
  drawAxis(img, cntr, p2, new Scalar(255, 255, 0), 5);
   
          double angle = Math.atan2(eigenvectorsData[1], eigenvectorsData[0]); // 方向（弧度）
   
          return angle;
      }
   
      public void run(String[] args) {
          // 加载图像
  String filename = args.length > 0 ? args[0] : "../data/pca_test1.jpg";
  Mat src = Imgcodecs.imread(filename);
   
          // 检查图像是否成功加载
          if (src.empty()) {
  System.err.println("无法读取图像: " + filename);
  System.exit(0);
          }
   
  Mat srcOriginal = src.clone();
  HighGui.imshow("src", srcOriginal);
   
          // 将图像转换为灰度图像
  Mat gray = new Mat();
  Imgproc.cvtColor(src, gray, Imgproc.COLOR_BGR2GRAY);
   
          // 将图像转换为二值图像
  Mat bw = new Mat();
  Imgproc.threshold(gray, bw, 50, 255, Imgproc.THRESH_BINARY | Imgproc.THRESH_OTSU);
   
          // 查找阈值图像中的所有轮廓
  List<MatOfPoint> contours = new ArrayList<>();
  Mat hierarchy = new Mat();
  Imgproc.findContours(bw, contours, hierarchy, Imgproc.RETR_LIST, Imgproc.CHAIN_APPROX_NONE);
   
          for (int i = 0; i < contours.size(); i++) {
              // 计算每个轮廓的面积
              double area = Imgproc.contourArea(contours.get(i));
              // 忽略太小或太大的轮廓
              if (area < 1e2 || 1e5 < area)
                  continue;
   
              // 仅为了可视化目的绘制每个轮廓
  Imgproc.drawContours(src, contours, i, new Scalar(0, 0, 255), 2);
              // 查找每个形状的方向
  getOrientation(contours.get(i), src);
          }
   
  HighGui.imshow("output", src);
   
  HighGui.waitKey();
  System.exit(0);
      }
  }
   
  public class IntroductionToPCADemo {
      public static void main(String[] args) {
          // 加载本地 OpenCV 库
  System.loadLibrary(Core.NATIVE_LIBRARY_NAME);
   
          new IntroductionToPCA().run(args);
      }
  }

Python

• 可下载代码：点击此处
• 代码速览

  from __future__ import print_function
  from __future__ import division
  import cv2 as cv
  import numpy as np
  import argparse
  from math import atan2, cos, sin, sqrt, pi
   
  def drawAxis(img, p_, q_, colour, scale)
  p = list(p_)
  q = list(q_)
      
  angle = atan2(p[1] - q[1], p[0] - q[0]) # 角度（弧度）
  hypotenuse = sqrt((p[1] - q[1]) * (p[1] - q[1]) + (p[0] - q[0]) * (p[0] - q[0]))
   
      # 在此处我们将箭头按比例因子加长
  q[0] = p[0] - scale * hypotenuse * cos(angle)
  q[1] = p[1] - scale * hypotenuse * sin(angle)
      cv.line(img, (int(p[0]), int(p[1])), (int(q[0]), int(q[1])), colour, 1, cv.LINE_AA)
   
      # 创建箭头倒钩
  p[0] = q[0] + 9 * cos(angle + pi / 4)
  p[1] = q[1] + 9 * sin(angle + pi / 4)
      cv.line(img, (int(p[0]), int(p[1])), (int(q[0]), int(q[1])), colour, 1, cv.LINE_AA)
   
  p[0] = q[0] + 9 * cos(angle - pi / 4)
  p[1] = q[1] + 9 * sin(angle - pi / 4)
      cv.line(img, (int(p[0]), int(p[1])), (int(q[0]), int(q[1])), colour, 1, cv.LINE_AA)
      
   
  def getOrientation(pts, img)
      
  sz = len(pts)
  data_pts = np.empty((sz, 2), dtype=np.float64)
      for i in range(data_pts.shape[0])
  data_pts[i,0] = pts[i,0,0]
  data_pts[i,1] = pts[i,0,1]
   
      # 执行 PCA 分析
  mean = np.empty((0))
  mean, eigenvectors, eigenvalues = cv.PCACompute2(data_pts, mean)
   
      # Store the center of the object
  cntr = (int(mean[0,0]), int(mean[0,1]))
      
   
      
      cv.circle(img, cntr, 3, (255, 0, 255), 2)
  p1 = (cntr[0] + 0.02 * eigenvectors[0,0] * eigenvalues[0,0], cntr[1] + 0.02 * eigenvectors[0,1] * eigenvalues[0,0])
  p2 = (cntr[0] - 0.02 * eigenvectors[1,0] * eigenvalues[1,0], cntr[1] - 0.02 * eigenvectors[1,1] * eigenvalues[1,0])
  drawAxis(img, cntr, p1, (0, 255, 0), 1)
  drawAxis(img, cntr, p2, (255, 255, 0), 5)
   
  angle = atan2(eigenvectors[0,1], eigenvectors[0,0]) # 方向（弧度）
      
   
      return angle
   
   
  parser = argparse.ArgumentParser(description='主成分分析 (PCA) 教程代码。\
  本程序演示如何使用 OpenCV PCA 提取对象的方向。')
  parser.add_argument('--input', help='输入图像的路径。', default='pca_test1.jpg')
  args = parser.parse_args()
   
  src = cv.imread(cv.samples.findFile(args.input))
  # 检查图像是否成功加载
  if src is None
  print('无法打开或找到图像：', args.input)
  exit(0)
   
  cv.imshow('src', src)
   
  # 将图像转换为灰度图
  gray = cv.cvtColor(src, cv.COLOR_BGR2GRAY)
   
  # 将图像转换为二值图
  _, bw = cv.threshold(gray, 50, 255, cv.THRESH_BINARY | cv.THRESH_OTSU)
   
   
   
  contours, _ = cv.findContours(bw, cv.RETR_LIST, cv.CHAIN_APPROX_NONE)
   
  for i, c in enumerate(contours)
      # 计算每个轮廓的面积
  area = cv.contourArea(c)
      # 忽略过小或过大的轮廓
      if area < 1e2 or 1e5 < area
          continue
   
      # 仅为可视化目的绘制每个轮廓
      cv.drawContours(src, contours, i, (0, 0, 255), 2)
      # 查找每个形状的方向
  getOrientation(c, src)
   
   
  cv.imshow('output', src)
  cv.waitKey()

注意

另一个使用 PCA 进行降维并保持一定方差的示例可以在 opencv_source_code/samples/cpp/pca.cpp 找到。

解释

• 读取图像并将其转换为二值图

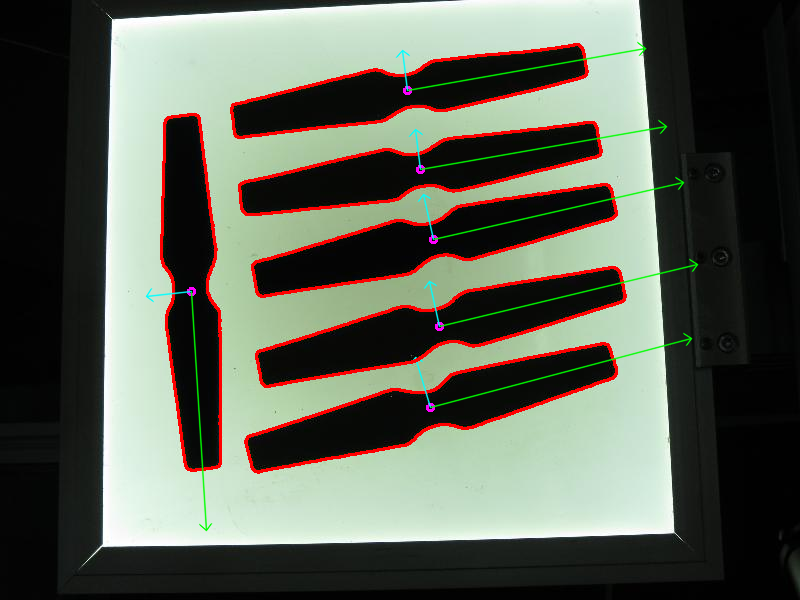
在这里，我们应用必要的预处理程序，以便能够检测感兴趣的对象。

C++

    // 加载图像
    CommandLineParser parser(argc, argv, "{@input | pca_test1.jpg | input image}");
parser.about( "此程序演示了如何使用 OpenCV PCA 提取对象的方向。\n" );
parser.printMessage();
 
    Mat src = imread( samples::findFile( parser.get<String>("@input") ) );
 
    // 检查图像是否成功加载
    if(src.empty())
    {
cout << "Problem loading image!!!" << endl;
        return EXIT_FAILURE;
    }
 
    imshow("src", src);
 
    // 将图像转换为灰度图像
    Mat gray;
    cvtColor(src, gray, COLOR_BGR2GRAY);
 
    // 将图像转换为二值图像
    Mat bw;
    threshold(gray, bw, 50, 255, THRESH_BINARY | THRESH_OTSU);

Java

        // 加载图像
        String filename = args.length > 0 ? args[0] : "../data/pca_test1.jpg";
Mat src = Imgcodecs.imread(filename);
 
        // 检查图像是否成功加载
        if (src.empty()) {
System.err.println("无法读取图像: " + filename);
System.exit(0);
        }
 
Mat srcOriginal = src.clone();
HighGui.imshow("src", srcOriginal);
 
        // 将图像转换为灰度图像
Mat gray = new Mat();
Imgproc.cvtColor(src, gray, Imgproc.COLOR_BGR2GRAY);
 
        // 将图像转换为二值图像
Mat bw = new Mat();
Imgproc.threshold(gray, bw, 50, 255, Imgproc.THRESH_BINARY | Imgproc.THRESH_OTSU);

Python

parser = argparse.ArgumentParser(description='主成分分析 (PCA) 教程代码。\
本程序演示如何使用 OpenCV PCA 提取对象的方向。')
parser.add_argument('--input', help='输入图像的路径。', default='pca_test1.jpg')
args = parser.parse_args()
 
src = cv.imread(cv.samples.findFile(args.input))
# 检查图像是否成功加载
if src is None
print('无法打开或找到图像：', args.input)
exit(0)
 
cv.imshow('src', src)
 
# 将图像转换为灰度图
gray = cv.cvtColor(src, cv.COLOR_BGR2GRAY)
 
# 将图像转换为二值图
_, bw = cv.threshold(gray, 50, 255, cv.THRESH_BINARY | cv.THRESH_OTSU)

• 提取感兴趣的对象

然后通过大小查找和过滤轮廓，并获取剩余轮廓的方向。

C++

    // 查找阈值图像中的所有轮廓
vector<vector<Point> > contours;
    findContours(bw, contours, RETR_LIST, CHAIN_APPROX_NONE);
 
    for (size_t i = 0; i < contours.size(); i++)
    {
        // 计算每个轮廓的面积
        double area = contourArea(contours[i]);
        // 忽略太小或太大的轮廓
        if (area < 1e2 || 1e5 < area) continue;
 
        // 仅为了可视化目的绘制每个轮廓
        drawContours(src, contours, static_cast<int>(i), Scalar(0, 0, 255), 2);
        // 查找每个形状的方向
getOrientation(contours[i], src);
    }

Java

        // 查找阈值图像中的所有轮廓
List<MatOfPoint> contours = new ArrayList<>();
Mat hierarchy = new Mat();
Imgproc.findContours(bw, contours, hierarchy, Imgproc.RETR_LIST, Imgproc.CHAIN_APPROX_NONE);
 
        for (int i = 0; i < contours.size(); i++) {
            // 计算每个轮廓的面积
            double area = Imgproc.contourArea(contours.get(i));
            // 忽略太小或太大的轮廓
            if (area < 1e2 || 1e5 < area)
                continue;
 
            // 仅为了可视化目的绘制每个轮廓
Imgproc.drawContours(src, contours, i, new Scalar(0, 0, 255), 2);
            // 查找每个形状的方向
getOrientation(contours.get(i), src);
        }

Python

contours, _ = cv.findContours(bw, cv.RETR_LIST, cv.CHAIN_APPROX_NONE)
 
for i, c in enumerate(contours)
    # 计算每个轮廓的面积
area = cv.contourArea(c)
    # 忽略过小或过大的轮廓
    if area < 1e2 or 1e5 < area
        continue
 
    # 仅为可视化目的绘制每个轮廓
    cv.drawContours(src, contours, i, (0, 0, 255), 2)
    # 查找每个形状的方向
getOrientation(c, src)

• 提取方向

通过调用 getOrientation() 函数来提取方向，该函数执行所有 PCA 过程。

C++

    // 构建 PCA 分析使用的缓冲区
    int sz = static_cast<int>(pts.size());
    Mat data_pts = Mat(sz, 2, CV_64F);
    for (int i = 0; i < data_pts.rows; i++)
    {
data_pts.at<double>(i, 0) = pts[i].x;
data_pts.at<double>(i, 1) = pts[i].y;
    }
 
    // 执行 PCA 分析
    PCA pca_analysis(data_pts, Mat(), PCA::DATA_AS_ROW);
 
    // 存储对象的中心
    Point cntr = Point(static_cast<int>(pca_analysis.mean.at<double>(0, 0)),
                      static_cast<int>(pca_analysis.mean.at<double>(0, 1)));
 
    // 存储特征值和特征向量
vector<Point2d> eigen_vecs(2);
vector<double> eigen_val(2);
    for (int i = 0; i < 2; i++)
    {
eigen_vecs[i] = Point2d(pca_analysis.eigenvectors.at<double>(i, 0),
pca_analysis.eigenvectors.at<double>(i, 1));
 
eigen_val[i] = pca_analysis.eigenvalues.at<double>(i);
    }

Java

        // Construct a buffer used by the pca analysis
        int sz = pts.size();
Mat dataPts = new Mat(sz, 2, CvType.CV_64F);
        double[] dataPtsData = new double[(int) (dataPts.total() * dataPts.channels())];
        for (int i = 0; i < dataPts.rows(); i++) {
dataPtsData[i * dataPts.cols()] = pts.get(i).x;
dataPtsData[i * dataPts.cols() + 1] = pts.get(i).y;
        }
dataPts.put(0, 0, dataPtsData);
 
        // 执行 PCA 分析
Mat mean = new Mat();
Mat eigenvectors = new Mat();
Mat eigenvalues = new Mat();
Core.PCACompute2(dataPts, mean, eigenvectors, eigenvalues);
        double[] meanData = new double[(int) (mean.total() * mean.channels())];
        mean.get(0, 0, meanData);
 
        // Store the center of the object
        Point cntr = new Point(meanData[0], meanData[1]);
 
        // Store the eigenvalues and eigenvectors
        double[] eigenvectorsData = new double[(int) (eigenvectors.total() * eigenvectors.channels())];
        double[] eigenvaluesData = new double[(int) (eigenvalues.total() * eigenvalues.channels())];
eigenvectors.get(0, 0, eigenvectorsData);
eigenvalues.get(0, 0, eigenvaluesData);

Python

sz = len(pts)
data_pts = np.empty((sz, 2), dtype=np.float64)
    for i in range(data_pts.shape[0])
data_pts[i,0] = pts[i,0,0]
data_pts[i,1] = pts[i,0,1]
 
    # 执行 PCA 分析
mean = np.empty((0))
mean, eigenvectors, eigenvalues = cv.PCACompute2(data_pts, mean)
 
    # Store the center of the object
cntr = (int(mean[0,0]), int(mean[0,1]))

首先，数据需要排列成大小为 n x 2 的矩阵，其中 n 是我们拥有的数据点数量。然后我们可以执行 PCA 分析。计算出的均值（即质心）存储在 cntr 变量中，特征向量和特征值存储在相应的 std::vector 中。

• 可视化结果

最终结果通过 drawAxis() 函数可视化，其中主成分以线条绘制，每个特征向量乘以其特征值并平移到均值位置。

C++

    // 绘制主成分
    circle(img, cntr, 3, Scalar(255, 0, 255), 2);
    Point p1 = cntr + 0.02 * Point(static_cast<int>(eigen_vecs[0].x * eigen_val[0]), static_cast<int>(eigen_vecs[0].y * eigen_val[0]));
    Point p2 = cntr - 0.02 * Point(static_cast<int>(eigen_vecs[1].x * eigen_val[1]), static_cast<int>(eigen_vecs[1].y * eigen_val[1]));
drawAxis(img, cntr, p1, Scalar(0, 255, 0), 1);
drawAxis(img, cntr, p2, Scalar(255, 255, 0), 5);
 
    double angle = atan2(eigen_vecs[0].y, eigen_vecs[0].x); // 方向（弧度）

Java

        // 绘制主成分
Imgproc.circle(img, cntr, 3, new Scalar(255, 0, 255), 2);
        Point p1 = new Point(cntr.x + 0.02 * eigenvectorsData[0] * eigenvaluesData[0],
cntr.y + 0.02 * eigenvectorsData[1] * eigenvaluesData[0]);
        Point p2 = new Point(cntr.x - 0.02 * eigenvectorsData[2] * eigenvaluesData[1],
cntr.y - 0.02 * eigenvectorsData[3] * eigenvaluesData[1]);
drawAxis(img, cntr, p1, new Scalar(0, 255, 0), 1);
drawAxis(img, cntr, p2, new Scalar(255, 255, 0), 5);
 
        double angle = Math.atan2(eigenvectorsData[1], eigenvectorsData[0]); // 方向（弧度）

Python

    cv.circle(img, cntr, 3, (255, 0, 255), 2)
p1 = (cntr[0] + 0.02 * eigenvectors[0,0] * eigenvalues[0,0], cntr[1] + 0.02 * eigenvectors[0,1] * eigenvalues[0,0])
p2 = (cntr[0] - 0.02 * eigenvectors[1,0] * eigenvalues[1,0], cntr[1] - 0.02 * eigenvectors[1,1] * eigenvalues[1,0])
drawAxis(img, cntr, p1, (0, 255, 0), 1)
drawAxis(img, cntr, p2, (255, 255, 0), 5)
 
angle = atan2(eigenvectors[0,1], eigenvectors[0,0]) # 方向（弧度）

C++

    double angle = atan2( (double) p.y - q.y, (double) p.x - q.x ); // 角度（弧度）
    double hypotenuse = sqrt( (double) (p.y - q.y) * (p.y - q.y) + (p.x - q.x) * (p.x - q.x));
 
    // 这里我们将箭头长度缩放 scale 倍
q.x = (int) (p.x - scale * hypotenuse * cos(angle));
q.y = (int) (p.y - scale * hypotenuse * sin(angle));
    line(img, p, q, colour, 1, LINE_AA);
 
    // 创建箭头钩
p.x = (int) (q.x + 9 * cos(angle + CV_PI / 4));
p.y = (int) (q.y + 9 * sin(angle + CV_PI / 4));
    line(img, p, q, colour, 1, LINE_AA);
 
p.x = (int) (q.x + 9 * cos(angle - CV_PI / 4));
p.y = (int) (q.y + 9 * sin(angle - CV_PI / 4));
    line(img, p, q, colour, 1, LINE_AA);

Java

        double angle = Math.atan2(p.y - q.y, p.x - q.x); // 角度（弧度）
        double hypotenuse = Math.sqrt((p.y - q.y) * (p.y - q.y) + (p.x - q.x) * (p.x - q.x));
 
        // 这里我们将箭头长度缩放 scale 倍
q.x = (int) (p.x - scale * hypotenuse * Math.cos(angle));
q.y = (int) (p.y - scale * hypotenuse * Math.sin(angle));
Imgproc.line(img, p, q, colour, 1, Imgproc.LINE_AA, 0);
 
        // 创建箭头钩
p.x = (int) (q.x + 9 * Math.cos(angle + Math.PI / 4));
p.y = (int) (q.y + 9 * Math.sin(angle + Math.PI / 4));
Imgproc.line(img, p, q, colour, 1, Imgproc.LINE_AA, 0);
 
p.x = (int) (q.x + 9 * Math.cos(angle - Math.PI / 4));
p.y = (int) (q.y + 9 * Math.sin(angle - Math.PI / 4));
Imgproc.line(img, p, q, colour, 1, Imgproc.LINE_AA, 0);

Python

angle = atan2(p[1] - q[1], p[0] - q[0]) # 角度（弧度）
hypotenuse = sqrt((p[1] - q[1]) * (p[1] - q[1]) + (p[0] - q[0]) * (p[0] - q[0]))
 
    # 在此处我们将箭头按比例因子加长
q[0] = p[0] - scale * hypotenuse * cos(angle)
q[1] = p[1] - scale * hypotenuse * sin(angle)
    cv.line(img, (int(p[0]), int(p[1])), (int(q[0]), int(q[1])), colour, 1, cv.LINE_AA)
 
    # 创建箭头倒钩
p[0] = q[0] + 9 * cos(angle + pi / 4)
p[1] = q[1] + 9 * sin(angle + pi / 4)
    cv.line(img, (int(p[0]), int(p[1])), (int(q[0]), int(q[1])), colour, 1, cv.LINE_AA)
 
p[0] = q[0] + 9 * cos(angle - pi / 4)
p[1] = q[1] + 9 * sin(angle - pi / 4)
    cv.line(img, (int(p[0]), int(p[1])), (int(q[0]), int(q[1])), colour, 1, cv.LINE_AA)

结果

该代码打开一幅图像，查找检测到的感兴趣对象的方向，然后通过绘制检测到的感兴趣对象的轮廓、中心点以及与提取方向相关的 x 轴和 y 轴来可视化结果。