改变图像的对比度和亮度！

目录

• 目标
• 理论
  • 图像处理
  • 像素变换
  • 亮度与对比度调整
• 代码
• 解释
• 结果
• 实际示例
  • 亮度与对比度调整
  • 伽马校正
  • 校正曝光不足的图像
  • 代码
  • 附加资源

上一个教程： 使用OpenCV添加（混合）两幅图像
下一个教程： 离散傅里叶变换

原始作者	Ana Huamán
兼容性	OpenCV >= 3.0

目标

在本教程中，您将学习如何

• 访问像素值
• 用零初始化矩阵
• 了解 cv::saturate_cast 的作用以及为何有用
• 获取一些关于像素变换的重要信息
• 在实际示例中提升图像亮度

理论

注意

下面的解释摘自 Richard Szeliski 的著作 计算机视觉：算法与应用

图像处理

• 一般的图像处理运算符是一个函数，它接受一个或多个输入图像并生成一个输出图像。
• 图像变换可视为
  • 点运算符（像素变换）
  • 邻域（基于区域）运算符

像素变换

• 在这类图像处理变换中，每个输出像素的值仅取决于相应的输入像素值（此外，可能还有一些全局收集的信息或参数）。
• 此类运算符的示例包括亮度与对比度调整以及色彩校正和变换。

亮度与对比度调整

• 两种常用的点处理是与常数进行乘法和加法运算

  \[g(x) = \alpha f(x) + \beta\]

• 参数 \(\alpha > 0\) 和 \(\beta\) 通常被称为增益和偏置参数；有时这些参数被认为分别控制对比度和亮度。

• 您可以将 \(f(x)\) 视为源图像像素，将 \(g(x)\) 视为输出图像像素。然后，我们可以更方便地将表达式写为

  \[g(i,j) = \alpha \cdot f(i,j) + \beta\]

  其中 \(i\) 和 \(j\) 表示像素位于第 i 行和第 j 列。

代码

C++

• 可下载代码：点击此处
• 以下代码执行操作 \(g(i,j) = \alpha \cdot f(i,j) + \beta\)

   
  #include "opencv2/imgcodecs.hpp"
  #include "opencv2/highgui.hpp"
  #include <iostream>
   
  // we're NOT "using namespace std;" here, to avoid collisions between the beta variable and std::beta in c++17
  using std::cin;
  using std::cout;
  using std::endl;
  using namespace cv;
   
  int main( int argc, char** argv )
  {
      CommandLineParser parser( argc, argv, "{@input | lena.jpg | input image}" );
      Mat image = imread( samples::findFile( parser.get<String>( "@input" ) ) );
      if( image.empty() )
      {
  cout << "无法打开或找到图像！\n" << endl;
  cout << "用法: " << argv[0] << " " << endl;
        return -1;
      }
   
      Mat new_image = Mat::zeros( image.size(), image.type() );
   
      double alpha = 1.0; /*< 简单对比度控制 */
      int beta = 0; /*< 简单亮度控制 */
   
  cout << " 基本线性变换 " << endl;
  cout << "-------------------------" << endl;
  cout << "* 输入 alpha 值 [1.0-3.0]: "; cin >> alpha;
  cout << "* 输入 beta 值 [0-100]: "; cin >> beta;
   
      for( int y = 0; y < image.rows; y++ ) {
          for( int x = 0; x < image.cols; x++ ) {
              for( int c = 0; c < image.channels(); c++ ) {
  new_image.at<Vec3b>(y,x)[c] =
  saturate_cast<uchar>( alpha*image.at<Vec3b>(y,x)[c] + beta );
              }
          }
      }
   
      imshow("原始图像", image);
      imshow("新图像", new_image);
   
      waitKey();
      return 0;
  }

Java

• 可下载代码：点击此处
• 以下代码执行操作 \(g(i,j) = \alpha \cdot f(i,j) + \beta\)

  import java.util.Scanner;
   
  import org.opencv.core.Core;
  import org.opencv.core.Mat;
  import org.opencv.highgui.HighGui;
  import org.opencv.imgcodecs.Imgcodecs;
   
  class BasicLinearTransforms {
      private byte saturate(double val) {
          int iVal = (int) Math.round(val);
  iVal = iVal > 255 ? 255 : (iVal < 0 ? 0 : iVal);
          return (byte) iVal;
      }
   
      public void run(String[] args) {
  String imagePath = args.length > 0 ? args[0] : "../data/lena.jpg";
  Mat image = Imgcodecs.imread(imagePath);
          if (image.empty()) {
  System.out.println("图像为空: " + imagePath);
  System.exit(0);
          }
   
  Mat newImage = Mat.zeros(image.size(), image.type());
   
          double alpha = 1.0; /*< 简单对比度控制 */
          int beta = 0; /*< 简单亮度控制 */
   
  System.out.println(" 基本线性变换 ");
  System.out.println("-------------------------");
          try (Scanner scanner = new Scanner(System.in)) {
  System.out.print("* 输入 alpha 值 [1.0-3.0]: ");
  alpha = scanner.nextDouble();
  System.out.print("* 输入 beta 值 [0-100]: ");
  beta = scanner.nextInt();
          }
   
          byte[] imageData = new byte[(int) (image.total()*image.channels())];
  image.get(0, 0, imageData);
          byte[] newImageData = new byte[(int) (newImage.total()*newImage.channels())];
          for (int y = 0; y < image.rows(); y++) {
              for (int x = 0; x < image.cols(); x++) {
                  for (int c = 0; c < image.channels(); c++) {
                      double pixelValue = imageData[(y * image.cols() + x) * image.channels() + c];
  pixelValue = pixelValue < 0 ? pixelValue + 256 : pixelValue;
  newImageData[(y * image.cols() + x) * image.channels() + c]
  = saturate(alpha * pixelValue + beta);
                  }
              }
          }
  newImage.put(0, 0, newImageData);
   
  HighGui.imshow("原始图像", image);
  HighGui.imshow("新图像", newImage);
   
  HighGui.waitKey();
  System.exit(0);
      }
  }
   
  public class BasicLinearTransformsDemo {
      public static void main(String[] args) {
          // 加载本地 OpenCV 库
  System.loadLibrary(Core.NATIVE_LIBRARY_NAME);
   
          new BasicLinearTransforms().run(args);
      }
  }

Python

• 可下载代码：点击此处
• 以下代码执行操作 \(g(i,j) = \alpha \cdot f(i,j) + \beta\)

  from __future__ import print_function
  from builtins import input
  import cv2 as cv
  import numpy as np
  import argparse
   
  # 读取用户提供的图像
   
  parser = argparse.ArgumentParser(description='用于改变图像对比度和亮度的代码！教程。');
  parser.add_argument('--input', help='输入图像的路径。', default='lena.jpg')
  args = parser.parse_args()
   
  image = cv.imread(cv.samples.findFile(args.input))
  if image is None
  print('无法打开或找到图像：', args.input)
  exit(0)
   
   
   
  new_image = np.zeros(image.shape, image.dtype)
   
   
   
  alpha = 1.0 # 简单对比度控制
  beta = 0 # 简单亮度控制
   
  # 初始化值
  print(' 基本线性变换 ')
  print('-------------------------')
  try:
  alpha = float(input('* 输入 alpha 值 [1.0-3.0]: '))
  beta = int(input('* 输入 beta 值 [0-100]: '))
  except ValueError
  print('错误，不是数字')
   
   
  # 执行操作 new_image(i,j) = alpha*image(i,j) + beta
  # 除了这些 'for' 循环，我们也可以简单地使用
  # new_image = cv.convertScaleAbs(image, alpha=alpha, beta=beta)
  # 但我们想向你展示如何访问像素 :)
   
  for y in range(image.shape[0])
      for x in range(image.shape[1])
          for c in range(image.shape[2])
  new_image[y,x,c] = np.clip(alpha*image[y,x,c] + beta, 0, 255)
   
   
   
  cv.imshow("原始图像", image)
  cv.imshow("新图像", new_image)
   
  # Wait until user press some key
  cv.waitKey()
   

解释

• 我们使用 cv::imread 加载图像并将其保存到 Mat 对象中

C++

    CommandLineParser parser( argc, argv, "{@input | lena.jpg | input image}" );
    Mat image = imread( samples::findFile( parser.get<String>( "@input" ) ) );
    if( image.empty() )
    {
cout << "无法打开或找到图像！\n" << endl;
cout << "用法: " << argv[0] << " " << endl;
      return -1;
    }

Java

        String imagePath = args.length > 0 ? args[0] : "../data/lena.jpg";
Mat image = Imgcodecs.imread(imagePath);
        if (image.empty()) {
System.out.println("图像为空: " + imagePath);
System.exit(0);
        }

Python

parser = argparse.ArgumentParser(description='用于改变图像对比度和亮度的代码！教程。');
parser.add_argument('--input', help='输入图像的路径。', default='lena.jpg')
args = parser.parse_args()
 
image = cv.imread(cv.samples.findFile(args.input))
if image is None
print('无法打开或找到图像：', args.input)
exit(0)

• 现在，由于我们将对该图像进行一些变换，我们需要一个新的 Mat 对象来存储它。此外，我们希望它具有以下特点：
  • 初始像素值等于零
  • 与原始图像相同的大小和类型

C++

    Mat new_image = Mat::zeros( image.size(), image.type() );

Java

Mat newImage = Mat.zeros(image.size(), image.type());

Python

new_image = np.zeros(image.shape, image.dtype)

我们观察到 cv::Mat::zeros 根据 image.size() 和 image.type() 返回一个 Matlab 风格的零初始化器

• 现在，我们要求用户输入 \(\alpha\) 和 \(\beta\) 的值

C++

    double alpha = 1.0; /*< 简单对比度控制 */
    int beta = 0; /*< 简单亮度控制 */
 
cout << " 基本线性变换 " << endl;
cout << "-------------------------" << endl;
cout << "* 输入 alpha 值 [1.0-3.0]: "; cin >> alpha;
cout << "* 输入 beta 值 [0-100]: "; cin >> beta;

Java

        double alpha = 1.0; /*< 简单对比度控制 */
        int beta = 0; /*< 简单亮度控制 */
 
System.out.println(" 基本线性变换 ");
System.out.println("-------------------------");
        try (Scanner scanner = new Scanner(System.in)) {
System.out.print("* 输入 alpha 值 [1.0-3.0]: ");
alpha = scanner.nextDouble();
System.out.print("* 输入 beta 值 [0-100]: ");
beta = scanner.nextInt();
        }

Python

alpha = 1.0 # 简单对比度控制
beta = 0 # 简单亮度控制
 
# 初始化值
print(' 基本线性变换 ')
print('-------------------------')
try:
alpha = float(input('* 输入 alpha 值 [1.0-3.0]: '))
beta = int(input('* 输入 beta 值 [0-100]: '))
except ValueError
print('错误，不是数字')

• 现在，为了执行操作 \(g(i,j) = \alpha \cdot f(i,j) + \beta\)，我们将访问图像中的每个像素。由于我们处理的是 BGR 图像，每个像素将有三个值（B、G 和 R），因此我们也将单独访问它们。以下是代码片段：

C++

    for( int y = 0; y < image.rows; y++ ) {
        for( int x = 0; x < image.cols; x++ ) {
            for( int c = 0; c < image.channels(); c++ ) {
new_image.at<Vec3b>(y,x)[c] =
saturate_cast<uchar>( alpha*image.at<Vec3b>(y,x)[c] + beta );
            }
        }
    }

Java

        byte[] imageData = new byte[(int) (image.total()*image.channels())];
image.get(0, 0, imageData);
        byte[] newImageData = new byte[(int) (newImage.total()*newImage.channels())];
        for (int y = 0; y < image.rows(); y++) {
            for (int x = 0; x < image.cols(); x++) {
                for (int c = 0; c < image.channels(); c++) {
                    double pixelValue = imageData[(y * image.cols() + x) * image.channels() + c];
pixelValue = pixelValue < 0 ? pixelValue + 256 : pixelValue;
newImageData[(y * image.cols() + x) * image.channels() + c]
= saturate(alpha * pixelValue + beta);
                }
            }
        }
newImage.put(0, 0, newImageData);

Python

for y in range(image.shape[0])
    for x in range(image.shape[1])
        for c in range(image.shape[2])
new_image[y,x,c] = np.clip(alpha*image[y,x,c] + beta, 0, 255)

请注意以下内容（仅限 C++ 代码）

• 要访问图像中的每个像素，我们使用以下语法：image.at<Vec3b>(y,x)[c]，其中 y 是行，x 是列，c 是 B、G 或 R（0、1 或 2）。
• 由于操作 \(\alpha \cdot p(i,j) + \beta\) 可能会给出超出范围的值或非整数值（如果 \(\alpha\) 是浮点数），我们使用 cv::saturate_cast 来确保值的有效性。
• 最后，我们以通常的方式创建窗口并显示图像。

C++

    imshow("原始图像", image);
    imshow("新图像", new_image);
 
    waitKey();

Java

HighGui.imshow("原始图像", image);
HighGui.imshow("新图像", newImage);
 
HighGui.waitKey();

Python

cv.imshow("原始图像", image)
cv.imshow("新图像", new_image)
 
# Wait until user press some key
cv.waitKey()

注意

除了使用 for 循环来访问每个像素，我们也可以简单地使用以下命令：

C++

image.convertTo(new_image, -1, alpha, beta);

Java

image.convertTo(newImage, -1, alpha, beta);

Python

new_image = cv.convertScaleAbs(image, alpha=alpha, beta=beta)

其中 cv::Mat::convertTo 会有效地执行 *new_image = a*image + beta*。然而，我们想向你展示如何访问每个像素。无论如何，这两种方法都给出相同的结果，但 convertTo 更优化，运行速度快得多。

结果

• 运行我们的代码，并使用 \(\alpha = 2.2\) 和 \(\beta = 50\)

  $ ./BasicLinearTransforms lena.jpg
  基本线性变换
  -------------------------
  * 输入 alpha 值 [1.0-3.0]: 2.2
  * 输入 beta 值 [0-100]: 50

• 我们得到以下结果：

实际示例

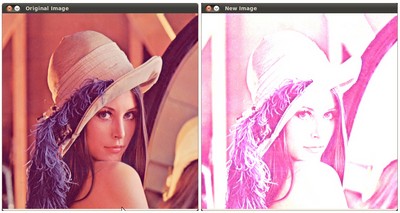
在本段中，我们将学到的知识付诸实践，通过调整图像的亮度和对比度来校正曝光不足的图像。我们还将介绍另一种校正图像亮度的技术，称为伽马校正。

亮度与对比度调整

增加（/减少）\(\beta\) 值将为每个像素添加（/减去）一个常数值。超出 [0 ; 255] 范围的像素值将被饱和（即，高于 255（/低于 0）的像素值将被限制在 255（/0））。

浅灰色为原始图像的直方图，深灰色为 Gimp 中亮度设为 80 时的直方图

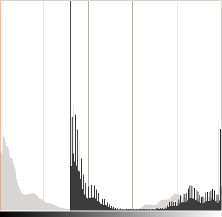
直方图表示每个颜色级别拥有该颜色级别的像素数量。黑暗图像会有许多颜色值较低的像素，因此直方图会在其左侧呈现一个峰值。当添加一个常数偏置时，由于我们为所有像素添加了一个常数偏置，直方图会向右移动。

\(\alpha\) 参数将改变色阶的分布方式。如果 \( \alpha < 1 \)，色阶将被压缩，结果将是对比度较低的图像。

浅灰色为原始图像的直方图，深灰色为 Gimp 中对比度设为 < 0 时的直方图

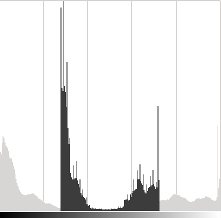
请注意，这些直方图是使用 Gimp 软件中的亮度-对比度工具获得的。亮度工具应该与 \(\beta\) 偏置参数相同，但对比度工具似乎与 \(\alpha\) 增益不同，在 Gimp 中输出范围似乎是居中的（正如您可以在之前的直方图中注意到的）。

可能会出现这样的情况：调整 \(\beta\) 偏置会改善亮度，但同时图像会显得略带蒙版，因为对比度会降低。使用 \(\alpha\) 增益可以减弱这种效果，但由于饱和度，我们将在原始亮部区域丢失一些细节。

伽马校正

伽马校正 可通过输入值与映射输出值之间的非线性变换来校正图像的亮度

\[O = \left( \frac{I}{255} \right)^{\gamma} \times 255\]

由于这种关系是非线性的，其效果对所有像素并非相同，而是取决于它们的原始值。

不同伽马值对应的曲线图

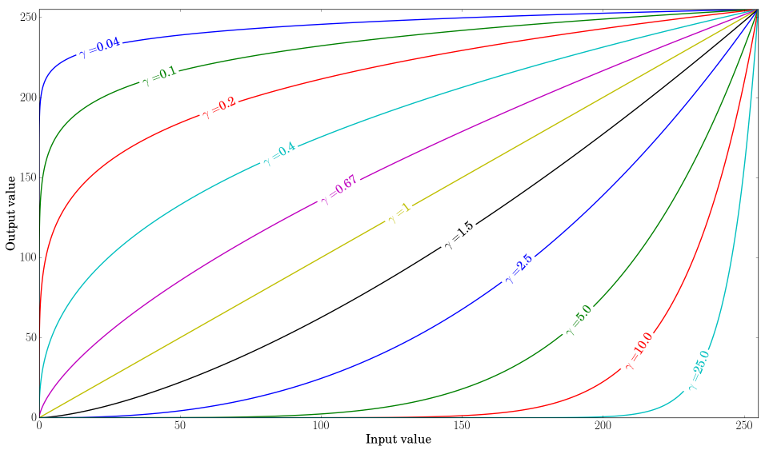
当 \( \gamma < 1 \) 时，原始暗部区域会更亮，直方图将向右移动；而当 \( \gamma > 1 \) 时，效果则相反。

校正曝光不足的图像

以下图像已使用 \( \alpha = 1.3 \) 和 \( \beta = 40 \) 进行校正。

由 Visem（自己的作品）[CC BY-SA 3.0]，通过维基共享资源

整体亮度得到了改善，但您可能会注意到，由于所用实现中的数值饱和（摄影中的高光裁剪），云彩现在严重饱和。

以下图像已使用 \( \gamma = 0.4 \) 进行校正。

由 Visem（自己的作品）[CC BY-SA 3.0]，通过维基共享资源

伽马校正应该会减少饱和效果，因为映射是非线性的，并且不像之前的方法那样可能出现数值饱和。

左：经过 alpha, beta 校正后的直方图；中：原始图像的直方图；右：经过伽马校正后的直方图

上图比较了三幅图像的直方图（三个直方图的 Y 轴范围不同）。您可以注意到，原始图像的大部分像素值都集中在直方图的低端。经过 \( \alpha \), \( \beta \) 校正后，由于饱和以及向右的偏移，我们可以在 255 处观察到一个大峰值。经过伽马校正后，直方图向右移动，但暗部区域的像素比亮部区域的像素移动得更多（参见伽马曲线图）。

在本教程中，您已经学习了两种调整图像对比度和亮度的简单方法。它们是基本技术，并非旨在取代光栅图形编辑器！

代码

C++

教程代码在此。

Java

教程代码在此。

Python

教程代码在此。

伽马校正代码

C++

    Mat lookUpTable(1, 256, CV_8U);
    uchar* p = lookUpTable.ptr();
    for( int i = 0; i < 256; ++i)
p[i] = saturate_cast<uchar>(pow(i / 255.0, gamma_) * 255.0);
 
    Mat res = img.clone();
    LUT(img, lookUpTable, res);

Java

Mat lookUpTable = new Mat(1, 256, CvType.CV_8U);
        byte[] lookUpTableData = new byte[(int) (lookUpTable.total()*lookUpTable.channels())];
        for (int i = 0; i < lookUpTable.cols(); i++) {
lookUpTableData[i] = saturate(Math.pow(i / 255.0, gammaValue) * 255.0);
        }
lookUpTable.put(0, 0, lookUpTableData);
Mat img = new Mat();
Core.LUT(matImgSrc, lookUpTable, img);

Python

lookUpTable = np.empty((1,256), np.uint8)
    for i in range(256)
lookUpTable[0,i] = np.clip(pow(i / 255.0, gamma) * 255.0, 0, 255)
 
res = cv.LUT(img_original, lookUpTable)

查找表用于提高计算性能，因为只需计算一次 256 个值。

附加资源

• 图形渲染中的伽马校正
• 伽马校正与在 CRT 显示器上显示的图像
• 数字曝光技术