光流

目录

• 目标
• 光流
  • Lucas-Kanade 方法
• OpenCV 中的 Lucas-Kanade 光流
• OpenCV 中的稠密光流

上一个教程： 均值漂移和 Camshift
下一个教程： 级联分类器

目标

在本章中，

• 我们将理解光流的概念及其使用 Lucas-Kanade 方法进行估计。
• 我们将使用 cv.calcOpticalFlowPyrLK() 等函数来跟踪视频中的特征点。
• 我们将使用 cv.calcOpticalFlowFarneback() 方法创建一个稠密光流场。

光流

光流是图像对象在连续两帧之间由于物体或摄像机运动而产生的表观运动模式。它是一个二维向量场，其中每个向量都是一个位移向量，显示了点从第一帧到第二帧的移动。考虑下图（图片来源：维基百科光流文章）。

image

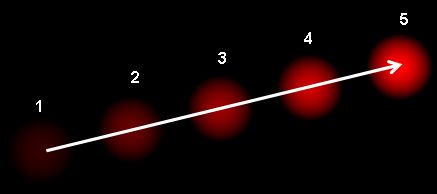
它显示了一个球在5个连续帧中的运动。箭头显示了它的位移向量。光流在许多领域都有应用，例如

• 从运动中恢复结构
• 视频压缩
• 视频稳定 ...

光流基于以下几个假设：

1. 对象的像素强度在连续帧之间不会改变。
2. 相邻像素具有相似的运动。

考虑第一帧中的像素 \(I(x,y,t)\)（注意，这里添加了一个新维度：时间。之前我们只处理图像，所以不需要时间）。它在 \(dt\) 时间后的下一帧中移动了距离 \((dx,dy)\)。因此，由于这些像素是相同的且强度不变，我们可以说，

\[I(x,y,t) = I(x+dx, y+dy, t+dt)\]

然后对右侧进行泰勒级数近似，去掉相同项并除以 \(dt\)，得到以下方程

\[f_x u + f_y v + f_t = 0 \;\]

其中

\[f_x = \frac{\partial f}{\partial x} \; ; \; f_y = \frac{\partial f}{\partial y}\]

\[u = \frac{dx}{dt} \; ; \; v = \frac{dy}{dt}\]

上述方程称为光流方程。在其中，我们可以找到 \(f_x\) 和 \(f_y\)，它们是图像梯度。类似地，\(f_t\) 是沿时间的梯度。但 \((u,v)\) 是未知量。我们无法用两个未知变量求解这个方程。因此，提供了几种方法来解决这个问题，其中之一就是 Lucas-Kanade 方法。

Lucas-Kanade 方法

我们之前见过一个假设，即所有相邻像素将具有相似的运动。Lucas-Kanade 方法在点周围取一个 3x3 的图像块。因此，所有 9 个点都具有相同的运动。我们可以找到这 9 个点的 \((f_x, f_y, f_t)\)。所以现在我们的问题变成了求解一个包含两个未知变量的 9 个方程组，这是一个超定系统。使用最小二乘拟合方法可以获得更好的解决方案。下面是最终的解决方案，它是一个二方程两未知量问题，求解即可得到答案。

\[\begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} \sum_{i}{f_{x_i}}^2 & \sum_{i}{f_{x_i} f_{y_i} } \\ \sum_{i}{f_{x_i} f_{y_i}} & \sum_{i}{f_{y_i}}^2 \end{bmatrix}^{-1} \begin{bmatrix} - \sum_{i}{f_{x_i} f_{t_i}} \\ - \sum_{i}{f_{y_i} f_{t_i}} \end{bmatrix}\]

（检查逆矩阵与 Harris 角点检测器的相似性。它表明角点是更好的跟踪点。）

因此，从用户角度来看，这个想法很简单，我们提供一些点来跟踪，然后接收这些点的光流向量。但仍然存在一些问题。到目前为止，我们只处理小范围运动，因此当运动幅度较大时，它会失效。为了解决这个问题，我们使用金字塔。当我们沿着金字塔向上时，小范围运动会被消除，大范围运动会变成小范围运动。因此，通过在那里应用 Lucas-Kanade 方法，我们可以获得光流以及尺度信息。

OpenCV 中的 Lucas-Kanade 光流

OpenCV 将所有这些功能集成在一个函数中：cv.calcOpticalFlowPyrLK()。在这里，我们创建一个简单的应用程序来跟踪视频中的某些点。为了确定这些点，我们使用 cv.goodFeaturesToTrack()。我们获取第一帧，在其中检测一些 Shi-Tomasi 角点，然后使用 Lucas-Kanade 光流迭代跟踪这些点。对于函数 cv.calcOpticalFlowPyrLK()，我们传入前一帧、前一个点和下一帧。它返回下一个点以及一些状态数字，如果找到下一个点，则状态值为 1，否则为 0。我们迭代地将这些下一个点作为前一个点在下一步中传递。请参阅下面的代码。

C++

• 可下载代码：点击此处
• 代码速览

  #include <iostream>
  #include <opencv2/core.hpp>
  #include <opencv2/highgui.hpp>
  #include <opencv2/imgproc.hpp>
  #include <opencv2/videoio.hpp>
  #include <opencv2/video.hpp>
   
  using namespace cv;
  using namespace std;
   
  int main(int argc, char **argv)
  {
      const string about =
          "This sample demonstrates Lucas-Kanade Optical Flow calculation.\n"
          "The example file can be downloaded from:\n"
          " https://www.bogotobogo.com/python/OpenCV_Python/images/mean_shift_tracking/slow_traffic_small.mp4";
      const string keys =
          "{ h help | | 打印此帮助消息 }"
          "{ @image | vtest.avi | path to image file }";
      CommandLineParser parser(argc, argv, keys);
  parser.about(about);
      if (parser.has("help"))
      {
  parser.printMessage();
          return 0;
      }
      string filename = samples::findFile(parser.get<string>("@image"));
      if (!parser.check())
      {
  parser.printErrors();
          return 0;
      }
   
      VideoCapture capture(filename);
      if (!capture.isOpened()){
          //error in opening the video input
  cerr << "Unable to open file!" << endl;
          return 0;
      }
   
      // Create some random colors
  vector<Scalar> colors;
      RNG rng;
      for(int i = 0; i < 100; i++)
      {
          int r = rng.uniform(0, 256);
          int g = rng.uniform(0, 256);
          int b = rng.uniform(0, 256);
  colors.emplace_back(r,g,b);
      }
   
      Mat old_frame, old_gray;
  vector<Point2f> p0, p1;
   
      // Take first frame and find corners in it
  capture >> old_frame;
      cvtColor(old_frame, old_gray, COLOR_BGR2GRAY);
      goodFeaturesToTrack(old_gray, p0, 100, 0.3, 7, Mat(), 7, false, 0.04);
   
      // Create a mask image for drawing purposes
      Mat mask = Mat::zeros(old_frame.size(), old_frame.type());
   
      while(true){
          Mat frame, frame_gray;
   
  capture >> frame;
          if (frame.empty())
              break;
          cvtColor(frame, frame_gray, COLOR_BGR2GRAY);
   
          // calculate optical flow
  vector<uchar> status;
  vector<float> err;
          TermCriteria criteria = TermCriteria((TermCriteria::COUNT) + (TermCriteria::EPS), 10, 0.03);
          calcOpticalFlowPyrLK(old_gray, frame_gray, p0, p1, status, err, Size(15,15), 2, criteria);
   
  vector<Point2f> good_new;
          for(uint i = 0; i < p0.size(); i++)
          {
              // Select good points
              if(status[i] == 1) {
  good_new.push_back(p1[i]);
                  // draw the tracks
                  line(mask,p1[i], p0[i], colors[i], 2);
                  circle(frame, p1[i], 5, colors[i], -1);
              }
          }
          Mat img;
          add(frame, mask, img);
   
          imshow("Frame", img);
   
          int keyboard = waitKey(30);
          if (keyboard == 'q' || keyboard == 27)
              break;
   
          // Now update the previous frame and previous points
  old_gray = frame_gray.clone();
  p0 = good_new;
      }
  }

Python

• 可下载代码：点击此处
• 代码速览

  import numpy as np
  import cv2 as cv
  import argparse
   
  parser = argparse.ArgumentParser(description='This sample demonstrates Lucas-Kanade Optical Flow calculation. \
  The example file can be downloaded from: \
  https://www.bogotobogo.com/python/OpenCV_Python/images/mean_shift_tracking/slow_traffic_small.mp4')
  parser.add_argument('image', type=str, help='path to image file')
  args = parser.parse_args()
   
  cap = cv.VideoCapture(args.image)
   
  # params for ShiTomasi corner detection
  feature_params = dict( maxCorners = 100,
  qualityLevel = 0.3,
  minDistance = 7,
  blockSize = 7 )
   
  # Parameters for lucas kanade optical flow
  lk_params = dict( winSize = (15, 15),
  maxLevel = 2,
  criteria = (cv.TERM_CRITERIA_EPS | cv.TERM_CRITERIA_COUNT, 10, 0.03))
   
  # Create some random colors
  color = np.random.randint(0, 255, (100, 3))
   
  # Take first frame and find corners in it
  ret, old_frame = cap.read()
  old_gray = cv.cvtColor(old_frame, cv.COLOR_BGR2GRAY)
  p0 = cv.goodFeaturesToTrack(old_gray, mask = None, **feature_params)
   
  # Create a mask image for drawing purposes
  mask = np.zeros_like(old_frame)
   
  while(1)
  ret, frame = cap.read()
      if not ret
  print('No frames grabbed!')
          break
   
  frame_gray = cv.cvtColor(frame, cv.COLOR_BGR2GRAY)
   
      # calculate optical flow
  p1, st, err = cv.calcOpticalFlowPyrLK(old_gray, frame_gray, p0, None, **lk_params)
   
      # Select good points
      if p1 is not None
  good_new = p1[st==1]
  good_old = p0[st==1]
   
      # draw the tracks
      for i, (new, old) in enumerate(zip(good_new, good_old))
  a, b = new.ravel()
  c, d = old.ravel()
  mask = cv.line(mask, (int(a), int(b)), (int(c), int(d)), color[i].tolist(), 2)
  frame = cv.circle(frame, (int(a), int(b)), 5, color[i].tolist(), -1)
  img = cv.add(frame, mask)
   
      cv.imshow('frame', img)
  k = cv.waitKey(30) & 0xff
      if k == 27
          break
   
      # Now update the previous frame and previous points
  old_gray = frame_gray.copy()
  p0 = good_new.reshape(-1, 1, 2)
   
  cv.destroyAllWindows()

Java

• 可下载代码：点击此处
• 代码速览

  import java.util.ArrayList;
  import java.util.Random;
  import org.opencv.core.*;
  import org.opencv.highgui.HighGui;
  import org.opencv.imgproc.Imgproc;
  import org.opencv.video.Video;
  import org.opencv.videoio.VideoCapture;
   
  class OptFlow {
      public void run(String[] args) {
  String filename = args[0];
  VideoCapture capture = new VideoCapture(filename);
          if (!capture.isOpened()) {
  System.out.println("Unable to open this file");
  System.exit(-1);
          }
   
   
          // Create some random colors
  Scalar[] colors = new Scalar[100];
  Random rng = new Random();
          for (int i = 0 ; i < 100 ; i++) {
              int r = rng.nextInt(256);
              int g = rng.nextInt(256);
              int b = rng.nextInt(256);
  colors[i] = new Scalar(r, g, b);
          }
   
  Mat old_frame = new Mat() , old_gray = new Mat();
   
          // Since the function Imgproc.goodFeaturesToTrack requires MatofPoint
          // therefore first p0MatofPoint is passed to the function and then converted to MatOfPoint2f
  MatOfPoint p0MatofPoint = new MatOfPoint();
  capture.read(old_frame);
  Imgproc.cvtColor(old_frame, old_gray, Imgproc.COLOR_BGR2GRAY);
  Imgproc.goodFeaturesToTrack(old_gray, p0MatofPoint,100,0.3,7, new Mat(),7,false,0.04);
   
  MatOfPoint2f p0 = new MatOfPoint2f(p0MatofPoint.toArray()) , p1 = new MatOfPoint2f();
   
          // Create a mask image for drawing purposes
  Mat mask = Mat.zeros(old_frame.size(), old_frame.type());
   
          while (true) {
  Mat frame = new Mat(), frame_gray = new Mat();
  capture.read(frame);
              if (frame.empty()) {
                  break;
              }
   
  Imgproc.cvtColor(frame, frame_gray, Imgproc.COLOR_BGR2GRAY);
   
              // calculate optical flow
  MatOfByte status = new MatOfByte();
  MatOfFloat err = new MatOfFloat();
  TermCriteria criteria = new TermCriteria(TermCriteria.COUNT + TermCriteria.EPS,10,0.03);
  Video.calcOpticalFlowPyrLK(old_gray, frame_gray, p0, p1, status, err, new Size(15,15),2, criteria);
   
              byte StatusArr[] = status.toArray();
  Point p0Arr[] = p0.toArray();
  Point p1Arr[] = p1.toArray();
  ArrayList<Point> good_new = new ArrayList<>();
   
              for (int i = 0; i<StatusArr.length ; i++ ) {
                  if (StatusArr[i] == 1) {
  good_new.add(p1Arr[i]);
  Imgproc.line(mask, p1Arr[i], p0Arr[i], colors[i],2);
  Imgproc.circle(frame, p1Arr[i],5, colors[i],-1);
                  }
              }
   
  Mat img = new Mat();
  Core.add(frame, mask, img);
   
  HighGui.imshow("Frame", img);
   
              int keyboard = HighGui.waitKey(30);
              if (keyboard == 'q' || keyboard == 27) {
                  break;
              }
   
              // Now update the previous frame and previous points
  old_gray = frame_gray.clone();
              Point[] good_new_arr = new Point[good_new.size()];
  good_new_arr = good_new.toArray(good_new_arr);
  p0 = new MatOfPoint2f(good_new_arr);
          }
  System.exit(0);
      }
  }
   
  public class OpticalFlowDemo {
      public static void main(String[] args) {
  System.loadLibrary(Core.NATIVE_LIBRARY_NAME);
          new OptFlow().run(args);
      }
  }

（此代码不检查下一个关键点的正确性。因此，即使图像中的任何特征点消失，光流也有可能找到看起来与其接近的下一个点。所以，实际上为了进行稳健的跟踪，应该以特定的间隔检测角点。OpenCV 示例中包含这样一个示例，它每 5 帧查找一次特征点。它还会对获得的光流点进行反向检查，以仅选择好的点。请查看 samples/python/lk_track.py）。

查看我们得到的结果

image

OpenCV 中的稠密光流

Lucas-Kanade 方法计算稀疏特征集（在我们的示例中，是使用 Shi-Tomasi 算法检测到的角点）的光流。OpenCV 提供了另一种算法来查找稠密光流。它计算帧中所有点的光流。该算法基于 Gunnar Farneback 在 2003 年的论文《基于多项式展开的双帧运动估计》中解释的 Gunnar Farneback 算法。

以下示例展示了如何使用上述算法查找稠密光流。我们获得一个包含光流向量 \((u,v)\) 的双通道数组。我们计算它们的幅度和方向。为了更好的可视化，我们对结果进行了颜色编码。方向对应于图像的色相值。幅度对应于亮度平面。请参阅下面的代码。

C++

• 可下载代码：点击此处
• 代码速览

  #include <iostream>
  #include <opencv2/core.hpp>
  #include <opencv2/highgui.hpp>
  #include <opencv2/imgproc.hpp>
  #include <opencv2/videoio.hpp>
  #include <opencv2/video.hpp>
   
  using namespace cv;
  using namespace std;
   
  int main()
  {
      VideoCapture capture(samples::findFile("vtest.avi"));
      if (!capture.isOpened()){
          //error in opening the video input
  cerr << "Unable to open file!" << endl;
          return 0;
      }
   
      Mat frame1, prvs;
  capture >> frame1;
  cvtColor(frame1, prvs, COLOR_BGR2GRAY);
   
      while(true){
          Mat frame2, next;
  capture >> frame2;
          if (frame2.empty())
              break;
  cvtColor(frame2, next, COLOR_BGR2GRAY);
   
          Mat flow(prvs.size(), CV_32FC2);
  calcOpticalFlowFarneback(prvs, next, flow, 0.5, 3, 15, 3, 5, 1.2, 0);
   
          // visualization
          Mat flow_parts[2];
  split(flow, flow_parts);
          Mat magnitude, angle, magn_norm;
  cartToPolar(flow_parts[0], flow_parts[1], magnitude, angle, true);
  normalize(magnitude, magn_norm, 0.0f, 1.0f, NORM_MINMAX);
  angle *= ((1.f / 360.f) * (180.f / 255.f));
   
          //build hsv image
          Mat _hsv[3], hsv, hsv8, bgr;
  _hsv[0] = angle;
  _hsv[1] = Mat::ones(angle.size(), CV_32F);
  _hsv[2] = magn_norm;
  merge(_hsv, 3, hsv);
  hsv.convertTo(hsv8, CV_8U, 255.0);
  cvtColor(hsv8, bgr, COLOR_HSV2BGR);
   
  imshow("frame2", bgr);
   
          int keyboard = waitKey(30);
          if (keyboard == 'q' || keyboard == 27)
              break;
   
  prvs = next;
      }
  }

Python

• 可下载代码：点击此处
• 代码速览

  import numpy as np
  import cv2 as cv
  cap = cv.VideoCapture(cv.samples.findFile("vtest.avi"))
  ret, frame1 = cap.read()
  prvs = cv.cvtColor(frame1, cv.COLOR_BGR2GRAY)
  hsv = np.zeros_like(frame1)
  hsv[..., 1] = 255
  while(1)
  ret, frame2 = cap.read()
      if not ret
  print('No frames grabbed!')
          break
   
  next = cv.cvtColor(frame2, cv.COLOR_BGR2GRAY)
  flow = cv.calcOpticalFlowFarneback(prvs, next, None, 0.5, 3, 15, 3, 5, 1.2, 0)
  mag, ang = cv.cartToPolar(flow[..., 0], flow[..., 1])
  hsv[..., 0] = ang*180/np.pi/2
  hsv[..., 2] = cv.normalize(mag, None, 0, 255, cv.NORM_MINMAX)
  bgr = cv.cvtColor(hsv, cv.COLOR_HSV2BGR)
      cv.imshow('frame2', bgr)
  k = cv.waitKey(30) & 0xff
      if k == 27
          break
      elif k == ord('s')
          cv.imwrite('opticalfb.png', frame2)
          cv.imwrite('opticalhsv.png', bgr)
  prvs = next
   
  cv.destroyAllWindows()

Java

• 可下载代码：点击此处
• 代码速览

  import java.util.ArrayList;
  import org.opencv.core.*;
  import org.opencv.highgui.HighGui;
  import org.opencv.imgproc.Imgproc;
  import org.opencv.video.Video;
  import org.opencv.videoio.VideoCapture;
   
   
  class OptFlowDense {
      public void run(String[] args) {
  String filename = args[0];
  VideoCapture capture = new VideoCapture(filename);
          if (!capture.isOpened()) {
              //error in opening the video input
  System.out.println("Unable to open file!");
  System.exit(-1);
          }
   
  Mat frame1 = new Mat() , prvs = new Mat();
  capture.read(frame1);
  Imgproc.cvtColor(frame1, prvs, Imgproc.COLOR_BGR2GRAY);
   
          while (true) {
  Mat frame2 = new Mat(), next = new Mat();
  capture.read(frame2);
              if (frame2.empty()) {
                  break;
              }
  Imgproc.cvtColor(frame2, next, Imgproc.COLOR_BGR2GRAY);
   
  Mat flow = new Mat(prvs.size(), CvType.CV_32FC2);
  Video.calcOpticalFlowFarneback(prvs, next, flow,0.5,3,15,3,5,1.2,0);
   
              // visualization
  ArrayList<Mat> flow_parts = new ArrayList<>(2);
  Core.split(flow, flow_parts);
  Mat magnitude = new Mat(), angle = new Mat(), magn_norm = new Mat();
  Core.cartToPolar(flow_parts.get(0), flow_parts.get(1), magnitude, angle,true);
  Core.normalize(magnitude, magn_norm,0.0,1.0, Core.NORM_MINMAX);
              float factor = (float) ((1.0/360.0)*(180.0/255.0));
  Mat new_angle = new Mat();
  Core.multiply(angle, new Scalar(factor), new_angle);
   
              //build hsv image
  ArrayList<Mat> _hsv = new ArrayList<>() ;
  Mat hsv = new Mat(), hsv8 = new Mat(), bgr = new Mat();
   
  _hsv.add(new_angle);
  _hsv.add(Mat.ones(angle.size(), CvType.CV_32F));
  _hsv.add(magn_norm);
  Core.merge(_hsv, hsv);
  hsv.convertTo(hsv8, CvType.CV_8U, 255.0);
  Imgproc.cvtColor(hsv8, bgr, Imgproc.COLOR_HSV2BGR);
   
  HighGui.imshow("frame2", bgr);
   
              int keyboard = HighGui.waitKey(30);
              if (keyboard == 'q' || keyboard == 27) {
                  break;
              }
  prvs = next;
          }
  System.exit(0);
      }
  }
   
  public class OpticalFlowDenseDemo {
      public static void main(String[] args) {
  System.loadLibrary(Core.NATIVE_LIBRARY_NAME);
          new OptFlowDense().run(args);
      }
  }

请参阅下面的结果

image