目标

本教程的目标是向您展示如何使用 OpenCV parallel_for_ 框架轻松地并行化您的代码。为了说明这个概念，我们将编写一个程序来绘制曼德布罗集，充分利用几乎所有的 CPU 负载。完整的教程代码在这里。如果您想了解更多关于多线程的信息，您需要参考相关书籍或课程，因为本教程旨在保持简单。

前提条件

第一个前提条件是 OpenCV 必须使用并行框架进行构建。在 OpenCV 3.2 中，按以下顺序列出可用的并行框架：

Intel Threading Building Blocks（第三方库，应明确启用）
C= Parallel C/C++ 编程语言扩展（第三方库，应明确启用）
OpenMP (编译器集成，应显式启用)
APPLE GCD (系统范围，自动使用 (仅限 APPLE))
Windows RT 并发（系统范围，自动使用（仅限 Windows RT））
Windows 并发（运行时的一部分，自动使用（仅限 Windows - MSVC++ >= 10））
Pthreads（如果可用）

如您所见，OpenCV 库中可以使用多种并行框架。一些并行库是第三方库，必须在 CMake 中明确构建和启用（例如 TBB、C=），另一些则随平台自动可用（例如 APPLE GCD），但您很可能可以通过直接方式或在 CMake 中启用选项并重新构建库来访问并行框架。

第二个（弱）前提条件与您希望完成的任务更相关，因为并非所有计算都适合/可以适应以并行方式运行。简单来说，可以分解为多个基本操作且没有内存依赖（无可能的竞态条件）的任务很容易并行化。计算机视觉处理通常很容易并行化，因为大多数时候一个像素的处理不依赖于其他像素的状态。

简单示例：绘制曼德布罗集

我们将使用绘制曼德布罗集的例子来展示如何从常规的串行代码轻松地将其改编为并行计算。

理论

曼德布罗集的定义是由数学家 Adrien Douady 为纪念数学家 Benoit Mandelbrot 而命名的。它在数学领域之外也很有名，因为其图像表示是分形（一种在每个尺度上都显示重复模式的数学集合）的一个例子（更重要的是，曼德布罗集是自相似的，因为整个形状可以在不同尺度上重复出现）。有关更深入的介绍，您可以查看相应的维基百科文章。在这里，我们只介绍绘制曼德布罗集的公式（来自上述维基百科文章）。

‍曼德布罗集是复平面中所有 \( c \) 值的集合，对于这些 \( c \) 值，二次映射迭代下 0 的轨道
\[\begin{cases} z_0 = 0 \\ z_{n+1} = z_n^2 + c \end{cases}\]

保持有界。也就是说，如果从 \( z_0 = 0 \) 开始并重复应用迭代，无论 \( n \) 变得多大，\( z_n \) 的绝对值始终保持有界，则复数 \( c \) 是曼德布罗集的一部分。这也可以表示为
\[\limsup_{n\to\infty}|z_{n+1}|\leqslant2\]

伪代码

一种生成曼德布罗集表示的简单算法称为“逃逸时间算法”。对于渲染图像中的每个像素，我们使用递推关系测试在最大迭代次数下复数是否保持有界。不属于曼德布罗集的像素会快速“逃逸”，而我们假设在固定最大迭代次数后像素属于该集合。高迭代次数会生成更详细的图像，但计算时间也会相应增加。我们使用“逃逸”所需的迭代次数来描绘图像中的像素值。

对于屏幕上的每个像素 (Px, Py)，执行：
{
x0 = 像素的缩放 x 坐标（缩放到曼德布罗 X 轴范围 (-2, 1)）
y0 = 像素的缩放 y 坐标（缩放到曼德布罗 Y 轴范围 (-1, 1)）
x = 0.0
y = 0.0
iteration = 0
max_iteration = 1000
while (x*x + y*y < 2*2 AND iteration < max_iteration) {
xtemp = x*x - y*y + x0
y = 2*x*y + y0
x = xtemp
iteration = iteration + 1
  }
color = palette[iteration]
plot(Px, Py, color)
}

为了将伪代码与理论联系起来，我们有：

\( z = x + iy \)
\( z^2 = x^2 + i2xy - y^2 \)
\( c = x_0 + iy_0 \)

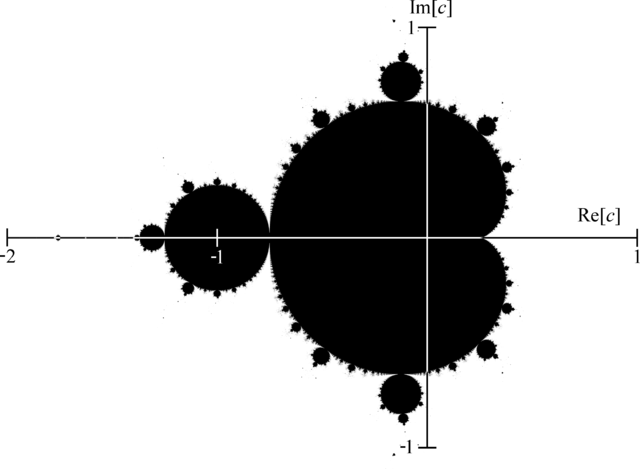
在此图中，我们回顾复数的实部在 x 轴上，虚部在 y 轴上。您可以看到，如果我们放大到特定位置，整个形状可以重复出现。

实现

逃逸时间算法实现

int mandelbrot(const complex<float> &z0, const int max)
{
complex<float> z = z0;
    for (int t = 0; t < max; t++)
    {
        if (z.real()*z.real() + z.imag()*z.imag() > 4.0f) return t;
        z = z*z + z0;
    }
 
    return max;
}

在这里，我们使用了 std::complex 模板类来表示一个复数。此函数执行测试以检查像素是否在集合中，并返回“逃逸”迭代次数。

串行曼德布罗集实现

void sequentialMandelbrot(Mat &img, const float x1, const float y1, const float scaleX, const float scaleY)
{
    for (int i = 0; i < img.rows; i++)
    {
        for (int j = 0; j < img.cols; j++)
        {
            float x0 = j / scaleX + x1;
            float y0 = i / scaleY + y1;
 
complex<float> z0(x0, y0);
            uchar value = (uchar) mandelbrotFormula(z0);
img.ptr<uchar>(i)[j] = value;
        }
    }
}

在此实现中，我们按顺序迭代渲染图像中的像素，以执行测试来检查该像素是否可能属于曼德布罗集。

另一件要做的事情是使用以下方式将像素坐标转换为曼德布罗集空间：

    Mat mandelbrotImg(4800, 5400, CV_8U);
    float x1 = -2.1f, x2 = 0.6f;
    float y1 = -1.2f, y2 = 1.2f;
    float scaleX = mandelbrotImg.cols / (x2 - x1);\
    float scaleY = mandelbrotImg.rows / (y2 - y1);\

最后，为了给像素分配灰度值，我们使用以下规则：

如果像素达到最大迭代次数（假定像素在曼德布罗集中），则该像素为黑色，
否则，我们根据逃逸迭代次数分配一个灰度值，并将其缩放到适合灰度范围。

int mandelbrotFormula(const complex<float> &z0, const int maxIter=500) {
    int value = mandelbrot(z0, maxIter);
    if(maxIter - value == 0)
    {
        return 0;
    }
 
    return cvRound(sqrt(value / (float) maxIter) * 255);
}

使用线性缩放变换不足以感知灰度变化。为了克服这一点，我们将使用平方根缩放变换来增强感知（借鉴自 Jeremy D. Frens 的博客文章）：\( f \left( x \right) = \sqrt{\frac{x}{\text{maxIter}}} \times 255 \)

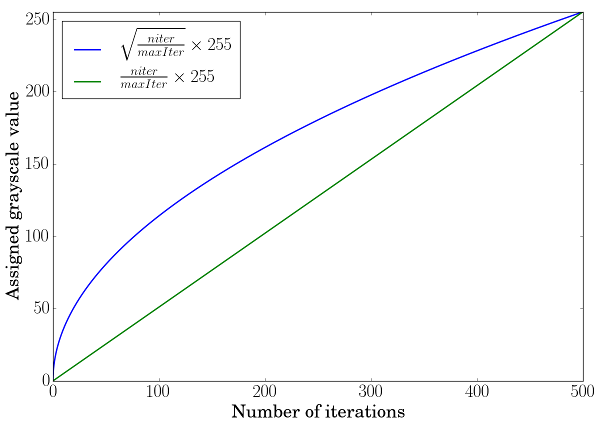
绿色曲线对应于简单的线性缩放变换，蓝色曲线对应于平方根缩放变换，您可以观察到在这些位置查看斜率时，最低值如何得到提升。

并行曼德布罗集实现

查看串行实现时，我们可以注意到每个像素都是独立计算的。为了优化计算，我们可以利用现代处理器的多核架构并行执行多个像素计算。为了轻松实现这一点，我们将使用 OpenCV cv::parallel_for_ 框架。

class ParallelMandelbrot : public ParallelLoopBody
{
public:
ParallelMandelbrot (Mat &img, const float x1, const float y1, const float scaleX, const float scaleY)
: m_img(img), m_x1(x1), m_y1(y1), m_scaleX(scaleX), m_scaleY(scaleY)
    {
    }
 
    virtual void operator ()(const Range& range) const CV_OVERRIDE
    {
        for (int r = range.start; r < range.end; r++)
        {
            int i = r / m_img.cols;
            int j = r % m_img.cols;
 
            float x0 = j / m_scaleX + m_x1;
            float y0 = i / m_scaleY + m_y1;
 
complex<float> z0(x0, y0);
            uchar value = (uchar) mandelbrotFormula(z0);
m_img.ptr<uchar>(i)[j] = value;
        }
    }
 
ParallelMandelbrot& operator=(const ParallelMandelbrot &) {
        return *this;
    };
 
private:
    Mat &m_img;
    float m_x1;
    float m_y1;
    float m_scaleX;
    float m_scaleY;
};

第一件事是声明一个继承自 cv::ParallelLoopBody 的自定义类，并重写 virtual void operator ()(const cv::Range& range) const。

operator () 中的范围表示将由单个线程处理的像素子集。这种分割是自动完成的，以平均分配计算负载。我们必须将像素索引坐标转换为二维 [row, col] 坐标。另请注意，我们必须保留对 Mat 图像的引用，以便能够就地修改图像。

并行执行通过以下方式调用：

ParallelMandelbrot parallelMandelbrot(mandelbrotImg, x1, y1, scaleX, scaleY);

parallel_for_(Range(0, mandelbrotImg.rows*mandelbrotImg.cols), parallelMandelbrot);

在这里，范围表示要执行的操作总数，即图像中的像素总数。要设置线程数，可以使用：cv::setNumThreads。您还可以使用 cv::parallel_for_ 中的 nstripes 参数指定分割数量。例如，如果您的处理器有 4 个线程，设置 cv::setNumThreads(2) 或设置 nstripes=2 应该是一样的，因为默认情况下它将使用所有可用的处理器线程，但只会将工作负载分配给两个线程。

注意: C++ 11 标准允许通过去除 ParallelMandelbrot 类并用 lambda 表达式替换来简化并行实现。

    parallel_for_(Range(0, mandelbrotImg.rows*mandelbrotImg.cols), [&](const Range& range){
for (int r = range.start; r < range.end; r++)
        {
int i = r / mandelbrotImg.cols;
int j = r % mandelbrotImg.cols;
 
float x0 = j / scaleX + x1;
float y0 = i / scaleY + y1;
 
complex<float> z0(x0, y0);
uchar value = (uchar) mandelbrotFormula(z0);
mandelbrotImg.ptr<uchar>(i)[j] = value;
        }
    });

结果

您可以在这里找到完整的教程代码。并行实现的性能取决于您拥有的 CPU 类型。例如，在 4 核 / 8 线程的 CPU 上，您可以预期大约 6.9 倍的加速。有很多因素可以解释为什么我们没有达到接近 8 倍的加速。主要原因应归结于：

创建和管理线程的开销，
并行运行的后台进程，
4 个硬件核心（每个核心有 2 个逻辑线程）与 8 个硬件核心之间的差异。

教程代码生成的最终图像（您可以修改代码以使用更多迭代，并根据逃逸迭代次数分配像素颜色，并使用调色板以获得更美观的图像）：

目录

目标

前提条件

简单示例：绘制曼德布罗集

理论

伪代码

实现

逃逸时间算法实现

串行曼德布罗集实现

并行曼德布罗集实现

结果