结构分析与形状描述符

详细说明

命名空间
命名空间	cv::traits

类
类	cv::GeneralizedHough
	使用广义霍夫变换在灰度图像中找到任意模板 更多...
类	cv::GeneralizedHoughBallard
	使用广义霍夫变换在灰度图像中找到任意模板 更多...
类	cv::GeneralizedHoughGuil
	使用广义霍夫变换在灰度图像中找到任意模板 更多...
类	cv::Moments
	由 cv::moments 返回的结构 更多...

枚举
枚举	cv::ConnectedComponentsAlgorithmsTypes {   cv::CCL_DEFAULT = -1 ,   cv::CCL_WU = 0 ,   cv::CCL_GRANA = 1 ,   cv::CCL_BOLELLI = 2 ,   cv::CCL_SAUF = 3 ,   cv::CCL_BBDT = 4 ,   cv::CCL_SPAGHETTI = 5 }
	连通组件算法 更多...
枚举	cv::ConnectedComponentsTypes {   cv::CC_STAT_LEFT = 0 ,   cv::CC_STAT_TOP = 1 ,   cv::CC_STAT_WIDTH = 2 ,   cv::CC_STAT_HEIGHT = 3 ,   cv::CC_STAT_AREA = 4 }
	连通组件统计 更多...
枚举	cv::ContourApproximationModes {   cv::CHAIN_APPROX_NONE = 1 ,   cv::CHAIN_APPROX_SIMPLE = 2 ,   cv::CHAIN_APPROX_TC89_L1 = 3 ,   cv::CHAIN_APPROX_TC89_KCOS = 4 }
	轮廓近似算法 更多...
枚举	cv::RectanglesIntersectTypes {   cv::INTERSECT_NONE = 0 ,   cv::INTERSECT_PARTIAL = 1 ,   cv::INTERSECT_FULL = 2 }
	矩形之间交型的类型 更多...
枚举	cv::RetrievalModes {   cv::RETR_EXTERNAL = 0 ,   cv::RETR_LIST = 1 ,   cv::RETR_CCOMP = 2 ,   cv::RETR_TREE = 3 ,   cv::RETR_FLOODFILL = 4 }
	轮廓检索算法的模式 更多...
枚举	cv::ShapeMatchModes {   cv::CONTOURS_MATCH_I1 =1 ,   cv::CONTOURS_MATCH_I2 =2 ,   cv::CONTOURS_MATCH_I3 =3 }
	形状匹配方法。 更多...

函数
void	cv::approxPolyDP (InputArray curve, OutputArray approxCurve, double epsilon, bool closed)
	以指定的精度逼近多边形曲线(s)。
double	cv::arcLength (InputArray curve, bool closed)
	计算轮廓周长或曲线长度。
Rect	cv::boundingRect (InputArray array)
	计算点集或灰度图像非零像素的上右上边界矩形。
void	cv::boxPoints (RotatedRect box, OutputArray points)
	找到旋转矩形的四个顶点。用于绘制旋转矩形。
int	cv::connectedComponents (InputArray image, OutputArray labels, int connectivity, int ltype, int ccltype)
	计算布尔图像的连通分量标记图像
int	cv::connectedComponents (InputArray image, OutputArray labels, int connectivity=8, int ltype=CV_32S)
int	cv::connectedComponentsWithStats (InputArray image, OutputArray labels, OutputArray stats, OutputArray centroids, int connectivity, int ltype, int ccltype)
	计算布尔图像的连通分量标记图像，并为每个标记生成统计输出
int	cv::connectedComponentsWithStats (InputArray image, OutputArray labels, OutputArray stats, OutputArray centroids, int connectivity=8, int ltype=CV_32S)
double	cv::contourArea (InputArray contour, bool oriented=false)
	计算轮廓面积。
void	cv::convexHull (InputArray points, OutputArray hull, bool clockwise=false, bool returnPoints=true)
	找到点集的凸包。
void	cv::convexityDefects (InputArray contour, InputArray convexhull, OutputArray convexityDefects)
	找到轮廓的凸缺陷。
Ptr< GeneralizedHoughBallard >	cv::createGeneralizedHoughBallard ()
	创建一个指向 cv::GeneralizedHoughBallard 类的智能指针并将其初始化。
Ptr< GeneralizedHoughGuil >	cv::createGeneralizedHoughGuil ()
	创建一个指向 cv::GeneralizedHoughGuil 类的智能指针并将其初始化。
void	cv::findContours (InputArray image, OutputArrayOfArrays contours, int mode, int method, Point offset=Point())
void	cv::findContours (InputArray image, OutputArrayOfArrays contours, OutputArray hierarchy, int mode, int method, Point offset=Point())
	在二值图像中查找轮廓。
void	cv::findContoursLinkRuns (InputArray image, OutputArrayOfArrays contours)
	这是一个重载的函数成员，提供方便。它与上述函数的不同之处在于它接受的参数。
void	cv::findContoursLinkRuns (InputArray image, OutputArrayOfArrays contours, OutputArray hierarchy)
	使用链跑算法查找轮廓。
RotatedRect	cv::fitEllipse (InputArray points)
	将椭圆拟合到一组2D点。
RotatedRect	cv::fitEllipseAMS (InputArray points)
	将椭圆拟合到一组2D点。
RotatedRect	cv::fitEllipseDirect (InputArray points)
	将椭圆拟合到一组2D点。
void	cv::fitLine (InputArray points, OutputArray line, int distType, double param, double reps, double aeps)
	将线拟合到二维或三维点集。
void	cv::HuMoments (const Moments &m, OutputArray hu)
void	cv::HuMoments (const Moments &moments, double hu[7])
	计算七个Hu不变量。
float	cv::intersectConvexConvex (InputArray p1, InputArray p2, OutputArray p12, bool handleNested=true)
	找到两个凸多边形相交的区域。
bool	cv::isContourConvex (InputArray contour)
	测试轮廓的凸性。
double	cv::matchShapes (InputArray contour1, InputArray contour2, int method, double parameter)
	比较两个形状。
RotatedRect	cv::minAreaRect (InputArray points)
	找到最小面积的包含输入二维点集的旋转矩形。
void	cv::minEnclosingCircle (InputArray points, Point2f &center, float &radius)
	找到包含二维点集的最小面积的圆。
double	cv::minEnclosingTriangle (InputArray points, OutputArray triangle)
	找到包围二维点集的最小面积的三角形，并返回其面积。
Moments	cv::moments (InputArray array, bool binaryImage=false)
	计算多边形或光栅化形状的到三阶的所有矩。
double	cv::pointPolygonTest (InputArray contour, Point2f pt, bool measureDist)
	执行区域内的点测试。
int	cv::rotatedRectangleIntersection (const RotatedRect &rect1, const RotatedRect &rect2, OutputArray intersectingRegion)
	判断两个旋转矩形是否有交集。

枚举类型文档

ConnectedComponentsAlgorithmsTypes

enum cv::ConnectedComponentsAlgorithmsTypes

#include <opencv2/imgproc.hpp>

连接组件算法

枚举值
CCL_DEFAULT  Python: cv.CCL_DEFAULT	8向连通性的Spaghetti算法，4向连通性的Spaghetti4C算法。
CCL_WU  Python: cv.CCL_WU	8向连通性的SAUF算法，4向连通性的SAUF算法。SAUF的并行实现如[30]所述。
CCL GRANA  Python: cv.CCL_GRANA	8向连通性的BBDT算法，4向连通性的SAUF算法。BBDT和SAUF的并行实现如[30]所述。
CCL_BOLELLI  Python: cv.CCL_BOLELLI	8向连通性的Spaghetti算法，4向连通性的Spaghetti4C算法。Spaghetti和Spaghetti4C的并行实现如[30]所述。
CCL_SAUF  Python: cv.CCL_SAUF	与CCL_WU相同。建议使用算法名的标志（CCL_SAUF）而不是第一作者的标志（CCL_WU）。
CCL_BBDT  Python: cv.CCL_BBDT	与CCL_GRANA相同。建议使用算法名的标志（CCL_BBDT）而不是第一作者的标志（CCL_GRANA）。
CCL_SPAGHETTI  Python: cv.CCL_SPAGHETTI	与CCL_BOLELLI相同。建议使用算法名的标志（CCL_SPAGHETTI）而不是第一作者的标志（CCL_BOLELLI）。

ConnectedComponentsTypes

enum cv::ConnectedComponentsTypes

#include <opencv2/imgproc.hpp>

连接组件统计

枚举值
CC_STAT_LEFT  Python: cv.CC_STAT_LEFT	水平方向上包含的边界框的最左（x）坐标。
CC_STAT_TOP  Python: cv.CC_STAT_TOP	垂直方向上包含的边界框的最上（y）坐标。
CC_STAT_WIDTH  Python: cv.CC_STAT_WIDTH	边界框的水平尺寸。
CC_STAT_HEIGHT  Python: cv.CC_STAT_HEIGHT	边界框的垂直尺寸。
CC_STAT_AREA  Python: cv.CC_STAT_AREA	连通组件的总面积（以像素为单位）。

ContourApproximationModes

枚举 cv::ContourApproximationModes

#include <opencv2/imgproc.hpp>

轮廓近似算法

枚举值
CHAIN_APPROX_NONE  Python: cv.CHAIN_APPROX_NONE	存储轮廓的所有点。也就是说，任何两个连续的轮廓点（x1, y1）和（x2, y2）将要么是水平、垂直或对角邻居，即 max(abs(x1 - x2), abs(y2 - y1)) == 1。
CHAIN_APPROX_SIMPLE  Python: cv.CHAIN_APPROX_SIMPLE	压缩水平和垂直以及对角线段，只留下它们的端点。例如，直立矩形轮廓用4个点来编码。
CHAIN_APPROX_TC89_L1  Python: cv.CHAIN_APPROX_TC89_L1	应用 Teh-Chin 连接近似算法的一种变体 [265]
CHAIN_APPROX_TC89_KCOS  Python: cv.CHAIN_APPROX_TC89_KCOS	应用 Teh-Chin 连接近似算法的一种变体 [265]

RectanglesIntersectTypes

枚举 cv::RectanglesIntersectTypes

#include <opencv2/imgproc.hpp>

矩形之间的交点类型

枚举值
INTERSECT_NONE  Python: cv.INTERSECT_NONE	没有交点。
INTERSECT_PARTIAL  Python: cv.INTERSECT_PARTIAL	存在部分交点。
INTERSECT_FULL  Python: cv.INTERSECT_FULL	一个矩形完全包含在另一个矩形内。

RetrievalModes

枚举 cv::RetrievalModes

#include <opencv2/imgproc.hpp>

轮廓检索算法的模式的轮廓。

枚举值
RETR_EXTERNAL  Python: cv.RETR_EXTERNAL	只检索外部轮廓。对于所有轮廓，它设置 hierarchy[i][2]=hierarchy[i][3]=-1。
RETR_LIST  Python: cv.RETR_LIST	检索所有轮廓，但不建立任何层次关系。
RETR_CCOMP  Python: cv.RETR_CCOMP	检索所有轮廓并将它们组织成两层层次结构。在顶层，有组件的外部边界。在第二层，有孔的边界。如果一个连通组件内的孔还有另一个轮廓，它仍然放在顶层。
RETR_TREE  Python: cv.RETR_TREE	检索所有轮廓并重建嵌套轮廓的全层次结构。
RETR_FLOODFILL  Python: cv.RETR_FLOODFILL

ShapeMatchModes

枚举 cv::ShapeMatchModes

#include <opencv2/imgproc.hpp>

形状匹配方法。

（\(A\)表示对象1，\(B\)表示对象2）

$$m^{A}_i = \mathrm{sign}(h^{A}_i) \cdot \log{h^{A}_i} \\

其中 \(h^{A}_i\) 和 \(h^{B}_i\) 分别是 \(A\) 和 \(B\) 的Hu矩。

枚举值
CONTOURS_MATCH_I1  Python: cv.CONTOURS_MATCH_I1	$$I_1(A,B) = \sum_{i=1...7} \left | \frac{1}{m^{A}_i} - \frac{1}{m^{B}_i} \right |$$
CONTOURS_MATCH_I2  Python: cv.CONTOURS_MATCH_I2	$$I_2(A,B) = \sum_{i=1...7} \left | m^{A}_i - m^{B}_i \right |$$
CONTOURS_MATCH_I3  Python: cv.CONTOURS_MATCH_I3	$$I_3(A,B) = \max_{i=1...7} \frac{\left | m^{A}_i - m^{B}_i \right |}{\left | m^{A}_i \right |}$$

函数文档

approxPolyDP()

void cv::approxPolyDP	(	InputArray	curve,
		OutputArray	approxCurve,
		double	epsilon,
		bool	closed
	)

Python
	cv.approxPolyDP(	curve, epsilon, closed[, approxCurve]	) ->	approxCurve

#include <opencv2/imgproc.hpp>

以指定的精度逼近多边形曲线(s)。

函数 cv::approxPolyDP 估算曲线或多边形的精度，通过与其他曲线/多边形进行估算，使得它们之间的距离小于或等于指定的精度。它使用 Douglas-Peucker 算法 http://en.wikipedia.org/wiki/Ramer-Douglas-Peucker_algorithm

参数

curve	2D点的输入向量，存储在 std::vector 或 Mat
approxCurve	估算的结果。其类型应与输入曲线的类型匹配。
epsilon	指定近似的精度。这是原始曲线与其近似值之间的最大距离。
closed	如果为 true，则估算的曲线是封闭的（其第一个和最后一个顶点连接）。否则，它不是封闭的。

arcLength()

double cv::arcLength	(	InputArray	curve,
		bool	closed
	)

Python
	cv.arcLength(	curve, closed	) ->	retval

#include <opencv2/imgproc.hpp>

计算轮廓周长或曲线长度。

该函数计算曲线长度或封闭轮廓的周长。

参数

curve	2D点的输入向量，存储在 std::vector 或 Mat。
closed	表示曲线是否闭合的标志。

boundingRect()

Rect cv::boundingRect

(

InputArray

array

)

Python
	cv.boundingRect(	array	) ->	retval

#include <opencv2/imgproc.hpp>

计算点集或灰度图像非零像素的上右上边界矩形。

函数计算并返回指定点集或灰度图像中非零像素的最小 upright 矩形。

参数

array

灰度图像或 2D 点集的输入，存储在 std::vector 或 Mat。

boxPoints()

void cv::boxPoints	(	RotatedRect	box,
		OutputArray	points
	)

Python
	cv.boxPoints(	box[, points]	) ->	points

#include <opencv2/imgproc.hpp>

找到旋转矩形的四个顶点。用于绘制旋转矩形。

该函数查找旋转矩形的四个顶点。此函数对绘制矩形非常有用。在 C++ 中，除使用此函数外，还可以直接使用 RotatedRect::points 方法。更多有关创建轮廓的边界旋转框和椭圆的教程，请参阅 Creating Bounding rotated boxes and ellipses for contours。

参数

box	输入旋转矩形。可能是由 minAreaRect 生成的输出。
points	矩形四顶点的输出数组。

connectedComponents() [1/2]

int cv::connectedComponents	(	InputArray	image,
		OutputArray	labels,
		int	connectivity,
		int	ltype,
		int	ccltype
	)

Python
	cv.connectedComponents(	image[, labels[, connectivity[, ltype]]]	) ->	retval, labels
	cv.connectedComponentsWithAlgorithm(	image, connectivity, ltype, ccltype[, labels]	) ->	retval, labels

#include <opencv2/imgproc.hpp>

计算布尔图像的连通分量标记图像

图像具有4或8向连通性 - 返回N，代表标签的总数[0, N-1]，其中0表示背景标签。ltype指定输出标签图像类型，这是基于标签总数或源图像中像素总数的一个重要的考虑因素。ccltype指定使用的连通组件标签算法，目前支持Bolelli (Spaghetti) [31]，Grana (BBDT) [110]和Wu的(SAUФ) [300]算法，详细信息请参看连通组件算法类型。注意，SAUF算法强制对标签进行行优先排序，而Spaghetti和BBDT没有这样做。如果启用了至少一个允许的并行框架，且图像的行至少是getNumberOfCPUs 返回值的两倍，则此函数将使用算法的并行版本（包括统计数据）。

参数

image	待标记的8位单通道图像
labels	目标标记图像
connectivity	分别表示8路或4路连通性的8或4
ltype	输出图像标签类型。目前支持CV_32S和CV_16U
ccltype	连通组件算法类型（请参阅连通组件算法类型）。

connectedComponents() [2/2]

int cv::connectedComponents	(	InputArray	image,
		OutputArray	labels,
		int	connectivity = 8,
		int	ltype = CV_32S
	)

Python
	cv.connectedComponents(	image[, labels[, connectivity[, ltype]]]	) ->	retval, labels
	cv.connectedComponentsWithAlgorithm(	image, connectivity, ltype, ccltype[, labels]	) ->	retval, labels

#include <opencv2/imgproc.hpp>

这是一个重载的函数成员，提供方便。它与上述函数的不同之处在于它接受的参数。

参数

image	待标记的8位单通道图像
labels	目标标记图像
connectivity	分别表示8路或4路连通性的8或4
ltype	输出图像标签类型。目前支持CV_32S和CV_16U

connectedComponentsWithStats() [1/2]

int cv::connectedComponentsWithStats	(	InputArray	image,
		OutputArray	labels,
		OutputArray	stats,
		OutputArray	centroids,
		int	connectivity,
		int	ltype,
		int	ccltype
	)

Python
	cv.connectedComponentsWithStats(	image[, labels[, stats[, centroids[, connectivity[, ltype]]]]]	) ->	retval, labels, stats, centroids
	cv.connectedComponentsWithStatsWithAlgorithm(	image, connectivity, ltype, ccltype[, labels[, stats[, centroids]]]	) ->	retval, labels, stats, centroids

#include <opencv2/imgproc.hpp>

计算布尔图像的连通分量标记图像，并为每个标记生成统计输出

图像具有4或8向连通性 - 返回N，代表标签的总数[0, N-1]，其中0表示背景标签。ltype指定输出标签图像类型，这是基于标签总数或源图像中像素总数的一个重要的考虑因素。ccltype指定使用的连通组件标签算法，目前支持Bolelli (Spaghetti) [31]，Grana (BBDT) [110]和Wu的(SAUФ) [300]算法，详细信息请参看连通组件算法类型。注意，SAUF算法强制对标签进行行优先排序，而Spaghetti和BBDT没有这样做。如果启用了至少一个允许的并行框架，且图像的行至少是getNumberOfCPUs 返回值的两倍，则此函数将使用算法的并行版本（包括统计数据）。

参数

image	待标记的8位单通道图像
labels	目标标记图像
stats	每个标签的统计数据输出，包括背景标签。统计数据通过stats(label, COLUMN)访问，其中COLUMN是连通组件类型之一，选择统计项。数据类型是CV_32S。
centroids	每个标签的重心输出，包括背景标签。重心的访问方式为 centroids(label, 0) 用于 x 轴，centroids(label, 1) 用于 y 轴。数据类型为 CV_64F。
connectivity	分别表示8路或4路连通性的8或4
ltype	输出图像标签类型。目前支持CV_32S和CV_16U
ccltype	连通组件算法类型（见 连通组件算法类型）。

connectedComponentsWithStats() [2/2]

int cv::connectedComponentsWithStats	(	InputArray	image,
		OutputArray	labels,
		OutputArray	stats,
		OutputArray	centroids,
		int	connectivity = 8,
		int	ltype = CV_32S
	)

Python
	cv.connectedComponentsWithStats(	image[, labels[, stats[, centroids[, connectivity[, ltype]]]]]	) ->	retval, labels, stats, centroids
	cv.connectedComponentsWithStatsWithAlgorithm(	image, connectivity, ltype, ccltype[, labels[, stats[, centroids]]]	) ->	retval, labels, stats, centroids

#include <opencv2/imgproc.hpp>

这是一个重载的函数成员，提供方便。它与上述函数的不同之处在于它接受的参数。

参数

image	待标记的8位单通道图像
labels	目标标记图像
stats	每个标签的统计数据输出，包括背景标签。统计数据通过stats(label, COLUMN)访问，其中COLUMN是连通组件类型之一，选择统计项。数据类型是CV_32S。
centroids	每个标签的重心输出，包括背景标签。重心的访问方式为 centroids(label, 0) 用于 x 轴，centroids(label, 1) 用于 y 轴。数据类型为 CV_64F。
connectivity	分别表示8路或4路连通性的8或4
ltype	输出图像标签类型。目前支持CV_32S和CV_16U

contourArea()

double cv::contourArea	(	InputArray	contour,
		bool	面向 = false
	)

Python
	cv.contourArea(	contour[, oriented]	) ->	retval

#include <opencv2/imgproc.hpp>

计算轮廓面积。

此函数计算轮廓面积。类似于矩，面积使用格林公式计算。因此，使用 drawContours 或 fillPoly 绘制轮廓时，返回的面积和零像素数量可能会有所不同。函数对于有自相交的轮廓很可能给出错误的结果。

示例

vector<Point> contour;
contour.push_back(Point2f(0, 0));
contour.push_back(Point2f(10, 0));
contour.push_back(Point2f(10, 10));
contour.push_back(Point2f(5, 4));
 
double area0 = contourArea(contour);
vector<Point> approx;
approxPolyDP(contour, approx, 5, true);
double area1 = contourArea(approx);
 
cout << "area0 =" << area0 << endl <<
        "area1 =" << area1 << endl <<
        "approx poly vertices" << approx.size() << endl;

参数

contour	输入向量 2D 点（轮廓顶点），存储在 std::vector 或 Mat 中。
oriented	面向区域标志。如果为 true，函数返回一个带符号的区域值，取决于轮廓的方向（顺时针或逆时针）。使用此功能可以通过取区域值的符号来确定轮廓的方向。默认情况下，参数为 false，表示返回绝对值。

convexHull()

void cv::convexHull	(	InputArray	points,
		OutputArray	hull,
		bool	顺时针 = false,
		bool	返回点 = true
	)

Python
	cv.convexHull(	points[, hull[, clockwise[, returnPoints]]]	) ->	hull

#include <opencv2/imgproc.hpp>

找到点集的凸包。

函数 cv::convexHull 使用 Sklansky 算法 [246] 寻找一个 2D 点集的凸包，该算法的当前实现中具有 O(N logN) 复杂性。

参数

points	2D 点集输入，存储在 std::vector 或 Mat 中。
hull	输出凸包。它可以是一个整数索引向量或点向量。在第一种情况下，凸包元素是原数组的凸包点（因为凸包点的集合是原点集的子集）的0起始索引。在第二种情况下，凸包元素是凸包点本身。
顺时针	方向标志。如果是true，则输出的凸包是顺时针方向的。否则，它是对抗方向的。默认的坐标系中，X轴指向右侧，Y轴向上。
returnPoints	操作标志。在矩阵的情况下，当此标志为true时，函数返回凸包点。否则，返回凸包点的索引。当输出数组是std::vector时，此标志被忽略，输出取决于向量的类型：std::vector表示returnPoints=false，std::vector表示returnPoints=true。

备注

points和hull应该是不同的数组，不支持原地处理。

有关更多详情，请参阅相应的教程[258]。

有用链接

https://www.learnopencv.com/convex-hull-using-opencv-in-python-and-c/

convexityDefects()

void cv::convexityDefects	(	InputArray	contour,
		InputArray	convexhull,
		OutputArray	convexityDefects
	)

Python
	cv.convexityDefects(	contour, convexhull[, convexityDefects]	) ->	convexityDefects

#include <opencv2/imgproc.hpp>

找到轮廓的凸缺陷。

以下图显示了手部轮廓的凸性缺陷

image

参数

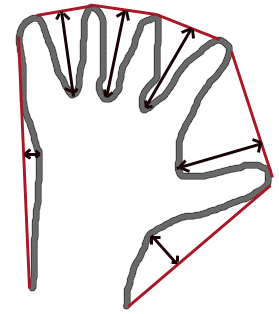
contour	输入轮廓。
convexhull	使用convexHull得到的凸包，其中应包含构成凸包的轮廓点索引。
convexityDefects	凸性缺陷输出向量。在C++和新的Python/Java接口中，每个凸性缺陷表示为4个元素的整数向量（称为Vec4i）：(开始索引，结束索引，最远点索引，固定点深度)，其中索引是原始轮廓中凸性缺陷开始、结束和最远点的0起始索引，固定点深度是固定点逼近（具有8个分数位）的最远轮廓点与凸包之间的距离。也就是说，要获取深度值的浮点数将是fixpt_depth/256.0。

createGeneralizedHoughBallard()

Ptr< GeneralizedHoughBallard > cv::createGeneralizedHoughBallard

(

)

Python
	cv.createGeneralizedHoughBallard(		) ->	retval

#include <opencv2/imgproc.hpp>

创建一个指向 cv::GeneralizedHoughBallard 类的智能指针并将其初始化。

createGeneralizedHoughGuil()

Ptr< GeneralizedHoughGuil > cv::createGeneralizedHoughGuil

(

)

Python
	cv.createGeneralizedHoughGuil(		) ->	retval

#include <opencv2/imgproc.hpp>

创建一个指向 cv::GeneralizedHoughGuil 类的智能指针并将其初始化。

findContours() [1/2]

void cv::findContours	(	InputArray	image,
		OutputArrayOfArrays	contours,
		int	mode,
		int	method,
		Point	offset = Point()
	)

Python
	cv.findContours(	image, mode, method[, contours[, hierarchy[, offset]]]	) ->	contours, hierarchy

#include <opencv2/imgproc.hpp>

这是一个重载的函数成员，提供方便。它与上述函数的不同之处在于它接受的参数。

findContours() [2/2]

void cv::findContours	(	InputArray	image,
		OutputArrayOfArrays	contours,
		OutputArray	hierarchy,
		int	mode,
		int	method,
		Point	offset = Point()
	)

Python
	cv.findContours(	image, mode, method[, contours[, hierarchy[, offset]]]	) ->	contours, hierarchy

#include <opencv2/imgproc.hpp>

在二值图像中查找轮廓。

此函数使用算法[259]从二值图像中检索轮廓。轮廓是形状分析和对象检测与识别的有用工具。请参阅Opencv样本目录中的squares.cpp。

备注

从Opencv 3.2开始，源图像不会被此函数修改。

参数

image	源图像，一个8位单通道图像。非零像素视为1，零像素保留为0，因此图像被视为二进制。您可以使用compare、inRange、threshold、adaptiveThreshold、Canny和其他方法将灰度或彩色图像转换为二进制图像。如果模式等于RETR_CCOMP或RETR_FLOODFILL，输入也可以是32位整数图像的标签（CV_32SC1）。
contours	检测到的轮廓。每个轮廓存储为一个点的向量（例如std::vector>）。
hierarchy	可选输出向量（例如std::vector），包含关于图像拓扑的信息。它的元素数量与轮廓数量相同。对于第i个轮廓contours[i]，元素hierarchy[i][0]、hierarchy[i][1]、hierarchy[i][2]和hierarchy[i][3]设置为同一个层次中下一个和前一个轮廓的索引（从0开始），分别是第一个子轮廓和父轮廓。如果对于轮廓i没有下一个、前一个、父轮廓或嵌套轮廓，则hierarchy[i]中相应的元素将是负数。

备注

在Python中，hierarchy嵌套在顶级数组中。使用hierarchy[0][i]来访问第i个轮廓的层次结构元素。

参数

mode	轮廓检索模式，见RetrievalModes
method	轮廓逼近方法，见ContourApproximationModes
偏移量	可选偏移量，每个轮廓点将根据此偏移量位移。如果轮廓是从图像ROI中提取的，并且需要在整个图像上下文中分析它们，这很有用。

findContoursLinkRuns() [1/2]

void cv::findContoursLinkRuns	(	InputArray	image,
		OutputArrayOfArrays	contours
	)

Python
	cv.findContoursLinkRuns(	image[, contours[, hierarchy]]	) ->	contours, hierarchy
	cv.findContoursLinkRuns(	image[, contours]	) ->	contours

#include <opencv2/imgproc.hpp>

这是一个重载的函数成员，提供方便。它与上述函数的不同之处在于它接受的参数。

findContoursLinkRuns() [2/2]

void cv::findContoursLinkRuns	(	InputArray	image,
		OutputArrayOfArrays	contours,
		OutputArray	hierarchy
	)

Python
	cv.findContoursLinkRuns(	image[, contours[, hierarchy]]	) ->	contours, hierarchy
	cv.findContoursLinkRuns(	image[, contours]	) ->	contours

#include <opencv2/imgproc.hpp>

使用链跑算法查找轮廓。

此函数实现了一个不同于cv::findContours的算法

• 不内部分配临时图像，因此它具有较低的内存消耗
• 仅支持CV_8UC1图像
• 仅输出2级层次结构（RETR_CCOMP模式）
• 不支持除CHAIN_APPROX_SIMPLE之外的其他逼近变化。在其他所有方面，此函数与cv::findContours兼容。

fitEllipse()

RotatedRect cv::fitEllipse

(

InputArray

points

)

Python
	cv.fitEllipse(	points	) ->	retval

#include <opencv2/imgproc.hpp>

将椭圆拟合到一组2D点。

该函数计算能最好地（采用最小二乘法）拟合一组2D点的椭圆。它返回包含椭圆的旋转矩形。使用的是由[92]描述的第一个算法。开发者应注意到，返回的椭圆/旋转矩形数据可能包含负索引，因为数据点接近包含Mat元素的边界。

参数

points

输入2D点集，存储在std::vector<>或Mat中

fitEllipseAMS()

RotatedRect cv::fitEllipseAMS

(

InputArray

points

)

Python
	cv.fitEllipseAMS(	points	) ->	retval

#include <opencv2/imgproc.hpp>

将椭圆拟合到一组2D点。

该函数计算一组2D点的椭圆。它返回包含椭圆的旋转矩形。使用[264]提出的近似均方（AMS）方法。

对于一个椭圆，这个基函数集是 \( \chi= \left(x^2, x y, y^2, x, y, 1\right) \)，这是一组六个自由系数 \( A^T=\left\{A_{\text{xx}},A_{\text{xy}},A_{\text{yy}},A_x,A_y,A_0\right\} \)。然而，要指定一个椭圆，所需的所有东西只是五个数字；主轴和短轴长度 \( (a,b) \)，位置 \( (x_0,y_0) \)，和方向 \( \theta \)。这是因为基函数集包括线，二次，抛物线和双曲函数，以及作为可能拟合的椭圆函数。如果拟合发现是抛物线或双曲线函数，则使用标准的fitEllipse方法。AMS方法通过设定条件 \( A^T ( D_x^T D_x + D_y^T D_y) A = 1 \) 来限制拟合为抛物线，双曲线和椭圆曲线，其中 \( Dx \) 和 \( Dy \) 是设计矩阵 \( D \) 对 x 和 y 的偏导数矩阵。矩阵是逐行形成的，对集合中的每个点应用以下操作

\begin{align*} D(i,:)&=\left\{x_i^2, x_i y_i, y_i^2, x_i, y_i, 1\right\} & D_x(i,:)&=\left\{2 x_i,y_i,0,1,0,0\right\} & D_y(i,:)&=\left\{0,x_i,2 y_i,0,1,0\right\} \end{align*}

AMS方法最小化了成本函数

\begin{equation*} \epsilon ^2=\frac{ A^T D^T D A }{ A^T (D_x^T D_x + D_y^T D_y) A^T } \end{equation*}

通过求解广义特征值问题找到最小成本。

\begin{equation*} D^T D A = \lambda \left( D_x^T D_x + D_y^T D_y\right) A \end{equation*}

参数

points

输入2D点集，存储在std::vector<>或Mat中

fitEllipseDirect()

RotatedRect cv::fitEllipseDirect

(

InputArray

points

)

Python
	cv.fitEllipseDirect(	points	) ->	retval

#include <opencv2/imgproc.hpp>

将椭圆拟合到一组2D点。

该函数计算一组2D点的椭圆。它返回包含椭圆的旋转矩形。使用[93]提出的直接最小二乘法（Direct）。

对于一个椭圆，这个基函数集是 \( \chi= \left(x^2, x y, y^2, x, y, 1\right) \)，这是一组六个自由系数 \( A^T=\left\{A_{\text{xx}},A_{\text{xy}},A_{\text{yy}},A_x,A_y,A_0\right\} \)。然而，要指定一个椭圆，所需的所有东西只是五个数字；主轴和短轴长度 \( (a,b) \)，位置 \( (x_0,y_0) \)，和方向 \( \theta \)。这是因为基函数集包括线，二次，抛物线和双曲函数，以及作为可能拟合的椭圆函数。Direct方法通过确保 \( 4 A_{xx} A_{yy}- A_{xy}^2 > 0 \) 来限制拟合为椭圆。设定的条件是 \( 4 A_{xx} A_{yy}- A_{xy}^2=1 \) 满足不等式，并且由于系数可以任意缩放，所以不会过于严格。

方程式如下：\(\epsilon^2 = A^T D^T D A\)，其中 \(A^T C A =1\)，\(C=\begin{matrix} 0 & 0 & 2 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 & 0 & 0 \\ 2 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}\)

通过求解广义特征值问题找到最小成本。

方程式如下：\(D^T D A = \lambda (C) A\)

系统仅产生一个正特征值 \(\lambda\)，选择与其特征向量 \(\mathbf{u}\) 相关的解。这些结果用于找到系数

方程式如下：\(A = \sqrt{\frac{1}{\mathbf{u}^T C \mathbf{u}}} \mathbf{u}\)

比例因子保证 \(A^T C A =1\)

参数

points

输入2D点集，存储在std::vector<>或Mat中

fitLine()

void cv::fitLine	(	InputArray	points,
		OutputArray	line,
		int	distType,
		double	param,
		double	reps,
		double	aeps
	)

Python
	cv.fitLine(	points, distType, param, reps, aeps[, line]	) ->	line

#include <opencv2/imgproc.hpp>

将线拟合到二维或三维点集。

函数 fitLine 通过最小化 \(\sum_i \rho(r_i)\)，其中 \(r_i\) 是 \(i^{th}\) 点到直线和 \(\rho(r)\) 的距离函数之间的距离，\(\rho(r)\) 是以下几种距离函数之一：

• DIST_L2

  \[\rho (r) = r^2/2 \quad \text{(最简单且最快的最小二乘法)}\]

• DIST_L1

  \[\rho (r) = r\]

• DIST_L12

  \[\rho (r) = 2 \cdot ( \sqrt{1 + \frac{r^2}{2}} - 1)\]

• DIST_FAIR

  \[\rho \left (r \right ) = C^2 \cdot \left ( \frac{r}{C} - \log{\left(1 + \frac{r}{C}\right)} \right ) \quad \text{where} \quad C=1.3998\]

• DIST_WELSCH

  \[\rho \left (r \right ) = \frac{C^2}{2} \cdot \left ( 1 - \exp{\left(-\left(\frac{r}{C}\right)^2\right)} \right ) \quad \text{where} \quad C=2.9846\]

• DIST_HUBER

  \[\rho (r) = \fork{r^2/2}{if \(r < C\)}{C \cdot (r-C/2)}{otherwise} \quad \text{where} \quad C=1.345\]

该算法基于 M-估计器（http://en.wikipedia.org/wiki/M-estimator）技术，通过迭代使用加权最小二乘法拟合直线。每次迭代后，权重 \(w_i\) 都会调整为与 \(\rho(r_i)\) 成反比。

参数

points	2D 或 3D 点的输入向量，存储在 std::vector<> 或 Mat 中。
line	输出直线参数。在 2D 配准时，应该是包含 4 个元素的向量（如 Vec4f）- (vx, vy, x0, y0)，其中 (vx, vy) 是与直线平行的归一化向量，而 (x0, y0) 是直线上的一个点。在 3D 配准时，应该是包含 6 个元素的向量（如 Vec6f）- (vx, vy, vz, x0, y0, z0)，其中 (vx, vy, vz) 是与直线平行的归一化向量，而 (x0, y0, z0) 是直线上的一个点。
distType	M-估计器使用的距离。请参阅DistanceTypes。
param	某些距离类型的数值参数（C）。如果它为 0，则选择最优值。
reps	半径（坐标原点到直线的距离）的足够精度。
aeps	角度的足够精度。0.01 对于 reps 和 aeps 是一个好的默认值。

HuMoments() [1/2]

void cv::HuMoments	(	const Moments &	m,
		OutputArray	hu
	)

Python
	cv.HuMoments(	m[, hu]	) ->	hu

#include <opencv2/imgproc.hpp>

这是一个重载的函数成员，提供方便。它与上述函数的不同之处在于它接受的参数。

HuMoments() [2/2]

void cv::HuMoments	(	const Moments &	moments,
		double	hu[7]
	)

Python
	cv.HuMoments(	m[, hu]	) ->	hu

#include <opencv2/imgproc.hpp>

计算七个Hu不变量。

该函数计算七个 Hu 不变式（在 [131] 中介绍；也请参阅 http://en.wikipedia.org/wiki/Image_moment），定义为：

以下表示Hu不变量的计算：

\(\eta_{ji}\)表示\(\texttt{Moments::nu}_{ji}\)。

这些值被证明是图像尺度、旋转和反射的不变量，除了第七个值，它的符号在反射时改变。这一不变性是以无限图像分辨率的假设作为前提被证明的。在光栅图像的情况下，原始图像和变换图像计算得到的Hu不变量略有不同。

参数

moments	使用moments计算输入矩。
hu	输出Hu不变量。

请参见：

matchShapes

intersectConvexConvex()

float cv::intersectConvexConvex	(	InputArray	p1,
		InputArray	p2,
		OutputArray	p12,
		bool	handleNested = true
	)

Python
	cv.intersectConvexConvex(	p1, p2[, p12[, handleNested]]	) ->	retval, p12

#include <opencv2/imgproc.hpp>

找到两个凸多边形相交的区域。

参数

p1	第一个多边形
p2	第二个多边形
p12	输出描述交叉区域的多边形
handleNested	当为true时，如果一个多边形完全包含在另一个多边形内，则找到交集。当为false时，不找到交集。如果多边形共享一条边或一个多边形的顶点位于另一条边的边上，则不认为是嵌套的，且不管handleNested的值如何，总会找到交集。

返回值

交叉多边形面积的绝对值

备注

intersectConvexConvex不确认两个多边形都是凸多边形，如果它们不是凸多边形，将返回无效结果。

isContourConvex()

bool cv::isContourConvex

(

InputArray

contour

)

Python
	cv.isContourConvex(	contour	) ->	retval

#include <opencv2/imgproc.hpp>

测试轮廓的凸性。

该函数测试输入轮廓是否为凸多边形。轮廓必须是简单的，即没有自交。否则，函数的输出是未定义的。

参数

contour

输入2D点的向量，存储在std::vector<>或Mat中

matchShapes()

double cv::matchShapes	(	InputArray	contour1,
		InputArray	contour2,
		int	method,
		double	parameter
	)

Python
	cv.matchShapes(	contour1, contour2, method, parameter	) ->	retval

#include <opencv2/imgproc.hpp>

比较两个形状。

该函数比较两个形状。所有三种实现的方法都使用Hu不变量（参见HuMoments）

参数

contour1	第一个轮廓或灰度图像。
contour2	第二个轮廓或灰度图像。
method	比较方法，参见ShapeMatchModes）
parameter	方法特定的参数（目前不支持）。

minAreaRect()

RotatedRect cv::minAreaRect

(

InputArray

points

)

Python
	cv.minAreaRect(	points	) ->	retval

#include <opencv2/imgproc.hpp>

找到最小面积的包含输入二维点集的旋转矩形。

该函数计算并返回指定点集的最小面积边界矩形（可能旋转）。开发人员应记住，当数据接近包含Mat元素边界时，返回的RotatedRect可以包含负索引。

参数

points

输入2D点的向量，存储在std::vector<>或Mat中

minEnclosingCircle()

void cv::minEnclosingCircle	(	InputArray	points,
		Point2f &	中心,
		float &	半径
	)

Python
	cv.minEnclosingCircle(	points	) ->	中心, 半径

#include <opencv2/imgproc.hpp>

找到包含二维点集的最小面积的圆。

该函数使用迭代算法找到二维点集的最小包围圆。

参数

points	输入2D点的向量，存储在std::vector<>或Mat中
中心	输出圆的中心。
半径	输出圆的半径。

minEnclosingTriangle()

double cv::minEnclosingTriangle	(	InputArray	points,
		OutputArray	三角形
	)

Python
	cv.minEnclosingTriangle(	points[, triangle]	) ->	retval, triangle

#include <opencv2/imgproc.hpp>

找到包围二维点集的最小面积的三角形，并返回其面积。

该函数找到包围给定二维点集的最小面积三角形并返回其面积。下面的图像显示了给定二维点集的输出。二维点用红色*表示，包围的三角形用黄色表示。

最小包围三角形函数的示例输出

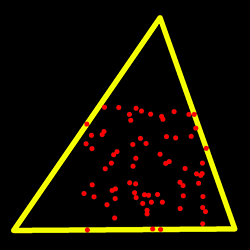
算法的实现基于O'Rourke的[210]和Klee及Laskowski的[148]论文。O'Rourke提供了一个寻找具有n个顶点的二维凸多边形的最小包围三角形的\(\theta(n)\)算法。由于minEnclosingTriangle函数接受二维点集作为输入，因此需要额外的预处理步骤来计算二维点集的凸包。凸包函数的复杂度为\(O(n log(n))\)，这高于\(\theta(n)\)。因此，函数的整体复杂度为\(O(n log(n))\)。

参数

points	具有深度CV_32S或CV_32F的二维点输入向量，存储在std::vector<>中或Mat
三角形	输出由三个二维点定义的三角形顶点的向量。输出数组的深度必须是CV_32F。

moments()

Moments cv::moments	(	InputArray	array,
		bool	binaryImage = false
	)

Python
	cv.moments(	array[, binaryImage]	) ->	retval

#include <opencv2/imgproc.hpp>

计算多边形或光栅化形状的到三阶的所有矩。

该函数计算向量形状或光栅形状的矩，最高到三级。结果返回在结构cv::Moments中。

参数

array	单通道光栅图像（CV_8U，CV_16U，CV_16S，CV_32F，CV_64F）或一个二维点数组（Point或Point2f）（ \(1 \times N\) 或 \(N \times 1\) ）。
binaryImage	如果是true，所有非零图像像素都被视为1。此参数仅用于图像。

返回值

moments.

备注

仅适用于Python绑定中的轮廓矩计算：请注意，输入数组应使用np.int32或np.float32类型的numpy。

请参见：

contourArea，arcLength

pointPolygonTest()

double cv::pointPolygonTest	(	InputArray	contour,
		Point2f	pt,
		bool	measureDist
	)

Python
	cv.pointPolygonTest(	contour, pt, measureDist	) ->	retval

#include <opencv2/imgproc.hpp>

执行区域内的点测试。

该函数确定点是否在轮廓内部、外部或位于边（或与顶点重合）。相应地返回正（内部）、负（外部）或零（在边上）的值。当measureDist=false时，返回值分别为+1、-1和0。否则，返回值是点到最近轮廓边的有符号距离。

以下是对函数输出的示例，其中每个图像像素都与轮廓进行了测试。

示例输出

参数

contour	输入轮廓。
pt	测试的点与轮廓。
measureDist	如果为真，函数估计点到最近轮廓边缘的签名距离。否则，函数只检查点是否在轮廓内。

rotatedRectangleIntersection()

int cv::rotatedRectangleIntersection	(	const RotatedRect &	rect1,
		const RotatedRect &	rect2,
		OutputArray	intersectingRegion
	)

Python
	cv.rotatedRectangleIntersection(	rect1, rect2[, intersectingRegion]	) ->	retval, intersectingRegion

#include <opencv2/imgproc.hpp>

判断两个旋转矩形是否有交集。

如果存在，则返回相交区域的顶点。

以下是一些相交配置的示例。阴影图案表示相交区域，红色顶点是函数返回的。

相交示例

参数

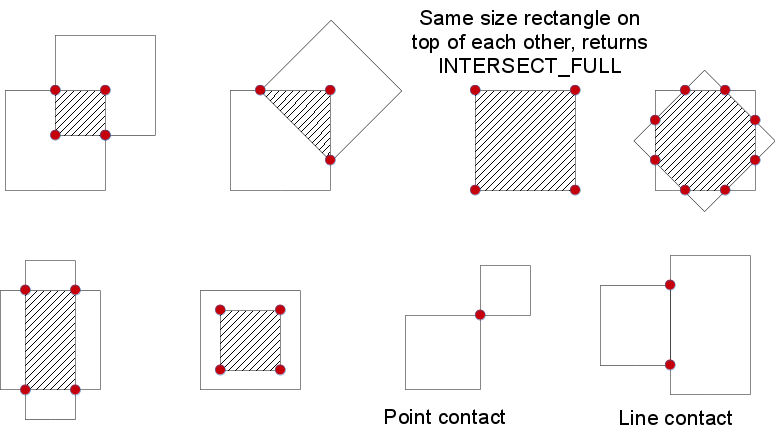
rect1	第一个矩形
rect2	第二个矩形
intersectingRegion	相交区域顶点的输出数组。最多返回8个顶点，存储为 std::vector<cv::Point2f> 或 cv::Mat，类型为 Mx1 CV_32FC2。

返回值

之一 RectanglesIntersectTypes