使用代码讲解单应的基本概念

目录

• 简介
  • 基本理论
    • 什么是单应矩阵？
    • 单应变换有何用处？
  • 演示代码
    • 演示 1：从共面点估计位姿
    • 演示 2：透视校正
    • 演示 3：摄像机位移导致的单应
      • 练习题
    • 演示 4：分解单应矩阵
    • 演示 5：从旋转摄像机中进行基本全景拼接
  • 其他参考内容

上一教程： AKAZE 和 ORB 平面跟踪

兼容性	OpenCV >= 3.0

简介

本文将通过一些代码演示单应的基本概念。有关理论的详细说明，请参考计算机视觉课程或计算机视觉书籍，例如：

• Richard Hartley 和 Andrew Zisserman 编著的《计算机视觉中的多视角几何》，[117]（一些样章可 在此找到，CVPR 教程可 在此找到）
• Yi Ma、Stefano Soatto、Jana Kosecka 和 S. Shankar Sastry 编著的《通往三维视觉的邀请：从图像到几何模型》，[177]（一本计算机视觉书籍手册可 在此找到）
• Richard Szeliski 编著的《计算机视觉：算法与应用》，[259]（一本电子版本可 在此找到）
• Ezio Malis 和 Manuel Vargas 编著的《基于视觉的控制的单应分解的深入理解》，[180]（开放访问，在此）
• Eric Marchand、Hideaki Uchiyama 和 Fabien Spindler 编著的《增强现实的位姿估计：一项实践调查》，[182]（开放访问，在此）

教程代码可在此处找到 C++、Python、Java。本教程中使用的图像可 在此找到（left*.jpg）。

基本理论

什么是单应矩阵？

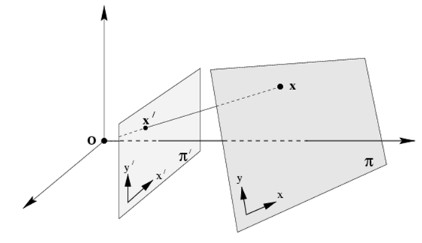
简而言之，平面单应涉及两个平面之间的变换（精确到一个比例因子）

\[ s \begin{bmatrix} x^{'} \\ y^{'} \\ 1 \end{bmatrix} = \mathbf{H} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \]

单应性矩阵是一个3x3矩阵，但它有 8 个自由度 (DoF)，因为它可以估计到一定的规模。它通常被归一化（请参阅 1），其中 \( h_{33} = 1 \) 或 \( h_{11}^2 + h_{12}^2 + h_{13}^2 + h_{21}^2 + h_{22}^2 + h_{23}^2 + h_{31}^2 + h_{32}^2 + h_{33}^2 = 1 \)。

以下示例展示了不同类型的变换，但它们都涉及两个平面之间的变换。

• 平面表面和图像平面（图像摘自 2）

• 两个相机位置观看的平面表面（图像摘自 3和2）

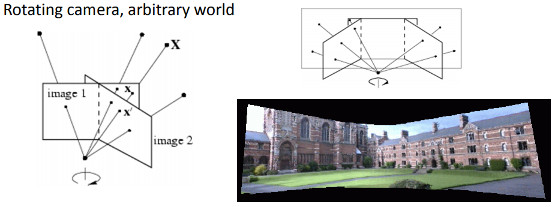
• 旋转相机围绕其投影轴，相当于认为点在无穷远平面（图像摘自 2）

单应性变换如何有用？

• 对于标记增强现实，从共面点估计相机姿态，例如（请参阅前面第一个示例）

• 透视移除 / 校正（请参阅前面第二个示例）

• 全景拼接（请参阅前面第二个和第三个示例）

演示代码

演示 1：从共面点估计姿态

注意

请注意，用于从单应性估计相机姿态的代码是一个示例，如果你想为平面或任意物体估计相机姿态，你应该改为使用 cv::solvePnP。

可以使用直接线性变换 (DLT) 算法来估计单应性（有关更多信息，请参阅 1）。由于物体是平面的，因此用物体坐标系表示的点与用归一化相机坐标系表示的投影到图像平面的点的变换是一个单应性。仅仅因为物体是平面的，所以可以使用单应性来检索相机姿态，假设已知相机内参（请参阅 2 或 4）。可以使用棋盘格物体和 findChessboardCorners() 来轻松地测试这一点，以获取图像中的角点位置。

第一件事是检测棋盘格的角点，此处需要棋盘格大小（patternSize），此处为9x6

vector<Point2f> corners;
    bool found = findChessboardCorners(img, patternSize, corners);

可以根据棋盘方格的尺寸轻松计算在目标框架中表示的目标点位置

        for( int i = 0; i < boardSize.height; i++ )
            for( int j = 0; j < boardSize.width; j++ )
corners.push_back(Point3f(float(j*squareSize),
                                          float(i*squareSize), 0));

计算单应性时必须删除坐标 Z=0

vector<Point3f> objectPoints;
calcChessboardCorners(patternSize, squareSize, objectPoints);
vector<Point2f> objectPointsPlanar;
    for (size_t i = 0; i < objectPoints.size(); i++)
    {
objectPointsPlanar.push_back(Point2f(objectPoints[i].x, objectPoints[i].y));
    }

根据角点并通过应用反透视变换，使用相机内参和畸变系数，可以计算归一化相机中表示的图像点

FileStorage fs( samples::findFile( intrinsicsPath ), FileStorage::READ);
Mat cameraMatrix, distCoeffs;
fs["camera_matrix"] >> cameraMatrix;
fs["distortion_coefficients"] >> distCoeffs;

vector<Point2f> imagePoints;
undistortPoints(corners, imagePoints, cameraMatrix, distCoeffs);

然后可以利用以下方式计算单应性：

Mat H = findHomography(objectPointsPlanar, imagePoints);
cout << "H:\n" << H << endl;

从单应性矩阵中快速获取位姿的解决方案是（请参阅 5）

    // 归一化以确保 ||c1|| = 1
    double norm = sqrt(H.at<double>(0,0)*H.at<double>(0,0) +
H.at<double>(1,0)*H.at<double>(1,0) +
H.at<double>(2,0)*H.at<double>(2,0));
 
H /= norm;
Mat c1 = H.col(0);
Mat c2 = H.col(1);
Mat c3 = c1.cross(c2);
 
Mat tvec = H.col(2);
Mat R(3, 3, CV_64F);
 
    for (int i = 0; i < 3; i++)
    {
R.at<double>(i,0) = c1.at<double>(i,0);
R.at<double>(i,1) = c2.at<double>(i,0);
R.at<double>(i,2) = c3.at<double>(i,0);
    }

\[

\[

这是一个快速解法（另请参阅2），因为它不能确保生成结果的旋转矩阵会是正交的且标度是由将第一列规范化为 1 而粗略估计的。

采用适当的旋转矩阵（包含旋转矩阵的属性）的解决方案包括应用极分解或正交化旋转矩阵（关于极分解的更多信息，请参阅6或7或8或9）

cout << "R (极分解前):\n" << R << "\ndet(R): " << determinant(R) << endl;
Mat_<double> W, U, Vt;
SVDecomp(R, W, U, Vt);
R = U*Vt;
    double det = determinant(R);
    if (det < 0)
    {
Vt.at<double>(2,0) *= -1;
Vt.at<double>(2,1) *= -1;
Vt.at<double>(2,2) *= -1;
 
R = U*Vt;
    }
cout << "R (极分解后):\n" << R << "\ndet(R): " << determinant(R) << endl;

为了检查结果，将使用估计的摄像头姿态将目标帧投射到图像中并显示出来。

示例 2：透视校正

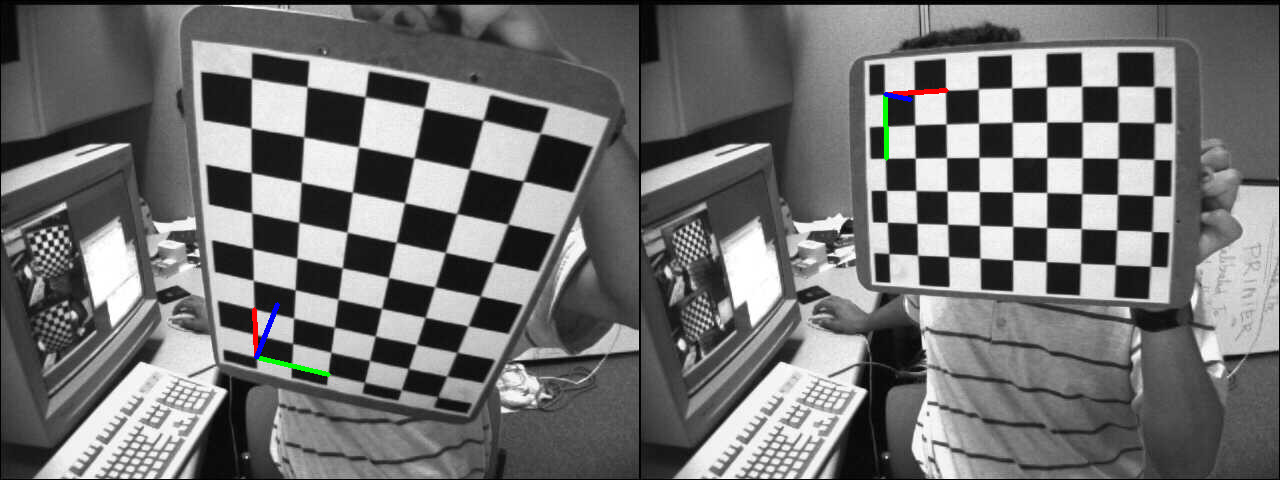
本例中，将通过计算将源点映射到所需点单应性来将源图像转换成所需透视图。下图显示了源图像（左）和我们希望转换成所需棋盘图的棋盘视图（右）。

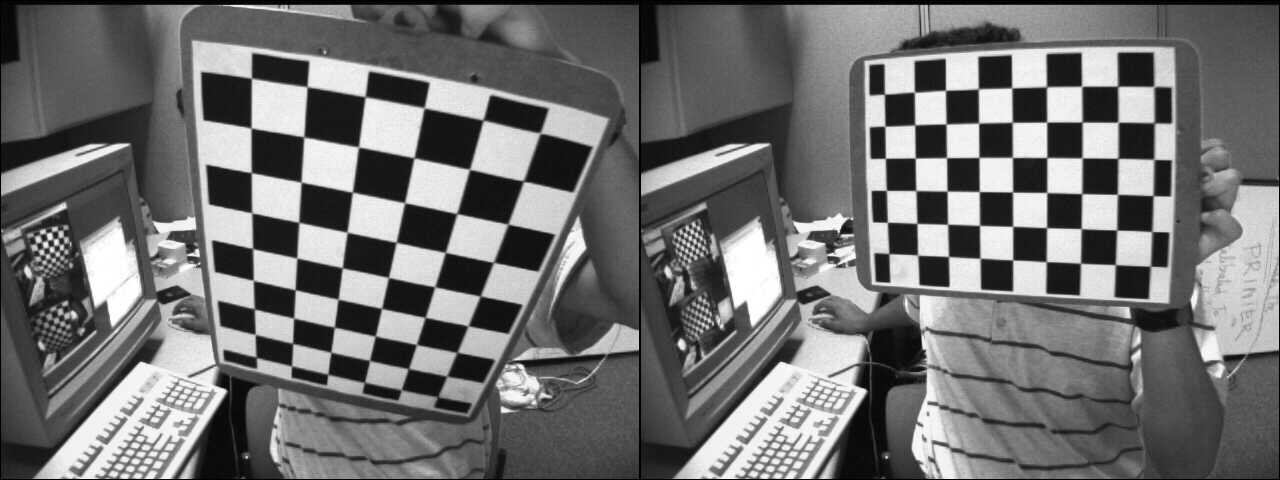
源和所需视图

第一步是检测源和所需图像中的棋盘格角点。

C++

vector<Point2f> corners1, corners2;
    bool found1 = findChessboardCorners(img1, patternSize, corners1);
    bool found2 = findChessboardCorners(img2, patternSize, corners2);

Python

ret1, corners1 = cv.findChessboardCorners(img1, patternSize)
ret2, corners2 = cv.findChessboardCorners(img2, patternSize)

Java

MatOfPoint2f corners1 = new MatOfPoint2f(), corners2 = new MatOfPoint2f();
        boolean found1 = Calib3d.findChessboardCorners(img1, new Size(9, 6), corners1 );
        boolean found2 = Calib3d.findChessboardCorners(img2, new Size(9, 6), corners2 );

齐次变换很容易通过以下公式估计得到：

C++

Mat H = findHomography(corners1, corners2);
cout << "H:\n" << H << endl;

Python

H, _ = cv.findHomography(corners1, corners2)
print(H)

Java

Mat H = new Mat();
H = Calib3d.findHomography(corners1, corners2);
System.out.println(H.dump());

为了将源棋盘视图扭曲成期望的棋盘视图，我们使用 cv::warpPerspective

C++

Mat img1_warp;
warpPerspective(img1, img1_warp, H, img1.size());

Python

img1_warp = cv.warpPerspective(img1, H, (img1.shape[1], img1.shape[0]))

Java

Mat img1_warp = new Mat();
Imgproc.warpPerspective(img1, img1_warp, H, img1.size());

生成的图像为：

计算由齐次变换转换后的源角点坐标：

C++

Mat img_draw_matches;
hconcat(img1, img2, img_draw_matches);
    for (size_t i = 0; i < corners1.size(); i++)
    {
Mat pt1 = (Mat_<double>(3,1) << corners1[i].x, corners1[i].y, 1);
Mat pt2 = H * pt1;
pt2 /= pt2.at<double>(2);
 
Point end( (int) (img1.cols + pt2.at<double>(0)), (int) pt2.at<double>(1) );
line(img_draw_matches, corners1[i], end, randomColor(rng), 2);
    }
 
imshow("Draw matches", img_draw_matches);
waitKey();

Python

img_draw_matches = cv.hconcat([img1, img2])
    对于 i 在 range(len(corners1))
pt1 = np.array([corners1[i][0], corners1[i][1], 1])
pt1 = pt1.reshape(3, 1)
pt2 = np.dot(H, pt1)
pt2 = pt2/pt2[2]
end = (int(img1.shape[1] + pt2[0]), int(pt2[1]))
        cv.line(img_draw_matches, tuple([int(j) 对于 j 在 corners1[i]]), end, randomColor(), 2)
 
    cv.imshow("绘制匹配项", img_draw_matches)
    cv.waitKey(0)

Java

Mat img_draw_matches = new Mat();
list2.add(img1);
list2.add(img2);
Core.hconcat(list2, img_draw_matches);
Point []corners1Arr = corners1.toArray();
 
        对于 (int i = 0 ; i < corners1Arr.length; i++) {
Mat pt1 = new Mat(3, 1, CvType.CV_64FC1), pt2 = new Mat();
pt1.put(0, 0, corners1Arr[i].x, corners1Arr[i].y, 1 );
 
Core.gemm(H, pt1, 1, new Mat(), 0, pt2);
            double[] data = pt2.get(2, 0);
Core.divide(pt2, new Scalar(data[0]), pt2);
 
            double[] data1 =pt2.get(0, 0);
            double[] data2 = pt2.get(1, 0);
Point end = new Point((int)(img1.cols()+ data1[0]), (int)data2[0]);
Imgproc.line(img_draw_matches, corners1Arr[i], end, RandomColor(), 2);
        }
 
HighGui.imshow("绘制匹配项", img_draw_matches);
HighGui.waitKey(0);

为了检查计算的正确性，显示匹配线

演示 3：来自相机位移的单应性

单应性关联两个平面之间的变换，并且可以检索出允许从第一个平面视图转到第二个平面视图的相应相机位移（有关更多信息，请参阅 [180]）。在进入计算相机位移的单应性的细节之前，需要回顾一下相机位姿和齐次变换。

函数 cv::solvePnP 允许从 3D 物体点（在物体坐标系中表示的点）和投影的 2D 图像点（图像中看到的物体点）的对应关系中计算摄像机姿态。需要内参和畸变系数（请参阅相机标定过程）。

\[ \begin{align*} s \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} &= \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \end{bmatrix} \begin{bmatrix} X_o \\ Y_o \\ Z_o \\ 1 \end{bmatrix} \\ &= \mathbf{K} \hspace{0.2em} ^{c}\mathbf{M}_o \begin{bmatrix} X_o \\ Y_o \\ Z_o \\ 1 \end{bmatrix} \end{align*} \]

\( \mathbf{K} \) 是内参矩阵，\( ^{c}\mathbf{M}_o \) 是摄影机位姿。 cv::solvePnP 的输出恰好是：rvec 是罗德里格斯旋转向量，tvec 是平移向量。

\( ^{c}\mathbf{M}_o \) 可以用齐次形式表示，并且能够将表示在物体坐标系中的点坐标转换成摄影机坐标系

\[ \begin{align*} \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \end{bmatrix} &= \hspace{0.2em} ^{c}\mathbf{M}_o \begin{bmatrix} X_o \\ Y_o \\ Z_o \\ 1 \end{bmatrix} \\ &= \begin{bmatrix} ^{c}\mathbf{R}_o & ^{c}\mathbf{t}_o \\ 0_{1\times3} & 1 \end{bmatrix} \begin{bmatrix} X_o \\ Y_o \\ Z_o \\ 1 \end{bmatrix} \\ &= \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X_o \\ Y_o \\ Z_o \\ 1 \end{bmatrix} \end{align*} \]

通过矩阵乘法可以轻松地将表示在一个坐标系中的点坐标转换成另一个坐标系

• \( ^{c_1}\mathbf{M}_o \) 是相机 1 的摄影机位姿
• \( ^{c_2}\mathbf{M}_o \) 是相机 2 的摄影机位姿

要将表示在相机 1 坐标系中的 3D 点坐标转换成相机 2 坐标系中的点坐标

\[ ^{c_2}\mathbf{M}_{c_1} = \hspace{0.2em} ^{c_2}\mathbf{M}_{o} \cdot \hspace{0.1em} ^{o}\mathbf{M}_{c_1} = \hspace{0.2em} ^{c_2}\mathbf{M}_{o} \cdot \hspace{0.1em} \left( ^{c_1}\mathbf{M}_{o} \right )^{-1} = \begin{bmatrix} ^{c_2}\mathbf{R}_{o} & ^{c_2}\mathbf{t}_{o} \\ 0_{3 \times 1} & 1 \end{bmatrix} \cdot \begin{bmatrix} ^{c_1}\mathbf{R}_{o}^T & - \hspace{0.2em} ^{c_1}\mathbf{R}_{o}^T \cdot \hspace{0.2em} ^{c_1}\mathbf{t}_{o} \\ 0_{1 \times 3} & 1 \end{bmatrix} \]

在此示例中，我们将根据棋盘格图案计算两个摄影机位姿之间的摄像机位移。第一步是为这两个图像计算摄影机位姿

vector<Point2f> corners1, corners2;
    bool found1 = findChessboardCorners(img1, patternSize, corners1);
    bool found2 = findChessboardCorners(img2, patternSize, corners2);
 
    if (!found1 || !found2)
    {
cout << "错误，在两个图像中都找不到棋盘角点。" << endl;
        return;
    }
 
vector<Point3f> objectPoints;
calcChessboardCorners(patternSize, squareSize, objectPoints);
 
FileStorage fs( samples::findFile( intrinsicsPath ), FileStorage::READ);
Mat cameraMatrix, distCoeffs;
fs["camera_matrix"] >> cameraMatrix;
fs["distortion_coefficients"] >> distCoeffs;
 
Mat rvec1, tvec1;
solvePnP(objectPoints, corners1, cameraMatrix, distCoeffs, rvec1, tvec1);
Mat rvec2, tvec2;
solvePnP(objectPoints, corners2, cameraMatrix, distCoeffs, rvec2, tvec2);

可以根据上述公式计算摄影机位移

void computeC2MC1(const Mat &R1, const Mat &tvec1, const Mat &R2, const Mat &tvec2,
Mat &R_1to2, Mat &tvec_1to2)
{
    //c2Mc1 = c2Mo * oMc1 = c2Mo * c1Mo.inv()
R_1to2 = R2 * R1.t();
tvec_1to2 = R2 * (-R1.t()*tvec1) + tvec2;
}

根据摄影机位移计算的与具体平面相关的单应性

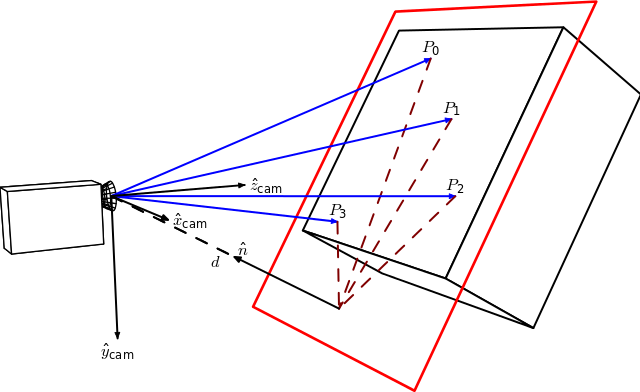
来自 Homography-transl.svg: Per Rosengren derivative work: Appoose (Homography-transl.svg) [CC BY 3.0 (http://creativecommons.org/licenses/by/3.0)], 来自 Wikimedia Commons

在此图中，n 是平面的法向量，d 是摄影机坐标系与平面之间的距离，沿平面的法向量方向。从摄影机位移计算单应性的方程：

\[ ^{2}\mathbf{H}_{1} = \hspace{0.2em} ^{2}\mathbf{R}_{1} - \hspace{0.1em} \frac{^{2}\mathbf{t}_{1} \cdot \hspace{0.1em} ^{1}\mathbf{n}^\top}{^1d} \]

其中，\( ^{2}\mathbf{H}_{1} \) 是会将第一个摄影机坐标系中的点映射到第二个摄影机坐标系中的对应点的单应性矩阵，\( ^{2}\mathbf{R}_{1} = \hspace{0.2em} ^{c_2}\mathbf{R}_{o} \cdot \hspace{0.1em} ^{c_1}\mathbf{R}_{o}^{\top} \) 是表示两个摄影机坐标系之间旋转的旋转矩阵，\( ^{2}\mathbf{t}_{1} = \hspace{0.2em} ^{c_2}\mathbf{R}_{o} \cdot \left( - \hspace{0.1em} ^{c_1}\mathbf{R}_{o}^{\top} \cdot \hspace{0.1em} ^{c_1}\mathbf{t}_{o} \right ) + \hspace{0.1em} ^{c_2}\mathbf{t}_{o} \) 是两个摄影机坐标系之间的平移向量。

这里，法向量 n 是摄影机坐标系 1 中表达的平面法向量，可以用 2 个向量的叉乘（使用位于该平面的 3 个非共线点）或直接使用

Mat normal = (Mat_<double>(3,1) << 0, 0, 1);
Mat normal1 = R1*normal;

距离 d 可以计算为平面法向量与平面上一点之间的点积，或者通过计算平面方程并使用 D 系数

Mat origin(3, 1, CV_64F, Scalar(0));
Mat origin1 = R1*origin + tvec1;
    double d_inv1 = 1.0 / normal1.dot(origin1);

投影单应性矩阵 \( \textbf{G} \) 可以使用内参矩阵 \( \textbf{K} \) 从欧几里得单应矩阵 \( \textbf{H} \) 计算（参见 [180]），此处假定两幅平面视图使用的是同一部相机。

\[ \textbf{G} = \gamma \textbf{K} \textbf{H} \textbf{K}^{-1} \]

Mat computeHomography(const Mat &R_1to2, const Mat &tvec_1to2, const double d_inv, const Mat &normal)
{
Mat homography = R_1to2 + d_inv * tvec_1to2*normal.t();
    return homography;
}

在我们的案例中，棋盘格的 Z 轴朝向物体内部，而在单应性图像中它朝向外部。这只是一个正负号问题

\[ ^{2}\mathbf{H}_{1} = \hspace{0.2em} ^{2}\mathbf{R}_{1} + \hspace{0.1em} \frac{^{2}\mathbf{t}_{1} \cdot \hspace{0.1em} ^{1}\mathbf{n}^\top}{^1d} \]

Mat homography_euclidean = computeHomography(R_1to2, t_1to2, d_inv1, normal1);
Mat homography = cameraMatrix * homography_euclidean * cameraMatrix.inv();
 
homography /= homography.at<double>(2,2);
homography_euclidean /= homography_euclidean.at<double>(2,2);

我们现在将比较从相机位移计算的投影单应性与用 cv::findHomography 估计出的那个。

findHomography H
[0.32903393332201, -1.244138808862929, 536.4769088231476;
 0.6969763913334046, -0.08935909072571542, -80.34068504082403;
 0.00040511729592961, -0.001079740100565013, 0.9999999999999999]
 
相机位移单应
[0.4160569997384721, -1.306889006892538, 553.7055461075881;
 0.7917584252773352, -0.06341244158456338, -108.2770029401219;
 0.0005926357240956578, -0.001020651672127799, 1]

单应矩阵相似。如果我们使用两个单应矩阵对图像 1 进行翘曲

左：使用估计出的单应矩阵翘曲的图像。右：使用从相机位移计算出的单应矩阵翘曲的图像。

从视觉上看，难以区分使用从相机位移计算出的单应矩阵和使用 cv::findHomography 函数估计出的单应矩阵翘曲图像的结果。

练习

此演示向您展示如何从两个相机姿态计算单应性变换。尝试执行相同的操作，但这次是计算 N 个中间单应。不是计算一个单应直接将源图像翘曲到所需的相机视点，而是执行 N 个翘曲操作以查看不同的变换操作。

您应该会得到类似以下内容的结果

前三幅图像显示在三个不同插值相机视点翘曲的源图像。第 4 幅图像显示了在最终相机视点处翘曲的源图像和所需图像之间的“错误图像”。

演示 4：分解单应矩阵

OpenCV 3 包含函数 cv::decomposeHomographyMat，它允许将单应矩阵分解为一组旋转、平移和法线平面。首先，我们将分解从相机位移计算出的单应矩阵

Mat homography_euclidean = computeHomography(R_1to2, t_1to2, d_inv1, normal1);
Mat homography = cameraMatrix * homography_euclidean * cameraMatrix.inv();
 
homography /= homography.at<double>(2,2);
homography_euclidean /= homography_euclidean.at<double>(2,2);

下列是 cv::decomposeHomographyMat 的结果：

vector<Mat> Rs_decomp, ts_decomp, normals_decomp;
    int solutions = decomposeHomographyMat(homography, cameraMatrix, Rs_decomp, ts_decomp, normals_decomp);
cout << "由相机位移计算出的分解单应矩阵："  << endl << endl;
    for (int i = 0; i < solutions; i++)
    {
      double factor_d1 = 1.0 / d_inv1;
Mat rvec_decomp;
Rodrigues(Rs_decomp[i], rvec_decomp);
cout << "解决方案 " << i << ":" << endl;
cout << "单应矩阵分解中的 rvec： " << rvec_decomp.t() << endl;
cout << "相机位移中的 rvec： " << rvec_1to2.t() << endl;
cout << "单应分解中的 tvec： " << ts_decomp[i].t() << " 按 d 缩小后： " << factor_d1 * ts_decomp[i].t() << endl;
cout << "相机位移中的 tvec： " << t_1to2.t() << endl;
cout << "单应分解中的平面法向量： " << normals_decomp[i].t() << endl;
cout << "相机 1 姿势中的平面法向量： " << normal1.t() << endl << endl;
    }

解决方案 0
单应矩阵分解中的 rvec： [-0.0919829920641369, -0.5372581036567992, 1.310868863540717]
相机位移中的 rvec： [-0.09198299206413783, -0.5372581036567995, 1.310868863540717]
单应分解中的 tvec： [-0.7747961019053186, -0.02751124463434032, -0.6791980037590677] 按 d 缩小后： [-0.1578091561210742, -0.005603443652993778, -0.1383378976078466]
相机位移中的 tvec： [0.1578091561210745, 0.005603443652993617, 0.1383378976078466]
单应分解中的平面法向量： [-0.1973513139420648, 0.6283451996579074, -0.7524857267431757]
相机 1 姿势中的平面法向量： [0.1973513139420654, -0.6283451996579068, 0.752485726743176]
 
解决方案 1
单应矩阵分解中的 rvec： [-0.0919829920641369, -0.5372581036567992, 1.310868863540717]
相机位移中的 rvec： [-0.09198299206413783, -0.5372581036567995, 1.310868863540717]
单应分解中的 tvec： [0.7747961019053186, 0.02751124463434032, 0.6791980037590677] 按 d 缩小后： [0.1578091561210742, 0.005603443652993778, 0.1383378976078466]
相机位移中的 tvec： [0.1578091561210745, 0.005603443652993617, 0.1383378976078466]
单应分解中的平面法向量： [0.1973513139420648, -0.6283451996579074, 0.7524857267431757]
相机 1 姿势中的平面法向量： [0.1973513139420654, -0.6283451996579068, 0.752485726743176]
 
解决方案 2
单应分解中的 rvec： [0.1053487907109967, -0.1561929144786397, 1.401356552358475]
相机位移中的 rvec： [-0.09198299206413783, -0.5372581036567995, 1.310868863540717]
单应分解中的 tvec： [-0.4666552552894618, 0.1050032934770042, -0.913007654671646] 按 d 缩小后： [-0.0950475510338766, 0.02138689274867372, -0.1859598508065552]
相机位移中的 tvec： [0.1578091561210745, 0.005603443652993617, 0.1383378976078466]
单应分解中的平面法向量： [-0.3131715472900788, 0.8421206145721947, -0.4390403768225507]
相机 1 姿势中的平面法向量： [0.1973513139420654, -0.6283451996579068, 0.752485726743176]
 
解决方案 3
单应分解中的 rvec： [0.1053487907109967, -0.1561929144786397, 1.401356552358475]
相机位移中的 rvec： [-0.09198299206413783, -0.5372581036567995, 1.310868863540717]
单应分解中的 tvec： [0.4666552552894618, -0.1050032934770042, 0.913007654671646] 按 d 缩小后： [0.0950475510338766, -0.02138689274867372, 0.1859598508065552]
相机位移中的 tvec： [0.1578091561210745, 0.005603443652993617, 0.1383378976078466]
单应分解中的平面法向量： [0.3131715472900788, -0.
相机 1 姿势中的平面法向量： [0.1973513139420654, -0.6283451996579068, 0.752485726743176]

同态矩阵分解的结果只能恢复到一个实际对应于法线单位长度距离d的比例因子。正如你所看到的，有一个解几乎与计算的相机位移完全匹配。正如文档中所述

如果通过应用正深度约束（所有点都必须在相机前面）提供点对应关系，则至少两个解还可以是无效的。

由于分解的结果是相机位移，如果我们有初始相机位姿\( ^{c_1}\mathbf{M}_{o} \)，我们可以计算当前相机位姿\( ^{c_2}\mathbf{M}_{o} = \hspace{0.2em} ^{c_2}\mathbf{M}_{c_1} \cdot \hspace{0.1em} ^{c_1}\mathbf{M}_{o} \)并测试属于平面的三维物体点是否投影在相机前面。如果我们知道在相机 1 位姿下表达的平面法线，另一个解可以保留具有最接近法线的解。

相同的情况，但同态矩阵使用cv::findHomography估计

解决方案 0
来自同态矩阵分解的rvec：[0.1552207729599141，-0.152132696119647，1.323678695078694]
相机位移中的 rvec： [-0.09198299206413783, -0.5372581036567995, 1.310868863540717]
来自同态矩阵分解的tvec：[-0.4482361704818117，0.02485247635491922，-1.034409687207331] 和按照d缩放：[-0.09129598307571339，0.005061910238634657，-0.2106868109173855]
相机位移中的 tvec： [0.1578091561210745, 0.005603443652993617, 0.1383378976078466]
来自同态矩阵分解的平面法线：[-0.1384902722707529，0.9063331452766947，-0.3992250922214516]
相机 1 姿势中的平面法向量： [0.1973513139420654, -0.6283451996579068, 0.752485726743176]
 
解决方案 1
来自同态矩阵分解的rvec：[0.1552207729599141，-0.152132696119647，1.323678695078694]
相机位移中的 rvec： [-0.09198299206413783, -0.5372581036567995, 1.310868863540717]
来自同态矩阵分解的tvec：[0.4482361704818117，-0.02485247635491922，1.034409687207331] 和按照d缩放：[0.09129598307571339，-0.005061910238634657，0.2106868109173855]
相机位移中的 tvec： [0.1578091561210745, 0.005603443652993617, 0.1383378976078466]
来自同态矩阵分解的平面法线：[0.1384902722707529，-0.9063331452766947，0.3992250922214516]
相机 1 姿势中的平面法向量： [0.1973513139420654, -0.6283451996579068, 0.752485726743176]
 
解决方案 2
来自同态矩阵分解的rvec：[-0.2886605671759886，-0.521049903923871，1.381242030882511]
相机位移中的 rvec： [-0.09198299206413783, -0.5372581036567995, 1.310868863540717]
来自同态矩阵分解的tvec：[-0.8705961357284295，0.1353018038908477，-0.7037702049789747] 和按照d缩放：[-0.177321544550518，0.02755804196893467，-0.1433427218822783]
相机位移中的 tvec： [0.1578091561210745, 0.005603443652993617, 0.1383378976078466]
来自同态矩阵分解的平面法线：[-0.2284582117722427，0.6009247303964522，-0.7659610393954643]
相机 1 姿势中的平面法向量： [0.1973513139420654, -0.6283451996579068, 0.752485726743176]
 
解决方案 3
来自同态矩阵分解的rvec：[-0.2886605671759886，-0.521049903923871，1.381242030882511]
相机位移中的 rvec： [-0.09198299206413783, -0.5372581036567995, 1.310868863540717]
来自同态矩阵分解的tvec：[0.8705961357284295，-0.1353018038908477，0.7037702049789747] 和按照d缩放：[0.177321544550518，-0.02755804196893467，0.1433427218822783]
相机位移中的 tvec： [0.1578091561210745, 0.005603443652993617, 0.1383378976078466]
来自同态矩阵分解的平面法线：[0.2284582117722427，-0.6009247303964522，0.7659610393954643]
相机 1 姿势中的平面法向量： [0.1973513139420654, -0.6283451996579068, 0.752485726743176]

同样也有一种解与计算的相机位移相匹配。

演示 5：根据旋转相机进行基本全景拼接

注意

本示例旨在说明基于相机纯旋转运动的图像拼接概念，不应用于拼接全景图像。拼接模块提供了一个完整的管道来拼接图像。

同态变换仅适用于平面结构。但在旋转相机（在相机投影轴上纯旋转，无平移）的情况下，可以考虑任意的真实世界（见前文）。

然后可以使用旋转变换和相机内部参数来计算同态，如下所示（例如，参见10）

\[ s \begin{bmatrix} x^{'} \\ y^{'} \\ 1 \end{bmatrix} = \bf{K} \hspace{0.1em} \bf{R} \hspace{0.1em} \bf{K}^{-1} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \]

为了说明，我们使用了 Blender，一种免费且开源的 3D 计算机图形软件，以生成两个仅相互之间进行旋转变换的摄像机视图。有关如何使用 Blender 检索与世界相关的摄像机内参和3x4外参矩阵的更多信息，请参阅11（需要额外的变换才能在摄像机和对象帧之间进行变换）。

下图显示了 Suzanne 模型的两个生成视图，仅进行了旋转变换

使用已知的相关摄像机姿态和内参可以计算两个视图之间的相对旋转

C++

Mat R1 = c1Mo(Range(0,3), Range(0,3));
Mat R2 = c2Mo(Range(0,3), Range(0,3));

Python

R1 = c1Mo[0:3, 0:3]
R2 = c2Mo[0:3, 0:3]

Java

Range rowRange = new Range(0,3);
Range colRange = new Range(0,3);

C++

    //c1Mo * oMc2
Mat R_2to1 = R1*R2.t();

Python

R2 = R2.transpose()
R_2to1 = np.dot(R1,R2)

Java

        //c1Mo * oMc2
Mat R1 = new Mat(c1Mo, rowRange, colRange);
Mat R2 = new Mat(c2Mo, rowRange, colRange);
Mat R_2to1 = new Mat();
Core.gemm(R1, R2.t(), 1, new Mat(), 0, R_2to1 );

这里，第二个图像将相对于第一个图像拼接。齐次变换可以使用上述公式进行计算

C++

Mat H = cameraMatrix * R_2to1 * cameraMatrix.inv();
H /= H.at<double>(2,2);
cout << "H:\n" << H << endl;

Python

H = cameraMatrix.dot(R_2to1).dot(np.linalg.inv(cameraMatrix))
H = H / H[2][2]

Java

Mat tmp = new Mat(), H = new Mat();
Core.gemm(cameraMatrix, R_2to1, 1, new Mat(), 0, tmp);
Core.gemm(tmp, cameraMatrix.inv(), 1, new Mat(), 0, H);
Scalar s = new Scalar(H.get(2, 2)[0]);
Core.divide(H, s, H);
System.out.println(H.dump());

拼接简单地通过

C++

Mat img_stitch;
warpPerspective(img2, img_stitch, H, Size(img2.cols*2, img2.rows));
Mat half = img_stitch(Rect(0, 0, img1.cols, img1.rows));
img1.copyTo(half);

Python

img_stitch = cv.warpPerspective(img2, H, (img2.shape[1]*2, img2.shape[0]))
img_stitch[0:img1.shape[0], 0:img1.shape[1]] = img1

Java

Mat img_stitch = new Mat();
Imgproc.warpPerspective(img2, img_stitch, H, new Size(img2.cols()*2, img2.rows()) );
Mat half = new Mat();
half = new Mat(img_stitch, new Rect(0, 0, img1.cols(), img1.rows()));
img1.copyTo(half);

生成图像为

其他参考文献

• 1. 讲座 16：平面齐次变换，Robert Collins
• 2. 2D 透视变换（单应性变换）, 克里斯蒂亚诺·加瓦、加布里埃尔·布莱塞
• 3. 计算机视觉：算法和应用, 理查德·塞泽里斯基
• 4. 用于视觉跟踪和平面标记的逐步相机位姿估计
• 5. 来自单应性的姿态估计
• 6. 极分解（在连续介质力学中）
• 7. 第 3 章 - 3.1.2 从矩阵到旋转 - 定理 3.1（从矩阵 K 估计旋转的最小二乘法）
• 8. 与奇异值分解的个人访谈, 马坦·加维什
• 9. 卡巴施算法，计算最优旋转矩阵
• 10. 单应性变换, 格哈德·罗斯博士
• 11. 来自 Blender 相机的 3x4 相机矩阵