import org.opencv.core.*;
import org.opencv.core.Point;
import org.opencv.highgui.HighGui;
import org.opencv.imgcodecs.Imgcodecs;
import org.opencv.imgproc.Imgproc;
class HoughLinesRun {
public void run(String[] args) {
Mat dst = new Mat(), cdst = new Mat(), cdstP;
String default_file = "../../../../data/sudoku.png";
String filename = ((args.length > 0) ? args[0] : default_file);
Mat src = Imgcodecs.imread(filename, Imgcodecs.IMREAD_GRAYSCALE);
if( src.empty() ) {
System.out.println("Error opening image!");
System.out.println("Program Arguments: [image_name -- default "
+ default_file +"] \n");
System.exit(-1);
}
Imgproc.Canny(src, dst, 50, 200, 3, false);
Imgproc.cvtColor(dst, cdst, Imgproc.COLOR_GRAY2BGR);
cdstP = cdst.clone();
Mat lines = new Mat();
Imgproc.HoughLines(dst, lines, 1, Math.PI/180, 150);
for (int x = 0; x < lines.rows(); x++) {
double rho = lines.get(x, 0)[0],
theta = lines.get(x, 0)[1];
double a = Math.cos(theta), b = Math.sin(theta);
double x0 = a*rho, y0 = b*rho;
Point pt1 = new Point(Math.round(x0 + 1000*(-b)), Math.round(y0 + 1000*(a)));
Point pt2 = new Point(Math.round(x0 - 1000*(-b)), Math.round(y0 - 1000*(a)));
Imgproc.line(cdst, pt1, pt2, new Scalar(0, 0, 255), 3, Imgproc.LINE_AA, 0);
}
Mat linesP = new Mat();
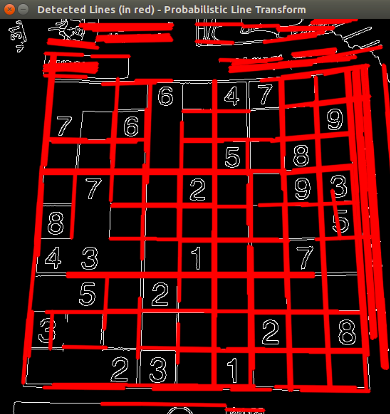
Imgproc.HoughLinesP(dst, linesP, 1, Math.PI/180, 50, 50, 10);
for (int x = 0; x < linesP.rows(); x++) {
double[] l = linesP.get(x, 0);
Imgproc.line(cdstP, new Point(l[0], l[1]), new Point(l[2], l[3]), new Scalar(0, 0, 255), 3, Imgproc.LINE_AA, 0);
}
HighGui.imshow("Source", src);
HighGui.imshow("Detected Lines (in red) - Standard Hough Line Transform", cdst);
HighGui.imshow("Detected Lines (in red) - Probabilistic Line Transform", cdstP);
HighGui.waitKey();
System.exit(0);
}
}
public static void main(String[] args) {
System.loadLibrary(Core.NATIVE_LIBRARY_NAME);
new HoughLinesRun().run(args);
}
}
void HoughLines(InputArray image, OutputArray lines, double rho, double theta, int threshold, double srn=0, double stn=0, double min_theta=0, double max_theta=CV_PI, bool use_edgeval=false)
使用标准霍夫变换在二值图像中查找直线。