目标

在本教程中，您将学习如何

什么是支持向量机（SVM）？

支持向量机（SVM）是一种判别分类器，其正式定义为一个分离超平面。换句话说，给定有标签的训练数据（监督学习），该算法会输出一个最优超平面，用于对新样本进行分类。

所获得的超平面在何种意义上是“最优”的？让我们考虑以下简单问题：

对于一个线性可分的二维点集，这些点属于两个类别之一，请找到一条分离直线。

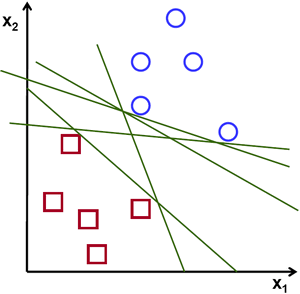
注意: 在这个例子中，我们处理的是笛卡尔平面中的直线和点，而不是高维空间中的超平面和向量。这是一个简化的问题。重要的是要理解，这样做只是因为我们更容易从易于想象的例子中建立直观认识。然而，相同的概念也适用于分类任务，其中待分类的样本位于维度高于二的空间中。

在上图中，您可以看到存在多条直线可以解决该问题。其中是否有哪一条比其他的更好？我们可以凭直觉定义一个标准来评估直线的价值：如果一条直线过于靠近点，则它不好，因为它对噪声敏感，并且无法正确泛化。因此，我们的目标应该是找到一条尽可能远离所有点的直线。

因此，SVM算法的操作基于找到一个超平面，该超平面能提供到训练样本的最大最小距离。这个距离的两倍在SVM理论中被赋予了重要的名称：间隔（margin）。因此，最优分离超平面会最大化训练数据的间隔。

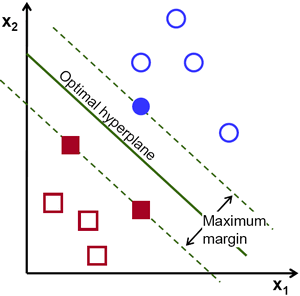
让我们引入用于正式定义超平面的符号：

\[f(x) = \beta_{0} + \beta^{T} x,\]

其中 \(\beta\) 被称为权重向量，\(\beta_{0}\) 被称为偏置。

注意: 关于这一点和超平面的更深入描述，您可以在T. Hastie、R. Tibshirani和J. H. Friedman所著的《统计学习的要素》（Elements of Statistical Learning）一书的4.5节（分离超平面）中找到 ([276])。

通过对 \(\beta\) 和 \(\beta_{0}\) 进行缩放，最优超平面可以用无数种不同的方式表示。按照惯例，在所有可能的超平面表示中，选择的是：

\[|\beta_{0} + \beta^{T} x| = 1\]

其中 \(x\) 象征着离超平面最近的训练样本。通常，离超平面最近的训练样本被称为支持向量（support vectors）。这种表示方式被称为规范超平面（canonical hyperplane）。

现在，我们使用几何学中关于点 \(x\) 与超平面 \((\beta, \beta_{0})\) 之间距离的结果：

\[\mathrm{distance} = \frac{|\beta_{0} + \beta^{T} x|}{||\beta||}.\]

特别是对于规范超平面，分子等于1，到支持向量的距离为：

\[\mathrm{distance}_{\text{ support vectors}} = \frac{|\beta_{0} + \beta^{T} x|}{||\beta||} = \frac{1}{||\beta||}.\]

回想一下前一节中引入的间隔，这里表示为 \(M\)，它是到最近样本距离的两倍：

\[M = \frac{2}{||\beta||}\]

最后，最大化 \(M\) 的问题等价于在某些约束条件下最小化函数 \(L(\beta)\) 的问题。这些约束条件模拟了超平面正确分类所有训练样本 \(x_{i}\) 的要求。形式上：

\[\min_{\beta, \beta_{0}} L(\beta) = \frac{1}{2}||\beta||^{2} \text{ 满足 } y_{i}(\beta^{T} x_{i} + \beta_{0}) \geq 1 \text{ } \forall i,\]

其中 \(y_{i}\) 代表每个训练样本的标签。

这是一个拉格朗日优化问题，可以通过使用拉格朗日乘数来求解，以获得最优超平面的权重向量 \(\beta\) 和偏置 \(\beta_{0}\)。

本练习的训练数据由一组带有标签的二维点组成，它们属于两个不同类别中的一个；其中一个类别包含一个点，另一个类别包含三个点。

后续将使用的函数 cv::ml::SVM::train 要求训练数据存储为浮点型的 cv::Mat 对象。因此，我们从上面定义的数组中创建这些对象：

设置SVM参数

在本教程中，我们介绍了SVM在最简单情况下的理论，即训练样本分为两个线性可分的类别。然而，SVM可以用于各种各样的问题（例如，非线性可分数据的问题，使用核函数提高样本维度的SVM等）。因此，在训练SVM之前，我们必须定义一些参数。这些参数存储在 cv::ml::SVM 类的一个对象中。

在这里

SVM 类型。我们在此选择 C_SVC 类型，它可用于 n 类分类 (n \(\geq\) 2)。这种类型的重要特性是它能处理不完美分离的类别（即，当训练数据非线性可分时）。此特性在这里并不重要，因为数据是线性可分的，我们选择此SVM类型仅因为它最常用。
SVM 核函数类型。我们没有讨论核函数，因为它们对我们正在处理的训练数据不感兴趣。然而，现在让我们简要解释一下核函数背后的主要思想。它是一种对训练数据进行的映射，旨在提高其与线性可分数据集的相似性。这种映射通过增加数据的维度来实现，并使用核函数高效地完成。我们在这里选择 LINEAR 类型，这意味着不进行任何映射。此参数使用 cv::ml::SVM::setKernel 定义。
算法终止标准。SVM 训练过程是通过迭代方式解决一个受约束的二次优化问题来实现的。这里我们指定了最大迭代次数和容忍误差，这样即使最优超平面尚未计算出来，我们也允许算法在更少的步骤中完成。此参数在 cv::TermCriteria 结构中定义。
训练SVM 我们调用方法 cv::ml::SVM::train 来构建SVM模型。

SVM分类的区域

方法 cv::ml::SVM::predict 用于使用训练好的SVM对输入样本进行分类。在此示例中，我们使用此方法根据SVM的预测结果对空间进行着色。换句话说，遍历图像并将其像素解释为笛卡尔平面上的点。每个点根据SVM预测的类别进行着色；如果预测类别为1，则为绿色；如果预测类别为-1，则为蓝色。

支持向量

我们这里使用了几个方法来获取关于支持向量的信息。方法 cv::ml::SVM::getSupportVectors 获取所有支持向量。我们在这里使用这些方法来找到作为支持向量的训练样本并将其突出显示。


原始作者	Fernando Iglesias García
兼容性	OpenCV >= 3.0