 |
OpenCV 4.10.0
开源计算机视觉
|
 |
OpenCV 4.10.0
开源计算机视觉
|
OpenCV(开源计算机视觉) 是一个流行的计算机视觉库,由 英特尔 于 1999 年启动。该跨平台库专注于实时图像处理,并包含最新计算机视觉算法的免专利实现。2008 年,Willow Garage 接管了支持工作,OpenCV 2.3.1 现在配备了对 C、C++、Python 和 Android 的编程接口。OpenCV 在 BSD 许可下发布,因此它被用于学术项目和商业产品。
OpenCV 2.4 现在配备了全新的 FaceRecognizer 类,用于人脸识别,因此您可以立即开始进行人脸识别的实验。这份文档是我自己深入学习人脸识别时希望得到的指南。它向您展示如何在 OpenCV 中使用 FaceRecognizer 进行人脸识别(包含完整的源代码清单),并介绍了背后的算法。我还将展示如何创建您在许多出版物中看到的可视化效果,因为许多人要求这样做。
当前可用的算法是
您无需从本页复制粘贴源代码示例,因为它们位于随附此文档的 src 文件夹中。如果您使用打开的样本构建了 OpenCV,那么很有可能您已经将它们编译好了!虽然对于非常高级的用户来说,这可能很有趣,但我决定不提供实现细节,因为我担心它们会让新用户感到困惑。
本文档中的所有代码均在 BSD 许可 下发布,因此您可以随意将其用于您的项目。
人脸识别对人类来说是一项简单的任务。在 [274] 中的实验表明,即使是一到三天的婴儿也能够区分已知的面孔。那么对计算机来说有多难呢?事实证明,我们对目前的人类识别知之甚少。我们使用内在特征(眼睛、鼻子、嘴巴)还是外在特征(头部形状、发际线)来进行成功的人脸识别?我们如何分析图像,以及大脑如何对其进行编码?David Hubel 和 Torsten Wiesel 证明了我们的大脑具有专门的神经细胞,可以响应场景的特定局部特征,例如线条、边缘、角度或运动。由于我们不是将世界视为分散的碎片,所以我们的视觉皮层必须以某种方式将不同的信息来源组合成有用的模式。自动人脸识别就是从图像中提取这些有意义的特征,将它们转换成有用的表示形式,并对它们执行某种分类。
基于人脸几何特征的人脸识别可能是人脸识别最直观的做法。最早的自动人脸识别系统之一是在 [142] 中描述的:使用标记点(眼睛、耳朵、鼻子等的位置)来构建特征向量(点之间的距离、它们之间的角度等)。识别是通过计算探测图像和参考图像的特征向量之间的欧几里得距离来完成的。这种方法本质上对光照变化具有鲁棒性,但有一个很大的缺点:即使使用最先进的算法,标记点的精确配准也很复杂。在 [43] 中,对几何人脸识别进行了最新的研究。使用了 22 维特征向量,并且对大型数据集的实验表明,仅几何特征可能不足以进行人脸识别。
在 [275] 中描述的特征脸方法采用了一种整体的人脸识别方法:人脸图像是一个来自高维图像空间的点,并找到一个低维表示,在该表示中,分类变得容易。使用主成分分析找到低维子空间,该子空间识别出方差最大的轴。虽然这种类型的变换从重建角度来看是最佳的,但它没有考虑任何类别标签。想象一下,方差来自外部来源,例如光线。方差最大的轴不一定包含任何判别信息,因此分类变得不可能。因此,在 [23] 中将特定于类别的投影与线性判别分析应用于人脸识别。基本思想是在最小化类内方差的同时,最大化类间方差。
最近,出现了各种用于局部特征提取的方法。为了避免输入数据的维数过高,只描述图像的局部区域,提取的特征(希望)对局部遮挡、光照和样本大小的变化更加鲁棒。用于局部特征提取的算法包括 Gabor 小波 ([298])、离散余弦变换 ([189]) 和局部二值模式 ([3])。在应用局部特征提取时,如何最好地保留空间信息仍然是一个开放的研究问题,因为空间信息是潜在的有用信息。
让我们先获取一些数据来进行实验。我不想在这里做玩具示例。我们正在进行人脸识别,所以您需要一些人脸图像!您可以创建自己的数据集,也可以从可用的人脸数据库之一开始,http://face-rec.org/databases/ 提供了最新的概述。三个有趣的数据集是(部分描述摘自 http://face-rec.org)
耶鲁人脸数据库 A,也称为耶鲁人脸。AT&T 人脸数据库适合初始测试,但它是一个相当容易的数据集。特征脸方法在该数据集上的识别率已达到 97%,因此您不会在其他算法中看到任何显著的改进。耶鲁人脸数据库 A(也称为耶鲁人脸)是一个更适合初始实验的数据集,因为识别问题更难。该数据库包含 15 个人(14 个男性,1 个女性),每个人都有 11 张大小为 \(320 \times 243\) 像素的灰度图像。光照条件(中心光、左光、右光)、面部表情(开心、正常、悲伤、困倦、惊讶、眨眼)和眼镜(戴眼镜、不戴眼镜)有所变化。
原始图像未裁剪且未对齐。请查看 附录,了解用于完成此任务的 Python 脚本。
一旦我们获取了一些数据,就需要将其读入我们的程序。在演示应用程序中,我决定从一个非常简单的 CSV 文件中读取图像。为什么?因为我认为这是最简单的平台无关的方法。但是,如果您知道更简单的解决方案,请告诉我。基本上,CSV 文件只需要包含由文件名后跟分号(;)和标签(作为整数)组成的行,形成以下形式的行:
让我们来分析一下这条线。/path/to/image.ext 是图像的路径,如果您在 Windows 中,可能类似于:C:/faces/person0/image0.jpg。然后是分隔符 ;,最后我们为图像分配标签 0。将标签视为图像所属的个体(人),因此同一个体(人)应该具有相同的标签。
从 AT&T 人脸数据库下载 AT&T 人脸数据库,并从 at.txt 下载相应的 CSV 文件,它看起来像这样(文件当然不包含 ...)
假设我已经将文件提取到 D:/data/at,并将 CSV 文件下载到 D:/data/at.txt。那么您只需要搜索并替换 ./ 为 D:/data/。您可以在您选择的编辑器中执行此操作,每个功能足够强大的编辑器都可以做到这一点。一旦您拥有包含有效文件名和标签的 CSV 文件,就可以通过将 CSV 文件的路径作为参数传递来运行任何演示
请参阅 创建 CSV 文件,了解有关创建 CSV 文件的详细信息。
我们给出的图像表示问题在于其高维性。二维 \(p \times q\) 灰度图像跨越 \(m = pq\) 维向量空间,因此具有 \(100 \times 100\) 像素的图像已经位于 \(10,000\) 维图像空间中。问题是:所有维度对我们来说都同样有用吗?我们只有在数据存在差异的情况下才能做出决定,因此我们正在寻找的是占大多数信息的成分。主成分分析 (PCA) 由 卡尔·皮尔逊 (1901) 和 哈罗德·霍特林 (1933) 独立提出,用于将一组可能相关的变量转换为一组较小的不相关变量。其思想是,高维数据集通常由相关变量描述,因此只有几个有意义的维度占大多数信息。PCA 方法找到数据中方差最大的方向,称为主成分。
令 \(X = \{ x_{1}, x_{2}, \ldots, x_{n} \}\) 为具有观测值 \(x_i \in R^{d}\) 的随机向量。
计算均值 \(\mu\)
\[\mu = \frac{1}{n} \sum_{i=1}^{n} x_{i}\]
计算协方差矩阵 S
\[S = \frac{1}{n} \sum_{i=1}^{n} (x_{i} - \mu) (x_{i} - \mu)^{T}`\]
计算 \(S\) 的特征值 \(\lambda_{i}\) 和特征向量 \(v_{i}\)
\[S v_{i} = \lambda_{i} v_{i}, i=1,2,\ldots,n\]
则观测向量 \(x\) 的前 \(k\) 个主成分为
\[y = W^{T} (x - \mu)\]
其中 \(W = (v_{1}, v_{2}, \ldots, v_{k})\)。
从 PCA 基进行重建由以下给出
\[x = W y + \mu\]
其中 \(W = (v_{1}, v_{2}, \ldots, v_{k})\)。
然后,特征脸方法通过以下方式执行人脸识别:
仍然有一个问题需要解决。假设我们给出了 \(400\) 张大小为 \(100 \times 100\) 像素的图像。主成分分析求解协方差矩阵 \(S = X X^{T}\),其中在我们的示例中 \({size}(X) = 10000 \times 400\)。最终将得到一个 \(10000 \times 10000\) 矩阵,大约 \(0.8 GB\)。解决此问题不可行,因此我们需要应用一个技巧。从你的线性代数课程中你了解到,一个 \(M \times N\) 矩阵,其中 \(M > N\),最多只有 \(N - 1\) 个非零特征值。因此,可以采用大小为 \(N \times N\) 的特征值分解 \(S = X^{T} X\)
\[X^{T} X v_{i} = \lambda_{i} v{i}\]
并通过左乘数据矩阵获得 \(S = X X^{T}\) 的原始特征向量
\[X X^{T} (X v_{i}) = \lambda_{i} (X v_{i})\]
得到的特征向量是正交的,为了得到正交的特征向量,需要将它们归一化到单位长度。我不想把它变成一篇出版物,所以请查阅 [75] 了解方程的推导和证明。
对于第一个源代码示例,我将与你一起逐步进行。我首先提供给你完整的源代码清单,之后我们将详细查看最重要的行。请注意:每个源代码清单都进行了详细注释,因此你应该能够轻松地理解它。
此演示应用程序的源代码也包含在本文档附带的 src 文件夹中
我使用了喷气色图,所以你可以看到灰度值在特定特征脸中的分布方式。你可以看到,特征脸不仅编码了面部特征,还编码了图像中的光照(参见特征脸 #4 中的左侧光,特征脸 #5 中的右侧光)

我们已经看到,我们可以从其低维近似中重建一张脸。那么,让我们看看需要多少个特征脸才能实现良好的重建。我将做一个 \(10,30,\ldots,310\) 个特征脸的子图
10 个特征向量显然不足以实现良好的图像重建,50 个特征向量可能已经足以编码重要的面部特征。对于 AT&T 面部数据库,使用大约 300 个特征向量可以获得良好的重建。关于在成功的面部识别中应该选择多少个特征脸存在一些经验法则,但这在很大程度上取决于输入数据。 [319] 是开始研究这方面的完美起点

主成分分析 (PCA) 是特征脸方法的核心,它找到一个特征的线性组合,以最大化数据中的总方差。虽然这显然是一种强大的数据表示方法,但它不考虑任何类,因此在丢弃组件时,可能会丢失大量判别信息。想象一下,数据中的方差是由外部来源产生的,例如光照。PCA 识别的组件不一定包含任何判别信息,因此投影样本会一起模糊,分类变得不可能(请参阅 http://www.bytefish.de/wiki/pca_lda_with_gnu_octave 获取示例)。
线性判别分析 (LDA) 执行特定于类的降维,由伟大的统计学家 Sir R. A. Fisher 发明。他在 1936 年的论文 *The use of multiple measurements in taxonomic problems* [91] 中成功地将其用于对花卉进行分类。为了找到最能区分类之间的特征组合,线性判别分析最大化类间散布与类内散布的比率,而不是最大化总散布。这个想法很简单:相同的类应该紧密地聚集在一起,而不同的类在低维表示中应该尽可能地远离彼此。这一点也得到了 Belhumeur、Hespanha 和 Kriegman 的认可,因此他们在 [23] 中将判别分析应用于面部识别。
令 \(X\) 为一个随机向量,其样本来自 \(c\) 个类
\[\begin{align*} X & = & \{X_1,X_2,\ldots,X_c\} \\ X_i & = & \{x_1, x_2, \ldots, x_n\} \end{align*}\]
计算散布矩阵 \(S_{B}\) 和 S_{W} 为
\[\begin{align*} S_{B} & = & \sum_{i=1}^{c} N_{i} (\mu_i - \mu)(\mu_i - \mu)^{T} \\ S_{W} & = & \sum_{i=1}^{c} \sum_{x_{j} \in X_{i}} (x_j - \mu_i)(x_j - \mu_i)^{T} \end{align*}\]
, 其中 \(\mu\) 是总平均值
\[\mu = \frac{1}{N} \sum_{i=1}^{N} x_i\]
而 \(\mu_i\) 是类 \(i \in \{1,\ldots,c\}\) 的平均值
\[\mu_i = \frac{1}{|X_i|} \sum_{x_j \in X_i} x_j\]
Fisher 的经典算法现在寻找一个投影 \(W\),该投影最大化类可分离性标准
\[W_{opt} = \operatorname{arg\,max}_{W} \frac{|W^T S_B W|}{|W^T S_W W|}\]
遵循 [23],此优化问题的解是通过求解广义特征值问题得到的
\[\begin{align*} S_{B} v_{i} & = & \lambda_{i} S_w v_{i} \nonumber \\ S_{W}^{-1} S_{B} v_{i} & = & \lambda_{i} v_{i} \end{align*}\]
还有一个问题需要解决:\(S_{W}\) 的秩最多为 \((N-c)\),其中 \(N\) 为样本数,\(c\) 为类别数。在模式识别问题中,样本数 \(N\) 几乎总是小于输入数据的维数(像素数),因此散射矩阵 \(S_{W}\) 会变成奇异矩阵(参见 [222])。在 [23] 中,这个问题通过对数据进行主成分分析并将样本投影到 \((N-c)\) 维空间来解决。然后对降维后的数据执行线性判别分析,因为 \(S_{W}\) 不再是奇异矩阵。
然后,优化问题可以改写为
\[\begin{align*} W_{pca} & = & \operatorname{arg\,max}_{W} |W^T S_T W| \\ W_{fld} & = & \operatorname{arg\,max}_{W} \frac{|W^T W_{pca}^T S_{B} W_{pca} W|}{|W^T W_{pca}^T S_{W} W_{pca} W|} \end{align*}\]
将样本投影到 \((c-1)\) 维空间的变换矩阵 \(W\) 为
\[W = W_{fld}^{T} W_{pca}^{T}\]
此演示应用程序的源代码也包含在本文档附带的 src 文件夹中
对于这个例子,我将使用耶鲁人脸数据库 A,因为它的图形更漂亮。每个 Fisherface 的长度与原始图像相同,因此可以以图像的形式显示。演示展示(或保存)了第一个(最多 16 个)Fisherfaces

Fisherfaces 方法学习了一个特定于类别的变换矩阵,因此它们不像 Eigenfaces 方法那样明显地捕获光照。相反,判别分析找到了用于区分人物的面部特征。重要的是要提一下,Fisherfaces 的性能在很大程度上取决于输入数据。实际上,如果只用光照良好的图片学习 Fisherfaces,然后尝试识别光照不良场景中的面部,则该方法很可能找到错误的成分(因为这些特征在光照不良的图像上可能不突出)。这是有一定道理的,因为该方法没有机会学习光照。
Fisherfaces 允许重建投影后的图像,就像 Eigenfaces 一样。但是,由于我们只识别了用于区分个体的特征,因此不能期望对原始图像进行良好的重建。对于 Fisherfaces 方法,我们将样本图像投影到每个 Fisherface 上。因此,你将获得一个很好的可视化效果,它描述了每个 Fisherface 的特征
人眼可能无法察觉细微的差异,但你应该能够看到一些差异

Eigenfaces 和 Fisherfaces 对人脸识别采用了某种整体方法。你将你的数据视为高维图像空间中的某个向量。我们都知道高维性不好,因此识别出一个低维子空间,其中(可能)保留了有用信息。Eigenfaces 方法最大化了总散布,如果方差是由外部来源产生的,这可能会导致问题,因为所有类别上的最大方差的成分不一定对分类有用(参见 http://www.bytefish.de/wiki/pca_lda_with_gnu_octave)。为了保留一些判别信息,我们应用了线性判别分析,并如 Fisherfaces 方法中所述进行优化。Fisherfaces 方法运行良好...... 至少在我们模型中假设的受限场景下是这样。
现实生活并不完美。你无法保证图像的光线设置完美,也无法保证每个人都有 10 张不同的图像。那么,如果每个人只有一张图像怎么办?我们对子空间的协方差估计可能非常错误,因此识别结果也会很差。还记得 Eigenfaces 方法在 AT&T 人脸数据库上获得了 96% 的识别率吗?实际上,我们需要多少张图像才能获得如此有用的估计?以下是 Eigenfaces 和 Fisherfaces 方法在 AT&T 人脸数据库上的 Rank-1 识别率,该数据库是一个相当容易的图像数据库
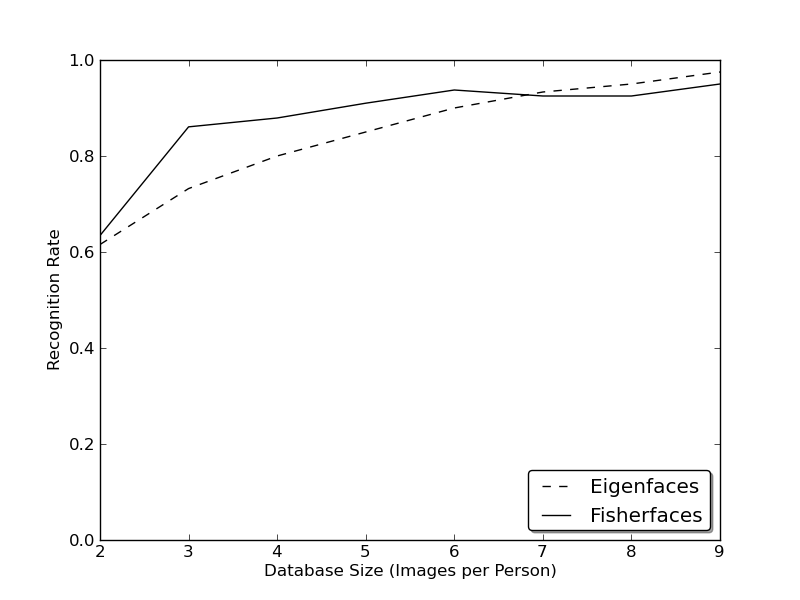
因此,为了获得良好的识别率,你需要为每个人至少准备 8 张(+-1 张)图像,而 Fisherfaces 方法在这里并没有真正帮助。以上实验是在 facerec 框架中进行的 10 折交叉验证结果,该框架位于:https://github.com/bytefish/facerec。这不是一篇出版物,因此我不会用深入的数学分析来支持这些数据。请参阅 [183],以详细了解这两种方法在小型训练数据集中的表现。
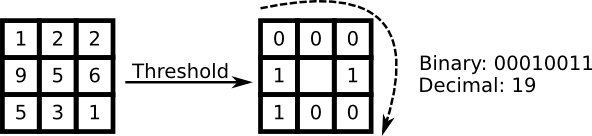
因此,一些研究集中在从图像中提取局部特征。其理念是不将整个图像视为高维向量,而是只描述对象的局部特征。这样提取的特征将隐式地具有低维性。好主意!但你很快就会发现,我们给定的图像表示不仅受光照变化的影响。想想图像中的尺度、平移或旋转等问题 - 你的局部描述至少应该对这些问题有些鲁棒性。就像 SIFT 一样,局部二值模式方法起源于 2D 纹理分析。局部二值模式的基本理念是通过比较每个像素与其邻域来总结图像中的局部结构。将一个像素作为中心,并将其邻居与阈值进行比较。如果中心像素的强度大于或等于其邻居,则用 1 表示,否则用 0 表示。你将为每个像素得到一个二进制数,就像
LBP 运算符的更正式描述可以给出如下
\[LBP(x_c, y_c) = \sum_{p=0}^{P-1} 2^p s(i_p - i_c)\]
,其中 \((x_c, y_c)\) 是强度为 \(i_c\) 的中心像素;\(i_n\) 是邻居像素的强度。\(s\) 是符号函数,定义为
\[\begin{equation} s(x) = \begin{cases} 1 & \text{if \(x \geq 0\)}\\ 0 & \text{else} \end{cases} \end{equation}\]
此描述使你能够捕获图像中非常细致的细节。事实上,作者能够在纹理分类方面与最先进的结果相媲美。在该运算符发布后不久,人们注意到,固定邻域无法编码尺度不同的细节。因此,该运算符扩展到在 [3] 中使用可变邻域。其理念是在半径可变的圆上对任意数量的邻居进行对齐,这使得能够捕获以下邻域
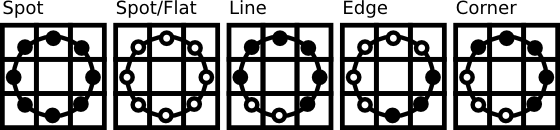
对于给定的点 \((x_c,y_c)\),邻居 \((x_p,y_p), p \in P\) 的位置可以按以下方式计算
\[\begin{align*} x_{p} & = & x_c + R \cos({\frac{2\pi p}{P}})\\ y_{p} & = & y_c - R \sin({\frac{2\pi p}{P}}) \end{align*}\]
其中 \(R\) 是圆的半径,\(P\) 是采样点数。
该运算符是对原始 LBP 代码的扩展,因此有时被称为扩展 LBP(也称为循环 LBP)。如果圆上一个点的坐标不对应于图像坐标,则该点将进行插值。计算机科学中有很多巧妙的插值方案,OpenCV 实现执行了双线性插值
\[\begin{align*} f(x,y) \approx \begin{bmatrix} 1-x & x \end{bmatrix} \begin{bmatrix} f(0,0) & f(0,1) \\ f(1,0) & f(1,1) \end{bmatrix} \begin{bmatrix} 1-y \\ y \end{bmatrix}. \end{align*}\]
根据定义,LBP 运算符对单调灰度变换具有鲁棒性。我们可以通过观察人工修改后的图像的 LBP 图像来轻松验证这一点(这样你就可以看到 LBP 图像是什么样子!)。

那么,剩下的问题是如何将空间信息合并到人脸识别模型中。Ahonen 等人提出的表示方法 [3] 是将 LBP 图像划分为 \(m\) 个局部区域,并从每个区域提取直方图。然后,通过连接这些局部直方图(而不是将它们合并)获得空间增强的特征向量。这些直方图称为局部二值模式直方图。
此演示应用程序的源代码也包含在本文档附带的 src 文件夹中
您已经了解了如何在实际应用中使用新的 FaceRecognizer。在阅读本文档后,您还了解了这些算法的工作原理,因此现在是您尝试使用可用算法的时候了。使用它们,改进它们,并让 OpenCV 社区参与进来!
如果没有获得使用AT&T 人脸数据库和耶鲁人脸数据库 A/B中人脸图像的许可,本文档将无法完成。
重要提示:使用这些图像时,请注明“AT&T 实验室,剑桥”。
人脸数据库,以前称为ORL 人脸数据库,包含一组在 1992 年 4 月至 1994 年 4 月之间拍摄的人脸图像。该数据库是在与剑桥大学工程系语音、视觉和机器人小组合作进行的人脸识别项目背景下使用的。
40 个不同主体中有 10 张不同的图像。对于某些主体,图像是在不同时间拍摄的,照明、面部表情(睁眼/闭眼、微笑/不微笑)和面部细节(戴眼镜/不戴眼镜)各不相同。所有图像均在暗色均匀背景下拍摄,主体处于直立的正面位置(允许一些侧向移动)。
这些文件采用 PGM 格式。每个图像的大小为 92x112 像素,每个像素有 256 个灰度级。图像被组织在 40 个目录中(每个目录对应一个主体),目录名称格式为 sX,其中 X 表示主体编号(介于 1 和 40 之间)。在每个目录中,该主体有 10 张不同的图像,名称格式为 Y.pgm,其中 Y 表示该主体的图像编号(介于 1 和 10 之间)。
可以在以下位置获取数据库副本:http://www.cl.cam.ac.uk/research/dtg/attarchive/pub/data/att_faces.zip.
在作者的许可下,我被允许显示少量图像(例如主体 1 和所有变化)以及来自耶鲁人脸数据库 A 或耶鲁人脸数据库 B 的所有图像,例如 Fisherfaces 和 Eigenfaces。
耶鲁人脸数据库 A(大小 6.4MB)包含 15 个个体的 165 张 GIF 格式的灰度图像。每个主体有 11 张图像,每种不同的面部表情或配置对应一张:中心光、戴眼镜、开心、左光、不戴眼镜、正常、右光、悲伤、困倦、惊讶和眨眼。(来源:http://cvc.yale.edu/projects/yalefaces/yalefaces.html)
在作者的许可下,我被允许显示少量图像(例如主体 1 和所有变化)以及来自耶鲁人脸数据库 A 或耶鲁人脸数据库 B 的所有图像,例如 Fisherfaces 和 Eigenfaces。
扩展的耶鲁人脸数据库 B 包含 28 个人类主体在 9 种姿势和 64 种照明条件下的 16128 张图像。该数据库的数据格式与耶鲁人脸数据库 B 相同。有关数据格式的更详细的信息,请参考耶鲁人脸数据库 B 的主页(或此页面的副本)。
您可以自由地将扩展的耶鲁人脸数据库 B 用于研究目的。所有使用此数据库的出版物都应确认“扩展的耶鲁人脸数据库 B”的使用,并引用 Athinodoros Georghiades、Peter Belhumeur 和 David Kriegman 的论文“From Few to Many: Illumination Cone Models for Face Recognition under Variable Lighting and Pose”,PAMI,2001,[bibtex].
扩展的数据库与最初的包含 10 个主体的耶鲁人脸数据库 B 相比,首次由 Kuang-Chih Lee、Jeffrey Ho 和 David Kriegman 在“Acquiring Linear Subspaces for Face Recognition under Variable Lighting, PAMI, May, 2005 <a href="http://vision.ucsd.edu/~leekc/papers/9pltsIEEE.pdf" target="_blank" >[pdf]</a>.” 中报道。实验中使用的所有测试图像数据均经过手动对齐、裁剪,然后重新调整大小为 168x192 的图像。如果您发布了使用裁剪后的图像的实验结果,请参考 PAMI2005 论文。(来源:http://vision.ucsd.edu/~leekc/ExtYaleDatabase/ExtYaleB.html)
您可能不想手动创建 CSV 文件。我为您准备了一个名为 create_csv.py 的小 Python 脚本(您可以在 src/create_csv.py 中找到它,该脚本随本教程提供),它会自动为您创建 CSV 文件。如果您按照以下层次结构组织图像(/basepath/<subject>/<image.ext>)
然后只需调用 create_csv.py at,其中 'at' 是指向文件夹的基路径,就像这样,您可以保存输出
以下是在您找不到该脚本的情况下提供的脚本。
#!/usr/bin/env python
import sys
import os.path
# This is a tiny script to help you creating a CSV file from a face
# database with a similar hierarchie:
#
# philipp@mango:~/facerec/data/at$ tree
# .
# |-- README
# |-- s1
# | |-- 1.pgm
# | |-- ...
# | |-- 10.pgm
# |-- s2
# | |-- 1.pgm
# | |-- ...
# | |-- 10.pgm
# ...
# |-- s40
# | |-- 1.pgm
# | |-- ...
# | |-- 10.pgm
#
if __name__ == "__main__":
if len(sys.argv) != 2:
print "usage: create_csv <base_path>"
sys.exit(1)
BASE_PATH=sys.argv[1]
SEPARATOR=";"
label = 0
for dirname, dirnames, filenames in os.walk(BASE_PATH):
for subdirname in dirnames:
subject_path = os.path.join(dirname, subdirname)
for filename in os.listdir(subject_path):
abs_path = "%s/%s" % (subject_path, filename)
print "%s%s%d" % (abs_path, SEPARATOR, label)
label = label + 1
在诸如情绪检测等任务中,对图像数据的准确对齐尤为重要,因为您需要尽可能多的细节。相信我...您不想手动执行此操作。因此我为您准备了一个小型 Python 脚本。代码使用起来非常简单。要缩放、旋转和裁剪人脸图像,您只需调用 CropFace(image, eye_left, eye_right, offset_pct, dest_sz),其中
如果您对所有图像使用相同的 offset_pct 和 dest_sz,则它们都会在眼睛处对齐。
#!/usr/bin/env python
# Software License Agreement (BSD License)
#
# Copyright (c) 2012, Philipp Wagner
# All rights reserved.
#
# Redistribution and use in source and binary forms, with or without
# modification, are permitted provided that the following conditions
# are met:
#
# * Redistributions of source code must retain the above copyright
# notice, this list of conditions and the following disclaimer.
# * Redistributions in binary form must reproduce the above
# copyright notice, this list of conditions and the following
# disclaimer in the documentation and/or other materials provided
# with the distribution.
# * Neither the name of the author nor the names of its
# contributors may be used to endorse or promote products derived
# from this software without specific prior written permission.
#
# THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS
# "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT
# LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS
# FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE
# COPYRIGHT OWNER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT,
# INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING,
# BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES;
# LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER
# CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT
# LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN
# ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE
# POSSIBILITY OF SUCH DAMAGE.
import sys, math, Image
def Distance(p1,p2):
dx = p2[0] - p1[0]
dy = p2[1] - p1[1]
return math.sqrt(dx*dx+dy*dy)
def ScaleRotateTranslate(image, angle, center = None, new_center = None, scale = None, resample=Image.BICUBIC):
if (scale is None) and (center is None):
return image.rotate(angle=angle, resample=resample)
nx,ny = x,y = center
sx=sy=1.0
if new_center:
(nx,ny) = new_center
if scale:
(sx,sy) = (scale, scale)
cosine = math.cos(angle)
sine = math.sin(angle)
a = cosine/sx
b = sine/sx
c = x-nx*a-ny*b
d = -sine/sy
e = cosine/sy
f = y-nx*d-ny*e
return image.transform(image.size, Image.AFFINE, (a,b,c,d,e,f), resample=resample)
def CropFace(image, eye_left=(0,0), eye_right=(0,0), offset_pct=(0.2,0.2), dest_sz = (70,70)):
# calculate offsets in original image
offset_h = math.floor(float(offset_pct[0])*dest_sz[0])
offset_v = math.floor(float(offset_pct[1])*dest_sz[1])
# get the direction
eye_direction = (eye_right[0] - eye_left[0], eye_right[1] - eye_left[1])
# calc rotation angle in radians
rotation = -math.atan2(float(eye_direction[1]),float(eye_direction[0]))
# distance between them
dist = Distance(eye_left, eye_right)
# calculate the reference eye-width
reference = dest_sz[0] - 2.0*offset_h
# scale factor
scale = float(dist)/float(reference)
# rotate original around the left eye
image = ScaleRotateTranslate(image, center=eye_left, angle=rotation)
# crop the rotated image
crop_xy = (eye_left[0] - scale*offset_h, eye_left[1] - scale*offset_v)
crop_size = (dest_sz[0]*scale, dest_sz[1]*scale)
image = image.crop((int(crop_xy[0]), int(crop_xy[1]), int(crop_xy[0]+crop_size[0]), int(crop_xy[1]+crop_size[1])))
# resize it
image = image.resize(dest_sz, Image.ANTIALIAS)
return image
def readFileNames():
try:
inFile = open('path_to_created_csv_file.csv')
except:
raise IOError('There is no file named path_to_created_csv_file.csv in current directory.')
return False
picPath = []
picIndex = []
for line in inFile.readlines():
if line != '':
fields = line.rstrip().split(';')
picPath.append(fields[0])
picIndex.append(int(fields[1]))
return (picPath, picIndex)
if __name__ == "__main__":
[images, indexes]=readFileNames()
if not os.path.exists("modified"):
os.makedirs("modified")
for img in images:
image = Image.open(img)
CropFace(image, eye_left=(252,364), eye_right=(420,366), offset_pct=(0.1,0.1), dest_sz=(200,200)).save("modified/"+img.rstrip().split('/')[1]+"_10_10_200_200.jpg")
CropFace(image, eye_left=(252,364), eye_right=(420,366), offset_pct=(0.2,0.2), dest_sz=(200,200)).save("modified/"+img.rstrip().split('/')[1]+"_20_20_200_200.jpg")
CropFace(image, eye_left=(252,364), eye_right=(420,366), offset_pct=(0.3,0.3), dest_sz=(200,200)).save("modified/"+img.rstrip().split('/')[1]+"_30_30_200_200.jpg")
CropFace(image, eye_left=(252,364), eye_right=(420,366), offset_pct=(0.2,0.2)).save("modified/"+img.rstrip().split('/')[1]+"_20_20_70_70.jpg")
假设我们给出了这张阿诺德·施瓦辛格的照片,它属于公共领域许可。左眼的 (x,y) 坐标大约为 *(252,364)*,右眼的坐标为 *(420,366)*。现在您只需要定义水平偏移量、垂直偏移量以及缩放、旋转和裁剪后的面部应具有的尺寸。
以下是一些示例
| 配置 | 裁剪、缩放、旋转的人脸 |
|---|---|
| 0.1 (10%), 0.1 (10%), (200,200) |  |
| 0.2 (20%), 0.2 (20%), (200,200) |  |
| 0.3 (30%), 0.3 (30%), (200,200) |  |
| 0.2 (20%), 0.2 (20%), (70,70) |  |
/home/philipp/facerec/data/at/s13/2.pgm;12 /home/philipp/facerec/data/at/s13/7.pgm;12 /home/philipp/facerec/data/at/s13/6.pgm;12 /home/philipp/facerec/data/at/s13/9.pgm;12 /home/philipp/facerec/data/at/s13/5.pgm;12 /home/philipp/facerec/data/at/s13/3.pgm;12 /home/philipp/facerec/data/at/s13/4.pgm;12 /home/philipp/facerec/data/at/s13/10.pgm;12 /home/philipp/facerec/data/at/s13/8.pgm;12 /home/philipp/facerec/data/at/s13/1.pgm;12 /home/philipp/facerec/data/at/s17/2.pgm;16 /home/philipp/facerec/data/at/s17/7.pgm;16 /home/philipp/facerec/data/at/s17/6.pgm;16 /home/philipp/facerec/data/at/s17/9.pgm;16 /home/philipp/facerec/data/at/s17/5.pgm;16 /home/philipp/facerec/data/at/s17/3.pgm;16 /home/philipp/facerec/data/at/s17/4.pgm;16 /home/philipp/facerec/data/at/s17/10.pgm;16 /home/philipp/facerec/data/at/s17/8.pgm;16 /home/philipp/facerec/data/at/s17/1.pgm;16 /home/philipp/facerec/data/at/s32/2.pgm;31 /home/philipp/facerec/data/at/s32/7.pgm;31 /home/philipp/facerec/data/at/s32/6.pgm;31 /home/philipp/facerec/data/at/s32/9.pgm;31 /home/philipp/facerec/data/at/s32/5.pgm;31 /home/philipp/facerec/data/at/s32/3.pgm;31 /home/philipp/facerec/data/at/s32/4.pgm;31 /home/philipp/facerec/data/at/s32/10.pgm;31 /home/philipp/facerec/data/at/s32/8.pgm;31 /home/philipp/facerec/data/at/s32/1.pgm;31 /home/philipp/facerec/data/at/s10/2.pgm;9 /home/philipp/facerec/data/at/s10/7.pgm;9 /home/philipp/facerec/data/at/s10/6.pgm;9 /home/philipp/facerec/data/at/s10/9.pgm;9 /home/philipp/facerec/data/at/s10/5.pgm;9 /home/philipp/facerec/data/at/s10/3.pgm;9 /home/philipp/facerec/data/at/s10/4.pgm;9 /home/philipp/facerec/data/at/s10/10.pgm;9 /home/philipp/facerec/data/at/s10/8.pgm;9 /home/philipp/facerec/data/at/s10/1.pgm;9 /home/philipp/facerec/data/at/s27/2.pgm;26 /home/philipp/facerec/data/at/s27/7.pgm;26 /home/philipp/facerec/data/at/s27/6.pgm;26 /home/philipp/facerec/data/at/s27/9.pgm;26 /home/philipp/facerec/data/at/s27/5.pgm;26 /home/philipp/facerec/data/at/s27/3.pgm;26 /home/philipp/facerec/data/at/s27/4.pgm;26 /home/philipp/facerec/data/at/s27/10.pgm;26 /home/philipp/facerec/data/at/s27/8.pgm;26 /home/philipp/facerec/data/at/s27/1.pgm;26 /home/philipp/facerec/data/at/s5/2.pgm;4 /home/philipp/facerec/data/at/s5/7.pgm;4 /home/philipp/facerec/data/at/s5/6.pgm;4 /home/philipp/facerec/data/at/s5/9.pgm;4 /home/philipp/facerec/data/at/s5/5.pgm;4 /home/philipp/facerec/data/at/s5/3.pgm;4 /home/philipp/facerec/data/at/s5/4.pgm;4 /home/philipp/facerec/data/at/s5/10.pgm;4 /home/philipp/facerec/data/at/s5/8.pgm;4 /home/philipp/facerec/data/at/s5/1.pgm;4 /home/philipp/facerec/data/at/s20/2.pgm;19 /home/philipp/facerec/data/at/s20/7.pgm;19 /home/philipp/facerec/data/at/s20/6.pgm;19 /home/philipp/facerec/data/at/s20/9.pgm;19 /home/philipp/facerec/data/at/s20/5.pgm;19 /home/philipp/facerec/data/at/s20/3.pgm;19 /home/philipp/facerec/data/at/s20/4.pgm;19 /home/philipp/facerec/data/at/s20/10.pgm;19 /home/philipp/facerec/data/at/s20/8.pgm;19 /home/philipp/facerec/data/at/s20/1.pgm;19 /home/philipp/facerec/data/at/s30/2.pgm;29 /home/philipp/facerec/data/at/s30/7.pgm;29 /home/philipp/facerec/data/at/s30/6.pgm;29 /home/philipp/facerec/data/at/s30/9.pgm;29 /home/philipp/facerec/data/at/s30/5.pgm;29 /home/philipp/facerec/data/at/s30/3.pgm;29 /home/philipp/facerec/data/at/s30/4.pgm;29 /home/philipp/facerec/data/at/s30/10.pgm;29 /home/philipp/facerec/data/at/s30/8.pgm;29 /home/philipp/facerec/data/at/s30/1.pgm;29 /home/philipp/facerec/data/at/s39/2.pgm;38 /home/philipp/facerec/data/at/s39/7.pgm;38 /home/philipp/facerec/data/at/s39/6.pgm;38 /home/philipp/facerec/data/at/s39/9.pgm;38 /home/philipp/facerec/data/at/s39/5.pgm;38 /home/philipp/facerec/data/at/s39/3.pgm;38 /home/philipp/facerec/data/at/s39/4.pgm;38 /home/philipp/facerec/data/at/s39/10.pgm;38 /home/philipp/facerec/data/at/s39/8.pgm;38 /home/philipp/facerec/data/at/s39/1.pgm;38 /home/philipp/facerec/data/at/s35/2.pgm;34 /home/philipp/facerec/data/at/s35/7.pgm;34 /home/philipp/facerec/data/at/s35/6.pgm;34 /home/philipp/facerec/data/at/s35/9.pgm;34 /home/philipp/facerec/data/at/s35/5.pgm;34 /home/philipp/facerec/data/at/s35/3.pgm;34 /home/philipp/facerec/data/at/s35/4.pgm;34 /home/philipp/facerec/data/at/s35/10.pgm;34 /home/philipp/facerec/data/at/s35/8.pgm;34 /home/philipp/facerec/data/at/s35/1.pgm;34 /home/philipp/facerec/data/at/s23/2.pgm;22 /home/philipp/facerec/data/at/s23/7.pgm;22 /home/philipp/facerec/data/at/s23/6.pgm;22 /home/philipp/facerec/data/at/s23/9.pgm;22 /home/philipp/facerec/data/at/s23/5.pgm;22 /home/philipp/facerec/data/at/s23/3.pgm;22 /home/philipp/facerec/data/at/s23/4.pgm;22 /home/philipp/facerec/data/at/s23/10.pgm;22 /home/philipp/facerec/data/at/s23/8.pgm;22 /home/philipp/facerec/data/at/s23/1.pgm;22 /home/philipp/facerec/data/at/s4/2.pgm;3 /home/philipp/facerec/data/at/s4/7.pgm;3 /home/philipp/facerec/data/at/s4/6.pgm;3 /home/philipp/facerec/data/at/s4/9.pgm;3 /home/philipp/facerec/data/at/s4/5.pgm;3 /home/philipp/facerec/data/at/s4/3.pgm;3 /home/philipp/facerec/data/at/s4/4.pgm;3 /home/philipp/facerec/data/at/s4/10.pgm;3 /home/philipp/facerec/data/at/s4/8.pgm;3 /home/philipp/facerec/data/at/s4/1.pgm;3 /home/philipp/facerec/data/at/s9/2.pgm;8 /home/philipp/facerec/data/at/s9/7.pgm;8 /home/philipp/facerec/data/at/s9/6.pgm;8 /home/philipp/facerec/data/at/s9/9.pgm;8 /home/philipp/facerec/data/at/s9/5.pgm;8 /home/philipp/facerec/data/at/s9/3.pgm;8 /home/philipp/facerec/data/at/s9/4.pgm;8 /home/philipp/facerec/data/at/s9/10.pgm;8 /home/philipp/facerec/data/at/s9/8.pgm;8 /home/philipp/facerec/data/at/s9/1.pgm;8 /home/philipp/facerec/data/at/s37/2.pgm;36 /home/philipp/facerec/data/at/s37/7.pgm;36 /home/philipp/facerec/data/at/s37/6.pgm;36 /home/philipp/facerec/data/at/s37/9.pgm;36 /home/philipp/facerec/data/at/s37/5.pgm;36 /home/philipp/facerec/data/at/s37/3.pgm;36 /home/philipp/facerec/data/at/s37/4.pgm;36 /home/philipp/facerec/data/at/s37/10.pgm;36 /home/philipp/facerec/data/at/s37/8.pgm;36 /home/philipp/facerec/data/at/s37/1.pgm;36 /home/philipp/facerec/data/at/s24/2.pgm;23 /home/philipp/facerec/data/at/s24/7.pgm;23 /home/philipp/facerec/data/at/s24/6.pgm;23 /home/philipp/facerec/data/at/s24/9.pgm;23 /home/philipp/facerec/data/at/s24/5.pgm;23 /home/philipp/facerec/data/at/s24/3.pgm;23 /home/philipp/facerec/data/at/s24/4.pgm;23 /home/philipp/facerec/data/at/s24/10.pgm;23 /home/philipp/facerec/data/at/s24/8.pgm;23 /home/philipp/facerec/data/at/s24/1.pgm;23 /home/philipp/facerec/data/at/s19/2.pgm;18 /home/philipp/facerec/data/at/s19/7.pgm;18 /home/philipp/facerec/data/at/s19/6.pgm;18 /home/philipp/facerec/data/at/s19/9.pgm;18 /home/philipp/facerec/data/at/s19/5.pgm;18 /home/philipp/facerec/data/at/s19/3.pgm;18 /home/philipp/facerec/data/at/s19/4.pgm;18 /home/philipp/facerec/data/at/s19/10.pgm;18 /home/philipp/facerec/data/at/s19/8.pgm;18 /home/philipp/facerec/data/at/s19/1.pgm;18 /home/philipp/facerec/data/at/s8/2.pgm;7 /home/philipp/facerec/data/at/s8/7.pgm;7 /home/philipp/facerec/data/at/s8/6.pgm;7 /home/philipp/facerec/data/at/s8/9.pgm;7 /home/philipp/facerec/data/at/s8/5.pgm;7 /home/philipp/facerec/data/at/s8/3.pgm;7 /home/philipp/facerec/data/at/s8/4.pgm;7 /home/philipp/facerec/data/at/s8/10.pgm;7 /home/philipp/facerec/data/at/s8/8.pgm;7 /home/philipp/facerec/data/at/s8/1.pgm;7 /home/philipp/facerec/data/at/s21/2.pgm;20 /home/philipp/facerec/data/at/s21/7.pgm;20 /home/philipp/facerec/data/at/s21/6.pgm;20 /home/philipp/facerec/data/at/s21/9.pgm;20 /home/philipp/facerec/data/at/s21/5.pgm;20 /home/philipp/facerec/data/at/s21/3.pgm;20 /home/philipp/facerec/data/at/s21/4.pgm;20 /home/philipp/facerec/data/at/s21/10.pgm;20 /home/philipp/facerec/data/at/s21/8.pgm;20 /home/philipp/facerec/data/at/s21/1.pgm;20 /home/philipp/facerec/data/at/s1/2.pgm;0 /home/philipp/facerec/data/at/s1/7.pgm;0 /home/philipp/facerec/data/at/s1/6.pgm;0 /home/philipp/facerec/data/at/s1/9.pgm;0 /home/philipp/facerec/data/at/s1/5.pgm;0 /home/philipp/facerec/data/at/s1/3.pgm;0 /home/philipp/facerec/data/at/s1/4.pgm;0 /home/philipp/facerec/data/at/s1/10.pgm;0 /home/philipp/facerec/data/at/s1/8.pgm;0 /home/philipp/facerec/data/at/s1/1.pgm;0 /home/philipp/facerec/data/at/s7/2.pgm;6 /home/philipp/facerec/data/at/s7/7.pgm;6 /home/philipp/facerec/data/at/s7/6.pgm;6 /home/philipp/facerec/data/at/s7/9.pgm;6 /home/philipp/facerec/data/at/s7/5.pgm;6 /home/philipp/facerec/data/at/s7/3.pgm;6 /home/philipp/facerec/data/at/s7/4.pgm;6 /home/philipp/facerec/data/at/s7/10.pgm;6 /home/philipp/facerec/data/at/s7/8.pgm;6 /home/philipp/facerec/data/at/s7/1.pgm;6 /home/philipp/facerec/data/at/s16/2.pgm;15 /home/philipp/facerec/data/at/s16/7.pgm;15 /home/philipp/facerec/data/at/s16/6.pgm;15 /home/philipp/facerec/data/at/s16/9.pgm;15 /home/philipp/facerec/data/at/s16/5.pgm;15 /home/philipp/facerec/data/at/s16/3.pgm;15 /home/philipp/facerec/data/at/s16/4.pgm;15 /home/philipp/facerec/data/at/s16/10.pgm;15 /home/philipp/facerec/data/at/s16/8.pgm;15 /home/philipp/facerec/data/at/s16/1.pgm;15 /home/philipp/facerec/data/at/s36/2.pgm;35 /home/philipp/facerec/data/at/s36/7.pgm;35 /home/philipp/facerec/data/at/s36/6.pgm;35 /home/philipp/facerec/data/at/s36/9.pgm;35 /home/philipp/facerec/data/at/s36/5.pgm;35 /home/philipp/facerec/data/at/s36/3.pgm;35 /home/philipp/facerec/data/at/s36/4.pgm;35 /home/philipp/facerec/data/at/s36/10.pgm;35 /home/philipp/facerec/data/at/s36/8.pgm;35 /home/philipp/facerec/data/at/s36/1.pgm;35 /home/philipp/facerec/data/at/s25/2.pgm;24 /home/philipp/facerec/data/at/s25/7.pgm;24 /home/philipp/facerec/data/at/s25/6.pgm;24 /home/philipp/facerec/data/at/s25/9.pgm;24 /home/philipp/facerec/data/at/s25/5.pgm;24 /home/philipp/facerec/data/at/s25/3.pgm;24 /home/philipp/facerec/data/at/s25/4.pgm;24 /home/philipp/facerec/data/at/s25/10.pgm;24 /home/philipp/facerec/data/at/s25/8.pgm;24 /home/philipp/facerec/data/at/s25/1.pgm;24 /home/philipp/facerec/data/at/s14/2.pgm;13 /home/philipp/facerec/data/at/s14/7.pgm;13 /home/philipp/facerec/data/at/s14/6.pgm;13 /home/philipp/facerec/data/at/s14/9.pgm;13 /home/philipp/facerec/data/at/s14/5.pgm;13 /home/philipp/facerec/data/at/s14/3.pgm;13 /home/philipp/facerec/data/at/s14/4.pgm;13 /home/philipp/facerec/data/at/s14/10.pgm;13 /home/philipp/facerec/data/at/s14/8.pgm;13 /home/philipp/facerec/data/at/s14/1.pgm;13 /home/philipp/facerec/data/at/s34/2.pgm;33 /home/philipp/facerec/data/at/s34/7.pgm;33 /home/philipp/facerec/data/at/s34/6.pgm;33 /home/philipp/facerec/data/at/s34/9.pgm;33 /home/philipp/facerec/data/at/s34/5.pgm;33 /home/philipp/facerec/data/at/s34/3.pgm;33 /home/philipp/facerec/data/at/s34/4.pgm;33 /home/philipp/facerec/data/at/s34/10.pgm;33 /home/philipp/facerec/data/at/s34/8.pgm;33 /home/philipp/facerec/data/at/s34/1.pgm;33 /home/philipp/facerec/data/at/s11/2.pgm;10 /home/philipp/facerec/data/at/s11/7.pgm;10 /home/philipp/facerec/data/at/s11/6.pgm;10 /home/philipp/facerec/data/at/s11/9.pgm;10 /home/philipp/facerec/data/at/s11/5.pgm;10 /home/philipp/facerec/data/at/s11/3.pgm;10 /home/philipp/facerec/data/at/s11/4.pgm;10 /home/philipp/facerec/data/at/s11/10.pgm;10 /home/philipp/facerec/data/at/s11/8.pgm;10 /home/philipp/facerec/data/at/s11/1.pgm;10 /home/philipp/facerec/data/at/s26/2.pgm;25 /home/philipp/facerec/data/at/s26/7.pgm;25 /home/philipp/facerec/data/at/s26/6.pgm;25 /home/philipp/facerec/data/at/s26/9.pgm;25 /home/philipp/facerec/data/at/s26/5.pgm;25 /home/philipp/facerec/data/at/s26/3.pgm;25 /home/philipp/facerec/data/at/s26/4.pgm;25 /home/philipp/facerec/data/at/s26/10.pgm;25 /home/philipp/facerec/data/at/s26/8.pgm;25 /home/philipp/facerec/data/at/s26/1.pgm;25 /home/philipp/facerec/data/at/s18/2.pgm;17 /home/philipp/facerec/data/at/s18/7.pgm;17 /home/philipp/facerec/data/at/s18/6.pgm;17 /home/philipp/facerec/data/at/s18/9.pgm;17 /home/philipp/facerec/data/at/s18/5.pgm;17 /home/philipp/facerec/data/at/s18/3.pgm;17 /home/philipp/facerec/data/at/s18/4.pgm;17 /home/philipp/facerec/data/at/s18/10.pgm;17 /home/philipp/facerec/data/at/s18/8.pgm;17 /home/philipp/facerec/data/at/s18/1.pgm;17 /home/philipp/facerec/data/at/s29/2.pgm;28 /home/philipp/facerec/data/at/s29/7.pgm;28 /home/philipp/facerec/data/at/s29/6.pgm;28 /home/philipp/facerec/data/at/s29/9.pgm;28 /home/philipp/facerec/data/at/s29/5.pgm;28 /home/philipp/facerec/data/at/s29/3.pgm;28 /home/philipp/facerec/data/at/s29/4.pgm;28 /home/philipp/facerec/data/at/s29/10.pgm;28 /home/philipp/facerec/data/at/s29/8.pgm;28 /home/philipp/facerec/data/at/s29/1.pgm;28 /home/philipp/facerec/data/at/s33/2.pgm;32 /home/philipp/facerec/data/at/s33/7.pgm;32 /home/philipp/facerec/data/at/s33/6.pgm;32 /home/philipp/facerec/data/at/s33/9.pgm;32 /home/philipp/facerec/data/at/s33/5.pgm;32 /home/philipp/facerec/data/at/s33/3.pgm;32 /home/philipp/facerec/data/at/s33/4.pgm;32 /home/philipp/facerec/data/at/s33/10.pgm;32 /home/philipp/facerec/data/at/s33/8.pgm;32 /home/philipp/facerec/data/at/s33/1.pgm;32 /home/philipp/facerec/data/at/s12/2.pgm;11 /home/philipp/facerec/data/at/s12/7.pgm;11 /home/philipp/facerec/data/at/s12/6.pgm;11 /home/philipp/facerec/data/at/s12/9.pgm;11 /home/philipp/facerec/data/at/s12/5.pgm;11 /home/philipp/facerec/data/at/s12/3.pgm;11 /home/philipp/facerec/data/at/s12/4.pgm;11 /home/philipp/facerec/data/at/s12/10.pgm;11 /home/philipp/facerec/data/at/s12/8.pgm;11 /home/philipp/facerec/data/at/s12/1.pgm;11 /home/philipp/facerec/data/at/s6/2.pgm;5 /home/philipp/facerec/data/at/s6/7.pgm;5 /home/philipp/facerec/data/at/s6/6.pgm;5 /home/philipp/facerec/data/at/s6/9.pgm;5 /home/philipp/facerec/data/at/s6/5.pgm;5 /home/philipp/facerec/data/at/s6/3.pgm;5 /home/philipp/facerec/data/at/s6/4.pgm;5 /home/philipp/facerec/data/at/s6/10.pgm;5 /home/philipp/facerec/data/at/s6/8.pgm;5 /home/philipp/facerec/data/at/s6/1.pgm;5 /home/philipp/facerec/data/at/s22/2.pgm;21 /home/philipp/facerec/data/at/s22/7.pgm;21 /home/philipp/facerec/data/at/s22/6.pgm;21 /home/philipp/facerec/data/at/s22/9.pgm;21 /home/philipp/facerec/data/at/s22/5.pgm;21 /home/philipp/facerec/data/at/s22/3.pgm;21 /home/philipp/facerec/data/at/s22/4.pgm;21 /home/philipp/facerec/data/at/s22/10.pgm;21 /home/philipp/facerec/data/at/s22/8.pgm;21 /home/philipp/facerec/data/at/s22/1.pgm;21 /home/philipp/facerec/data/at/s15/2.pgm;14 /home/philipp/facerec/data/at/s15/7.pgm;14 /home/philipp/facerec/data/at/s15/6.pgm;14 /home/philipp/facerec/data/at/s15/9.pgm;14 /home/philipp/facerec/data/at/s15/5.pgm;14 /home/philipp/facerec/data/at/s15/3.pgm;14 /home/philipp/facerec/data/at/s15/4.pgm;14 /home/philipp/facerec/data/at/s15/10.pgm;14 /home/philipp/facerec/data/at/s15/8.pgm;14 /home/philipp/facerec/data/at/s15/1.pgm;14 /home/philipp/facerec/data/at/s2/2.pgm;1 /home/philipp/facerec/data/at/s2/7.pgm;1 /home/philipp/facerec/data/at/s2/6.pgm;1 /home/philipp/facerec/data/at/s2/9.pgm;1 /home/philipp/facerec/data/at/s2/5.pgm;1 /home/philipp/facerec/data/at/s2/3.pgm;1 /home/philipp/facerec/data/at/s2/4.pgm;1 /home/philipp/facerec/data/at/s2/10.pgm;1 /home/philipp/facerec/data/at/s2/8.pgm;1 /home/philipp/facerec/data/at/s2/1.pgm;1 /home/philipp/facerec/data/at/s31/2.pgm;30 /home/philipp/facerec/data/at/s31/7.pgm;30 /home/philipp/facerec/data/at/s31/6.pgm;30 /home/philipp/facerec/data/at/s31/9.pgm;30 /home/philipp/facerec/data/at/s31/5.pgm;30 /home/philipp/facerec/data/at/s31/3.pgm;30 /home/philipp/facerec/data/at/s31/4.pgm;30 /home/philipp/facerec/data/at/s31/10.pgm;30 /home/philipp/facerec/data/at/s31/8.pgm;30 /home/philipp/facerec/data/at/s31/1.pgm;30 /home/philipp/facerec/data/at/s28/2.pgm;27 /home/philipp/facerec/data/at/s28/7.pgm;27 /home/philipp/facerec/data/at/s28/6.pgm;27 /home/philipp/facerec/data/at/s28/9.pgm;27 /home/philipp/facerec/data/at/s28/5.pgm;27 /home/philipp/facerec/data/at/s28/3.pgm;27 /home/philipp/facerec/data/at/s28/4.pgm;27 /home/philipp/facerec/data/at/s28/10.pgm;27 /home/philipp/facerec/data/at/s28/8.pgm;27 /home/philipp/facerec/data/at/s28/1.pgm;27 /home/philipp/facerec/data/at/s40/2.pgm;39 /home/philipp/facerec/data/at/s40/7.pgm;39 /home/philipp/facerec/data/at/s40/6.pgm;39 /home/philipp/facerec/data/at/s40/9.pgm;39 /home/philipp/facerec/data/at/s40/5.pgm;39 /home/philipp/facerec/data/at/s40/3.pgm;39 /home/philipp/facerec/data/at/s40/4.pgm;39 /home/philipp/facerec/data/at/s40/10.pgm;39 /home/philipp/facerec/data/at/s40/8.pgm;39 /home/philipp/facerec/data/at/s40/1.pgm;39 /home/philipp/facerec/data/at/s3/2.pgm;2 /home/philipp/facerec/data/at/s3/7.pgm;2 /home/philipp/facerec/data/at/s3/6.pgm;2 /home/philipp/facerec/data/at/s3/9.pgm;2 /home/philipp/facerec/data/at/s3/5.pgm;2 /home/philipp/facerec/data/at/s3/3.pgm;2 /home/philipp/facerec/data/at/s3/4.pgm;2 /home/philipp/facerec/data/at/s3/10.pgm;2 /home/philipp/facerec/data/at/s3/8.pgm;2 /home/philipp/facerec/data/at/s3/1.pgm;2 /home/philipp/facerec/data/at/s38/2.pgm;37 /home/philipp/facerec/data/at/s38/7.pgm;37 /home/philipp/facerec/data/at/s38/6.pgm;37 /home/philipp/facerec/data/at/s38/9.pgm;37 /home/philipp/facerec/data/at/s38/5.pgm;37 /home/philipp/facerec/data/at/s38/3.pgm;37 /home/philipp/facerec/data/at/s38/4.pgm;37 /home/philipp/facerec/data/at/s38/10.pgm;37 /home/philipp/facerec/data/at/s38/8.pgm;37 /home/philipp/facerec/data/at/s38/1.pgm;37
 1.9.8
1.9.8