摄像头标定与三维重建

主题
	鱼眼相机模型

详细描述

本节中的函数使用所谓的针孔相机模型。场景的视图是通过使用透视变换将场景的三维点 \(P_w\) 投影到图像平面上以形成对应的像素 \(p\) 来获得的。\(P_w\) 和 \(p\) 都分别以齐次坐标表示，即作为三维和二维齐次向量。您将在本节介绍的末尾找到射影几何、齐次向量和齐次变换的简要介绍。为了更简洁的符号，我们通常省略“齐次”，而直接说向量而不是齐次向量。

针孔相机模型给出的无畸变透视变换如下所示。

\[s \; p = A \begin{bmatrix} R|t \end{bmatrix} P_w,\]

其中 \(P_w\) 是相对于世界坐标系表示的三维点，\(p\) 是图像平面中的二维像素，\(A\) 是相机内参矩阵，\(R\) 和 \(t\) 是描述从世界坐标系到相机坐标系（或相机帧）坐标变化的旋转和平移，\(s\) 是透视变换的任意尺度因子，不属于相机模型。

相机内参矩阵 \(A\)（符号使用如 [321] 中所示，通常也表示为 \(K\)）将以相机坐标系表示的三维点投影到二维像素坐标，即

\[p = A P_c.\]

相机内参矩阵 \(A\) 由以像素单位表示的焦距 \(f_x\) 和 \(f_y\)，以及通常靠近图像中心的主点 \((c_x, c_y)\) 组成

\[A = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1},\]

因此

\[s \vecthree{u}{v}{1} = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1} \vecthree{X_c}{Y_c}{Z_c}.\]

内参矩阵不依赖于所查看的场景。因此，一旦估算出来，只要焦距固定（在使用变焦镜头的情况下），就可以重复使用。因此，如果相机的图像被缩放了一个因子，所有这些参数都需要按相同的因子进行缩放（分别乘以/除以）。

联合旋转-平移矩阵 \([R|t]\) 是透视变换和齐次变换的矩阵乘积。3x4的透视变换将相机坐标系中表示的三维点映射到图像平面中的二维点，并以归一化相机坐标 \(x' = X_c / Z_c\) 和 \(y' = Y_c / Z_c\) 表示

\[Z_c \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \end{bmatrix}.\]

齐次变换由外参 \(R\) 和 \(t\) 编码，并表示从世界坐标系 \(w\) 到相机坐标系 \(c\) 的基变换。因此，给定点 \(P\) 在世界坐标系中的表示 \(P_w\)，我们通过以下方式获得 \(P\) 在相机坐标系中的表示 \(P_c\)

\[P_c = \begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix} P_w,\]

这个齐次变换由一个3x3的旋转矩阵 \(R\) 和一个3x1的平移向量 \(t\) 组成

\[\begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix}, \]

因此

\[\begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \end{bmatrix} = \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix}.\]

结合透视变换和齐次变换，我们得到了将世界坐标系中的三维点映射到图像平面中并以归一化相机坐标表示的二维点的透视变换

\[Z_c \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} R|t \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix} = \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix},\]

其中 \(x' = X_c / Z_c\) 和 \(y' = Y_c / Z_c\)。将内参和外参的方程放在一起，我们可以将 \(s \; p = A \begin{bmatrix} R|t \end{bmatrix} P_w\) 写成

\[s \vecthree{u}{v}{1} = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1} \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix}.\]

如果 \(Z_c \ne 0\)，上述变换等价于以下形式，

\[\begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} f_x X_c/Z_c + c_x \\ f_y Y_c/Z_c + c_y \end{bmatrix}\]

其中

\[\vecthree{X_c}{Y_c}{Z_c} = \begin{bmatrix} R|t \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix}.\]

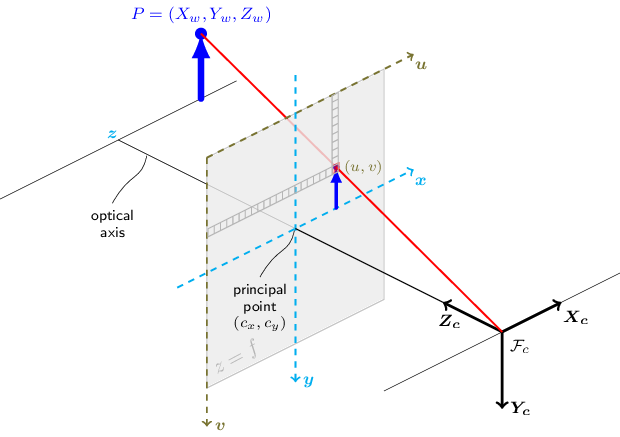
下图展示了针孔相机模型。

针孔相机模型

真实镜头通常存在一些畸变，主要是径向畸变和轻微的切向畸变。因此，上述模型被扩展为

\[\begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} f_x x'' + c_x \\ f_y y'' + c_y \end{bmatrix}\]

其中

\[\begin{bmatrix} x'' \\ y'' \end{bmatrix} = \begin{bmatrix} x' \frac{1 + k_1 r^2 + k_2 r^4 + k_3 r^6}{1 + k_4 r^2 + k_5 r^4 + k_6 r^6} + 2 p_1 x' y' + p_2(r^2 + 2 x'^2) + s_1 r^2 + s_2 r^4 \\ y' \frac{1 + k_1 r^2 + k_2 r^4 + k_3 r^6}{1 + k_4 r^2 + k_5 r^4 + k_6 r^6} + p_1 (r^2 + 2 y'^2) + 2 p_2 x' y' + s_3 r^2 + s_4 r^4 \\ \end{bmatrix}\]

其中

\[r^2 = x'^2 + y'^2\]

且

\[\begin{bmatrix} x'\\ y' \end{bmatrix} = \begin{bmatrix} X_c/Z_c \\ Y_c/Z_c \end{bmatrix},\]

如果 \(Z_c \ne 0\)。

畸变参数包括径向系数 \(k_1\)、\(k_2\)、\(k_3\)、\(k_4\)、\(k_5\) 和 \(k_6\)，\(p_1\) 和 \(p_2\) 是切向畸变系数，\(s_1\)、\(s_2\)、\(s_3\) 和 \(s_4\) 是薄棱镜畸变系数。OpenCV 中不考虑更高阶系数。

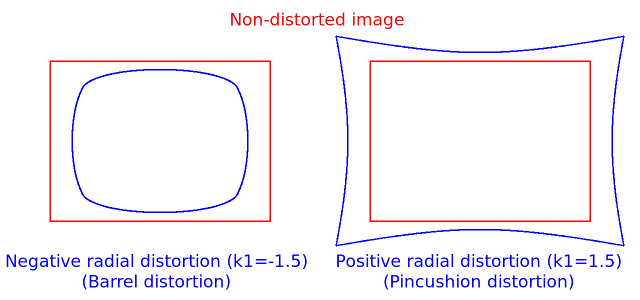
以下图片显示了两种常见的径向畸变类型：桶形畸变（\( 1 + k_1 r^2 + k_2 r^4 + k_3 r^6 \) 单调递减）和枕形畸变（\( 1 + k_1 r^2 + k_2 r^4 + k_3 r^6 \) 单调递增）。真实镜头的径向畸变总是单调的，如果估计器产生非单调结果，则应视为标定失败。更一般地，径向畸变必须是单调的，并且畸变函数必须是双射的。失败的估计结果在图像中心附近可能看起来很好，但在例如 AR/SFM 应用中会表现不佳。OpenCV 相机标定中使用的优化方法不包含这些约束，因为该框架不支持所需的整数规划和多项式不等式。有关更多信息，请参阅 issue #15992。

在某些情况下，图像传感器可能会倾斜，以便聚焦相机前方的斜平面（谢姆普鲁格原理）。这对于粒子图像测速（PIV）或使用激光扇形光进行三角测量很有用。倾斜导致 \(x''\) 和 \(y''\) 的透视畸变。这种畸变可以通过以下方式建模，参见例如 [174]。

\[\begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} f_x x''' + c_x \\ f_y y''' + c_y \end{bmatrix},\]

其中

\[s\vecthree{x'''}{y'''}{1} = \vecthreethree{R_{33}(\tau_x, \tau_y)}{0}{-R_{13}(\tau_x, \tau_y)} {0}{R_{33}(\tau_x, \tau_y)}{-R_{23}(\tau_x, \tau_y)} {0}{0}{1} R(\tau_x, \tau_y) \vecthree{x''}{y''}{1}\]

矩阵 \(R(\tau_x, \tau_y)\) 分别由两个角度参数为 \(\tau_x\) 和 \(\tau_y\) 的旋转定义，

\[ R(\tau_x, \tau_y) = \vecthreethree{\cos(\tau_y)}{0}{-\sin(\tau_y)}{0}{1}{0}{\sin(\tau_y)}{0}{\cos(\tau_y)} \vecthreethree{1}{0}{0}{0}{\cos(\tau_x)}{\sin(\tau_x)}{0}{-\sin(\tau_x)}{\cos(\tau_x)} = \vecthreethree{\cos(\tau_y)}{\sin(\tau_y)\sin(\tau_x)}{-\sin(\tau_y)\cos(\tau_x)} {0}{\cos(\tau_x)}{\sin(\tau_x)} {\sin(\tau_y)}{-\cos(\tau_y)\sin(\tau_x)}{\cos(\tau_y)\cos(\tau_x)}. \]

在下面的函数中，系数以

\[(k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6 [, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\]

向量的形式传递或返回。也就是说，如果向量包含四个元素，则表示 \(k_3=0\)。畸变系数不依赖于所查看的场景。因此，它们也属于相机内参。并且它们在捕获图像分辨率不变的情况下保持不变。例如，如果相机在320 x 240分辨率的图像上进行过标定，则对于来自同一相机的640 x 480图像，可以使用完全相同的畸变系数，而 \(f_x\)、\(f_y\)、\(c_x\) 和 \(c_y\) 需要进行适当的缩放。

以下函数使用上述模型执行以下操作

• 给定内参和外参，将三维点投影到图像平面上。
• 给定内参、一些三维点及其投影，计算外参。
• 从已知标定模式的多个视图中估算相机内参和外参（每个视图由多个三维-二维点对应关系描述）。
• 估算立体相机“头部”的相对位置和方向，并计算校正变换，使相机光轴平行。

齐次坐标
齐次坐标是射影几何中使用的坐标系统。它们的使用允许用有限坐标表示无穷远处的点，并且与笛卡尔坐标相比简化了公式，例如，它们的优点是仿射变换可以表示为线性齐次变换。

通过在n维笛卡尔向量 \(P\) 后附加一个1来获得齐次向量 \(P_h\)，例如对于三维笛卡尔向量，映射 \(P \rightarrow P_h\) 为

\[\begin{bmatrix} X \\ Y \\ Z \end{bmatrix} \rightarrow \begin{bmatrix} X \\ Y \\ Z \\ 1 \end{bmatrix}.\]

对于逆映射 \(P_h \rightarrow P\)，将齐次向量的所有元素除以其最后一个元素，例如对于三维齐次向量，其二维笛卡尔对应物为

\[\begin{bmatrix} X \\ Y \\ W \end{bmatrix} \rightarrow \begin{bmatrix} X / W \\ Y / W \end{bmatrix},\]

如果 \(W \ne 0\)。

由于这种映射，齐次点 \(P_h\) 的所有倍数 \(k P_h\)（对于 \(k \ne 0\)）都代表相同的点 \(P_h\)。对此属性的直观理解是，在透视变换下，\(P_h\) 的所有倍数都映射到同一点。这是针对针孔相机所做的物理观测，因为穿过相机针孔的一条光线上的所有点都投影到同一个图像点，例如，上述针孔相机模型图像中红光线上的所有点都将映射到相同的图像坐标。此属性也是针孔相机模型方程中尺度模糊 \(s\) 的来源。

如前所述，通过使用齐次坐标，我们可以将由 \(R\) 和 \(t\) 参数化的任何基变换表示为线性变换，例如从坐标系0到坐标系1的基变换变为

\[P_1 = R P_0 + t \rightarrow P_{h_1} = \begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix} P_{h_0}.\]

齐次变换，物体坐标系/相机坐标系
使用以下符号可以轻松实现基变换或从一个坐标系到另一个坐标系的三维坐标计算

\[ \mathbf{X}_c = \hspace{0.2em} {}^{c}\mathbf{T}_o \hspace{0.2em} \mathbf{X}_o \]

\[ \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \end{bmatrix} = \begin{bmatrix} {}^{c}\mathbf{R}_o & {}^{c}\mathbf{t}_o \\ 0_{1 \times 3} & 1 \end{bmatrix} \begin{bmatrix} X_o \\ Y_o \\ Z_o \\ 1 \end{bmatrix} \]

对于在物体坐标系中表示的三维点（\( \mathbf{X}_o \)），齐次变换矩阵 \( {}^{c}\mathbf{T}_o \) 允许计算相机坐标系中的相应坐标（\( \mathbf{X}_c \)）。该变换矩阵由一个3x3旋转矩阵 \( {}^{c}\mathbf{R}_o \) 和一个3x1平移向量 \( {}^{c}\mathbf{t}_o \) 组成。3x1平移向量 \( {}^{c}\mathbf{t}_o \) 是物体坐标系在相机坐标系中的位置，3x3旋转矩阵 \( {}^{c}\mathbf{R}_o \) 是物体坐标系在相机坐标系中的方向。

通过这个简单的符号，可以轻松地链接变换。例如，要计算在物体坐标系中表示的点在世界坐标系中的三维坐标，可以通过以下方式完成

\[ \mathbf{X}_w = \hspace{0.2em} {}^{w}\mathbf{T}_c \hspace{0.2em} {}^{c}\mathbf{T}_o \hspace{0.2em} \mathbf{X}_o = {}^{w}\mathbf{T}_o \hspace{0.2em} \mathbf{X}_o \]

类似地，逆变换可以通过以下方式完成

\[ \mathbf{X}_o = \hspace{0.2em} {}^{o}\mathbf{T}_c \hspace{0.2em} \mathbf{X}_c = \left( {}^{c}\mathbf{T}_o \right)^{-1} \hspace{0.2em} \mathbf{X}_c \]

齐次变换矩阵的逆矩阵是

\[ {}^{o}\mathbf{T}_c = \left( {}^{c}\mathbf{T}_o \right)^{-1} = \begin{bmatrix} {}^{c}\mathbf{R}^{\top}_o & - \hspace{0.2em} {}^{c}\mathbf{R}^{\top}_o \hspace{0.2em} {}^{c}\mathbf{t}_o \\ 0_{1 \times 3} & 1 \end{bmatrix} \]

可以注意到，3x3旋转矩阵的逆矩阵直接是其转置矩阵。

透视投影，从物体坐标系到相机坐标系

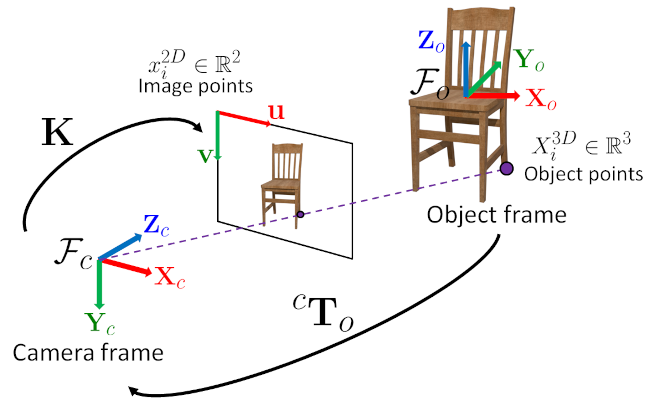
此图总结了整个过程。例如，由 solvePnP 函数或基准标记检测返回的物体姿态就是此 \( {}^{c}\mathbf{T}_o \) 变换。

相机内参矩阵 \( \mathbf{K} \) 允许将相机坐标系中表示的三维点投影到图像平面上，假设采用透视投影模型（针孔相机模型）。从经典图像处理函数中提取的图像坐标假定为 (u,v) 左上角坐标系。

注意

• 有关此主题的在线视频课程，例如
  • "3.3.1. Homogeneous Transformation Matrices", Modern Robotics, Kevin M. Lynch and Frank C. Park
• 3x3旋转矩阵由9个值组成，但描述的是3个自由度的变换
• 3x3旋转矩阵的一些附加属性是
  • \( \mathrm{det} \left( \mathbf{R} \right) = 1 \)
  • \( \mathbf{R} \mathbf{R}^{\top} = \mathbf{R}^{\top} \mathbf{R} = \mathrm{I}_{3 \times 3} \)
  • 旋转插值可以使用 Slerp（球面线性插值） 方法进行
• 不同旋转形式之间的快速转换可以使用此 在线工具 进行

从相机镜头规格推导内参
处理工业相机时，相机内参矩阵，或者更准确地说，\( \left(f_x, f_y \right) \) 可以从相机规格中推导、近似得出

\[ f_x = \frac{f_{\text{mm}}}{\text{pixel_size_in_mm}} = \frac{f_{\text{mm}}}{\text{sensor_size_in_mm} / \text{nb_pixels}} \]

同样，物理焦距可以从视角场推导出来

\[ f_{\text{mm}} = \frac{\text{sensor_size_in_mm}}{2 \times \tan{\frac{\text{fov}}{2}}} \]

后者转换在渲染软件中模仿物理相机设备时可能很有用。

注意

• 另请参见 calibrationMatrixValues

附加参考文献、注意事项

注意

• 此模块中的许多函数都将相机内参矩阵作为输入参数。尽管所有函数都假定此参数具有相同的结构，但它们可能命名不同。然而，参数的描述将清楚地表明需要具有上述结构的相机内参矩阵。
• OpenCV源代码/samples/cpp/3calibration.cpp 中可以找到3个水平放置相机的标定示例。
• OpenCV源代码/samples/cpp/calibration.cpp 中可以找到基于图像序列的标定示例。
• OpenCV源代码/samples/cpp/build3dmodel.cpp 中可以找到用于三维重建的标定示例。
• OpenCV源代码/samples/cpp/stereo_calib.cpp 中可以找到立体标定的示例。
• OpenCV源代码/samples/cpp/stereo_match.cpp 中可以找到立体匹配的示例。
• (Python) OpenCV源代码/samples/python/calibrate.py 中可以找到相机标定示例。

类
结构体	cv::CirclesGridFinderParameters
类	cv::LMSolver
类	cv::StereoBM
	用于使用块匹配算法计算立体对应关系的类，由K. Konolige引入并贡献给OpenCV。更多...
类	cv::StereoMatcher
	立体对应算法的基类。更多...
类	cv::StereoSGBM
	该类实现了修改后的H. Hirschmuller算法 [128]，它与原始算法的不同之处在于：更多...
结构体	cv::UsacParams

类型定义
typedef CirclesGridFinderParameters	cv::CirclesGridFinderParameters2

枚举
枚举	{   cv::LMEDS = 4 ,   cv::RANSAC = 8 ,   cv::RHO = 16 ,   cv::USAC_DEFAULT = 32 ,   cv::USAC_PARALLEL = 33 ,   cv::USAC_FM_8PTS = 34 ,   cv::USAC_FAST = 35 ,   cv::USAC_ACCURATE = 36 ,   cv::USAC_PROSAC = 37 ,   cv::USAC_MAGSAC = 38 }
	鲁棒估计算法的类型 更多...
枚举	{   cv::CALIB_CB_ADAPTIVE_THRESH = 1 ,   cv::CALIB_CB_NORMALIZE_IMAGE = 2 ,   cv::CALIB_CB_FILTER_QUADS = 4 ,   cv::CALIB_CB_FAST_CHECK = 8 ,   cv::CALIB_CB_EXHAUSTIVE = 16 ,   cv::CALIB_CB_ACCURACY = 32 ,   cv::CALIB_CB_LARGER = 64 ,   cv::CALIB_CB_MARKER = 128 ,   cv::CALIB_CB_PLAIN = 256 }
枚举	{   cv::CALIB_CB_SYMMETRIC_GRID = 1 ,   cv::CALIB_CB_ASYMMETRIC_GRID = 2 ,   cv::CALIB_CB_CLUSTERING = 4 }
枚举	{   cv::CALIB_NINTRINSIC = 18 ,   cv::CALIB_USE_INTRINSIC_GUESS = 0x00001 ,   cv::CALIB_FIX_ASPECT_RATIO = 0x00002 ,   cv::CALIB_FIX_PRINCIPAL_POINT = 0x00004 ,   cv::CALIB_ZERO_TANGENT_DIST = 0x00008 ,   cv::CALIB_FIX_FOCAL_LENGTH = 0x00010 ,   cv::CALIB_FIX_K1 = 0x00020 ,   cv::CALIB_FIX_K2 = 0x00040 ,   cv::CALIB_FIX_K3 = 0x00080 ,   cv::CALIB_FIX_K4 = 0x00800 ,   cv::CALIB_FIX_K5 = 0x01000 ,   cv::CALIB_FIX_K6 = 0x02000 ,   cv::CALIB_RATIONAL_MODEL = 0x04000 ,   cv::CALIB_THIN_PRISM_MODEL = 0x08000 ,   cv::CALIB_FIX_S1_S2_S3_S4 = 0x10000 ,   cv::CALIB_TILTED_MODEL = 0x40000 ,   cv::CALIB_FIX_TAUX_TAUY = 0x80000 ,   cv::CALIB_USE_QR = 0x100000 ,   cv::CALIB_FIX_TANGENT_DIST = 0x200000 ,   cv::CALIB_FIX_INTRINSIC = 0x00100 ,   cv::CALIB_SAME_FOCAL_LENGTH = 0x00200 ,   cv::CALIB_ZERO_DISPARITY = 0x00400 ,   cv::CALIB_USE_LU = (1 << 17) ,   cv::CALIB_USE_EXTRINSIC_GUESS = (1 << 22) }
枚举	{   cv::FM_7POINT = 1 ,   cv::FM_8POINT = 2 ,   cv::FM_LMEDS = 4 ,   cv::FM_RANSAC = 8 }
	寻找基础矩阵的算法 更多...
枚举	cv::HandEyeCalibrationMethod {   cv::CALIB_HAND_EYE_TSAI = 0 ,   cv::CALIB_HAND_EYE_PARK = 1 ,   cv::CALIB_HAND_EYE_HORAUD = 2 ,   cv::CALIB_HAND_EYE_ANDREFF = 3 ,   cv::CALIB_HAND_EYE_DANIILIDIS = 4 }
枚举	cv::LocalOptimMethod {   cv::LOCAL_OPTIM_NULL =0 ,   cv::LOCAL_OPTIM_INNER_LO =1 ,   cv::LOCAL_OPTIM_INNER_AND_ITER_LO =2 ,   cv::LOCAL_OPTIM_GC =3 ,   cv::LOCAL_OPTIM_SIGMA =4 }
枚举	cv::NeighborSearchMethod {   cv::NEIGH_FLANN_KNN =0 ,   cv::NEIGH_GRID =1 ,   cv::NEIGH_FLANN_RADIUS =2 }
枚举	cv::PolishingMethod {   cv::NONE_POLISHER =0 ,   cv::LSQ_POLISHER =1 ,   cv::MAGSAC =2 ,   cv::COV_POLISHER =3 }
枚举	cv::RobotWorldHandEyeCalibrationMethod {   cv::CALIB_ROBOT_WORLD_HAND_EYE_SHAH = 0 ,   cv::CALIB_ROBOT_WORLD_HAND_EYE_LI = 1 }
枚举	cv::SamplingMethod {   cv::SAMPLING_UNIFORM =0 ,   cv::SAMPLING_PROGRESSIVE_NAPSAC =1 ,   cv::SAMPLING_NAPSAC =2 ,   cv::SAMPLING_PROSAC =3 }
枚举	cv::ScoreMethod {   cv::SCORE_METHOD_RANSAC =0 ,   cv::SCORE_METHOD_MSAC =1 ,   cv::SCORE_METHOD_MAGSAC =2 ,   cv::SCORE_METHOD_LMEDS =3 }
枚举	cv::SolvePnPMethod {   cv::SOLVEPNP_ITERATIVE = 0 ,   cv::SOLVEPNP_EPNP = 1 ,   cv::SOLVEPNP_P3P = 2 ,   cv::SOLVEPNP_DLS = 3 ,   cv::SOLVEPNP_UPNP = 4 ,   cv::SOLVEPNP_AP3P = 5 ,   cv::SOLVEPNP_IPPE = 6 ,   cv::SOLVEPNP_IPPE_SQUARE = 7 ,   cv::SOLVEPNP_SQPNP = 8 }
枚举	cv::UndistortTypes {   cv::PROJ_SPHERICAL_ORTHO = 0 ,   cv::PROJ_SPHERICAL_EQRECT = 1 }
	cv::undistort 模式 更多...

函数
double	cv::calibrateCamera (InputArrayOfArrays objectPoints, InputArrayOfArrays imagePoints, Size imageSize, InputOutputArray cameraMatrix, InputOutputArray distCoeffs, OutputArrayOfArrays rvecs, OutputArrayOfArrays tvecs, int flags=0, TermCriteria criteria=TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 30, DBL_EPSILON))
double	cv::calibrateCamera (InputArrayOfArrays objectPoints, InputArrayOfArrays imagePoints, Size imageSize, InputOutputArray cameraMatrix, InputOutputArray distCoeffs, OutputArrayOfArrays rvecs, OutputArrayOfArrays tvecs, OutputArray stdDeviationsIntrinsics, OutputArray stdDeviationsExtrinsics, OutputArray perViewErrors, int flags=0, TermCriteria criteria=TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 30, DBL_EPSILON))
	从标定模式的多个视图中查找相机内参和外参。
double	cv::calibrateCameraRO (InputArrayOfArrays objectPoints, InputArrayOfArrays imagePoints, Size imageSize, int iFixedPoint, InputOutputArray cameraMatrix, InputOutputArray distCoeffs, OutputArrayOfArrays rvecs, OutputArrayOfArrays tvecs, OutputArray newObjPoints, int flags=0, TermCriteria criteria=TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 30, DBL_EPSILON))
double	cv::calibrateCameraRO (InputArrayOfArrays objectPoints, InputArrayOfArrays imagePoints, Size imageSize, int iFixedPoint, InputOutputArray cameraMatrix, InputOutputArray distCoeffs, OutputArrayOfArrays rvecs, OutputArrayOfArrays tvecs, OutputArray newObjPoints, OutputArray stdDeviationsIntrinsics, OutputArray stdDeviationsExtrinsics, OutputArray stdDeviationsObjPoints, OutputArray perViewErrors, int flags=0, TermCriteria criteria=TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 30, DBL_EPSILON))
	从标定模式的多个视图中查找相机内参和外参。
void	cv::calibrateHandEye (InputArrayOfArrays R_gripper2base, InputArrayOfArrays t_gripper2base, InputArrayOfArrays R_target2cam, InputArrayOfArrays t_target2cam, OutputArray R_cam2gripper, OutputArray t_cam2gripper, HandEyeCalibrationMethod method=CALIB_HAND_EYE_TSAI)
	计算手眼标定：\(_{}^{g}\textrm{T}_c\)。
void	cv::calibrateRobotWorldHandEye (InputArrayOfArrays R_world2cam, InputArrayOfArrays t_world2cam, InputArrayOfArrays R_base2gripper, InputArrayOfArrays t_base2gripper, OutputArray R_base2world, OutputArray t_base2world, OutputArray R_gripper2cam, OutputArray t_gripper2cam, RobotWorldHandEyeCalibrationMethod method=CALIB_ROBOT_WORLD_HAND_EYE_SHAH)
	计算机器人-世界/手眼标定：\(_{}^{w}\textrm{T}_b\) 和 \(_{}^{c}\textrm{T}_g\)。
void	cv::calibrationMatrixValues (InputArray cameraMatrix, Size imageSize, double apertureWidth, double apertureHeight, double &fovx, double &fovy, double &focalLength, Point2d &principalPoint, double &aspectRatio)
	根据相机内参矩阵计算有用的相机特性。
bool	cv::checkChessboard (InputArray img, Size size)
void	cv::composeRT (InputArray rvec1, InputArray tvec1, InputArray rvec2, InputArray tvec2, OutputArray rvec3, OutputArray tvec3, OutputArray dr3dr1=noArray(), OutputArray dr3dt1=noArray(), OutputArray dr3dr2=noArray(), OutputArray dr3dt2=noArray(), OutputArray dt3dr1=noArray(), OutputArray dt3dt1=noArray(), OutputArray dt3dr2=noArray(), OutputArray dt3dt2=noArray())
	组合两个旋转平移变换。
void	cv::computeCorrespondEpilines (InputArray points, int whichImage, InputArray F, OutputArray lines)
	对于立体对图像中的点，计算另一图像中的对应对极线。
void	cv::convertPointsFromHomogeneous (InputArray src, OutputArray dst)
	将点从齐次坐标空间转换为欧几里得空间。
void	cv::convertPointsHomogeneous (InputArray src, OutputArray dst)
	将点转换为齐次坐标或从齐次坐标转换。
void	cv::convertPointsToHomogeneous (InputArray src, OutputArray dst)
	将点从欧几里得空间转换为齐次空间。
void	cv::correctMatches (InputArray F, InputArray points1, InputArray points2, OutputArray newPoints1, OutputArray newPoints2)
	细化对应点的坐标。
void	cv::decomposeEssentialMat (InputArray E, OutputArray R1, OutputArray R2, OutputArray t)
	将本征矩阵分解为可能的旋转和平移。
int	cv::decomposeHomographyMat (InputArray H, InputArray K, OutputArrayOfArrays rotations, OutputArrayOfArrays translations, OutputArrayOfArrays normals)
	将单应性矩阵分解为旋转、平移和平面法线。
void	cv::decomposeProjectionMatrix (InputArray projMatrix, OutputArray cameraMatrix, OutputArray rotMatrix, OutputArray transVect, OutputArray rotMatrixX=noArray(), OutputArray rotMatrixY=noArray(), OutputArray rotMatrixZ=noArray(), OutputArray eulerAngles=noArray())
	将投影矩阵分解为旋转矩阵和相机内参矩阵。
void	cv::drawChessboardCorners (InputOutputArray image, Size patternSize, InputArray corners, bool patternWasFound)
	渲染检测到的棋盘角点。
void	cv::drawFrameAxes (InputOutputArray image, InputArray cameraMatrix, InputArray distCoeffs, InputArray rvec, InputArray tvec, float length, int thickness=3)
	从姿态估计中绘制世界/物体坐标系的轴。
cv::Mat	cv::estimateAffine2D (InputArray from, InputArray to, OutputArray inliers=noArray(), int method=RANSAC, double ransacReprojThreshold=3, size_t maxIters=2000, double confidence=0.99, size_t refineIters=10)
	计算两个二维点集之间的最优仿射变换。
cv::Mat	cv::estimateAffine2D (InputArray pts1, InputArray pts2, OutputArray inliers, const UsacParams &params)
cv::Mat	cv::estimateAffine3D (InputArray src, InputArray dst, double *scale=nullptr, bool force_rotation=true)
	计算两个三维点集之间的最优仿射变换。
int	cv::estimateAffine3D (InputArray src, InputArray dst, OutputArray out, OutputArray inliers, double ransacThreshold=3, double confidence=0.99)
	计算两个三维点集之间的最优仿射变换。
cv::Mat	cv::estimateAffinePartial2D (InputArray from, InputArray to, OutputArray inliers=noArray(), int method=RANSAC, double ransacReprojThreshold=3, size_t maxIters=2000, double confidence=0.99, size_t refineIters=10)
	计算两个二维点集之间具有4个自由度的最优受限仿射变换。
Scalar	cv::estimateChessboardSharpness (InputArray image, Size patternSize, InputArray corners, float rise_distance=0.8F, bool vertical=false, OutputArray sharpness=noArray())
	估计检测到的棋盘的清晰度。
int	cv::estimateTranslation3D (InputArray src, InputArray dst, OutputArray out, OutputArray inliers, double ransacThreshold=3, double confidence=0.99)
	计算两个三维点集之间的最优平移。
void	cv::filterHomographyDecompByVisibleRefpoints (InputArrayOfArrays rotations, InputArrayOfArrays normals, InputArray beforePoints, InputArray afterPoints, OutputArray possibleSolutions, InputArray pointsMask=noArray())
	根据附加信息过滤单应性分解。
void	cv::filterSpeckles (InputOutputArray img, double newVal, int maxSpeckleSize, double maxDiff, InputOutputArray buf=noArray())
	过滤视差图中小的噪声斑点。
bool	cv::find4QuadCornerSubpix (InputArray img, InputOutputArray corners, Size region_size)
	查找棋盘角点的亚像素精确位置
bool	cv::findChessboardCorners (InputArray image, Size patternSize, OutputArray corners, int flags=CALIB_CB_ADAPTIVE_THRESH+CALIB_CB_NORMALIZE_IMAGE)
	查找棋盘内部角点的位置。
bool	cv::findChessboardCornersSB (InputArray image, Size patternSize, OutputArray corners, int flags, OutputArray meta)
	使用基于扇区的方法查找棋盘内部角点的位置。
bool	cv::findChessboardCornersSB (InputArray image, Size patternSize, OutputArray corners, int flags=0)
bool	cv::findCirclesGrid (InputArray image, Size patternSize, OutputArray centers, int flags, const Ptr< FeatureDetector > &blobDetector, const CirclesGridFinderParameters &parameters)
	在圆形网格中查找中心。
bool	cv::findCirclesGrid (InputArray image, Size patternSize, OutputArray centers, int flags=CALIB_CB_SYMMETRIC_GRID, const Ptr< FeatureDetector > &blobDetector=SimpleBlobDetector::create())
Mat	cv::findEssentialMat (InputArray points1, InputArray points2, double focal, Point2d pp, int method, double prob, double threshold, OutputArray mask)
Mat	cv::findEssentialMat (InputArray points1, InputArray points2, double focal=1.0, Point2d pp=Point2d(0, 0), int method=RANSAC, double prob=0.999, double threshold=1.0, int maxIters=1000, OutputArray mask=noArray())
Mat	cv::findEssentialMat (InputArray points1, InputArray points2, InputArray cameraMatrix, int method, double prob, double threshold, OutputArray mask)
Mat	cv::findEssentialMat (InputArray points1, InputArray points2, InputArray cameraMatrix, int method=RANSAC, double prob=0.999, double threshold=1.0, int maxIters=1000, OutputArray mask=noArray())
	从两张图像中的对应点计算本征矩阵。
Mat	cv::findEssentialMat (InputArray points1, InputArray points2, InputArray cameraMatrix1, InputArray cameraMatrix2, InputArray dist_coeff1, InputArray dist_coeff2, OutputArray mask, const UsacParams &params)
Mat	cv::findEssentialMat (InputArray points1, InputArray points2, InputArray cameraMatrix1, InputArray distCoeffs1, InputArray cameraMatrix2, InputArray distCoeffs2, int method=RANSAC, double prob=0.999, double threshold=1.0, OutputArray mask=noArray())
	从两张（可能来自不同相机）图像中的对应点计算本征矩阵。
Mat	cv::findFundamentalMat (InputArray points1, InputArray points2, int method, double ransacReprojThreshold, double confidence, int maxIters, OutputArray mask=noArray())
	从两张图像中的对应点计算基础矩阵。
Mat	cv::findFundamentalMat (InputArray points1, InputArray points2, int method=FM_RANSAC, double ransacReprojThreshold=3., double confidence=0.99, OutputArray mask=noArray())
Mat	cv::findFundamentalMat (InputArray points1, InputArray points2, OutputArray mask, const UsacParams &params)
Mat	cv::findFundamentalMat (InputArray points1, InputArray points2, OutputArray mask, int method=FM_RANSAC, double ransacReprojThreshold=3., double confidence=0.99)
Mat	cv::findHomography (InputArray srcPoints, InputArray dstPoints, int method=0, double ransacReprojThreshold=3, OutputArray mask=noArray(), const int maxIters=2000, const double confidence=0.995)
	在两个平面之间查找透视变换。
Mat	cv::findHomography (InputArray srcPoints, InputArray dstPoints, OutputArray mask, const UsacParams &params)
Mat	cv::findHomography (InputArray srcPoints, InputArray dstPoints, OutputArray mask, int method=0, double ransacReprojThreshold=3)
Mat	cv::getDefaultNewCameraMatrix (InputArray cameraMatrix, Size imgsize=Size(), bool centerPrincipalPoint=false)
	返回默认的新相机矩阵。
Mat	cv::getOptimalNewCameraMatrix (InputArray cameraMatrix, InputArray distCoeffs, Size imageSize, double alpha, Size newImgSize=Size(), Rect *validPixROI=0, bool centerPrincipalPoint=false)
	根据自由缩放参数返回新的相机内参矩阵。
Rect	cv::getValidDisparityROI (Rect roi1, Rect roi2, int minDisparity, int numberOfDisparities, int blockSize)
	从校正图像的有效ROI（由 stereoRectify 返回）计算有效视差ROI
Mat	cv::initCameraMatrix2D (InputArrayOfArrays objectPoints, InputArrayOfArrays imagePoints, Size imageSize, double aspectRatio=1.0)
	从三维-二维点对应关系中找到初始相机内参矩阵。
void	cv::initInverseRectificationMap (InputArray cameraMatrix, InputArray distCoeffs, InputArray R, InputArray newCameraMatrix, const Size &size, int m1type, OutputArray map1, OutputArray map2)
	计算投影和逆校正变换图。本质上，这是 initUndistortRectifyMap 的逆操作，用于适应投影仪-相机对中投影仪（“逆相机”）的立体校正。
void	cv::initUndistortRectifyMap (InputArray cameraMatrix, InputArray distCoeffs, InputArray R, InputArray newCameraMatrix, Size size, int m1type, OutputArray map1, OutputArray map2)
	计算去畸变和校正变换图。
float	cv::initWideAngleProjMap (InputArray cameraMatrix, InputArray distCoeffs, Size imageSize, int destImageWidth, int m1type, OutputArray map1, OutputArray map2, enum UndistortTypes projType=PROJ_SPHERICAL_EQRECT, double alpha=0)
	为广角相机初始化 remap 的映射
static float	cv::initWideAngleProjMap (InputArray cameraMatrix, InputArray distCoeffs, Size imageSize, int destImageWidth, int m1type, OutputArray map1, OutputArray map2, int projType, double alpha=0)
void	cv::matMulDeriv (InputArray A, InputArray B, OutputArray dABdA, OutputArray dABdB)
	计算每个相乘矩阵的矩阵乘积偏导数。
void	cv::projectPoints (InputArray objectPoints, InputArray rvec, InputArray tvec, InputArray cameraMatrix, InputArray distCoeffs, OutputArray imagePoints, OutputArray jacobian=noArray(), double aspectRatio=0)
	将三维点投影到图像平面。
int	cv::recoverPose (InputArray E, InputArray points1, InputArray points2, InputArray cameraMatrix, OutputArray R, OutputArray t, double distanceThresh, InputOutputArray mask=noArray(), OutputArray triangulatedPoints=noArray())
int	cv::recoverPose (InputArray E, InputArray points1, InputArray points2, InputArray cameraMatrix, OutputArray R, OutputArray t, InputOutputArray mask=noArray())
	从估计的本征矩阵和两张图像中的对应点恢复相对相机旋转和平移，并进行手性检查。返回通过检查的内点数。
int	cv::recoverPose (InputArray E, InputArray points1, InputArray points2, OutputArray R, OutputArray t, double focal=1.0, Point2d pp=Point2d(0, 0), InputOutputArray mask=noArray())
int	cv::recoverPose (InputArray points1, InputArray points2, InputArray cameraMatrix1, InputArray distCoeffs1, InputArray cameraMatrix2, InputArray distCoeffs2, OutputArray E, OutputArray R, OutputArray t, int method=cv::RANSAC, double prob=0.999, double threshold=1.0, InputOutputArray mask=noArray())
	从两台不同摄像机的两张图像中对应的点恢复相对摄像机旋转和平移，并使用手性检查。返回通过检查的内点数量。
float	cv::rectify3Collinear (InputArray cameraMatrix1, InputArray distCoeffs1, InputArray cameraMatrix2, InputArray distCoeffs2, InputArray cameraMatrix3, InputArray distCoeffs3, InputArrayOfArrays imgpt1, InputArrayOfArrays imgpt3, Size imageSize, InputArray R12, InputArray T12, InputArray R13, InputArray T13, OutputArray R1, OutputArray R2, OutputArray R3, OutputArray P1, OutputArray P2, OutputArray P3, OutputArray Q, double alpha, Size newImgSize, Rect *roi1, Rect *roi2, int flags)
	计算3头摄像机的校正变换，其中所有摄像头位于同一直线上。
void	cv::reprojectImageTo3D (InputArray disparity, OutputArray _3dImage, InputArray Q, bool handleMissingValues=false, int ddepth=-1)
	将视差图像重新投影到3D空间。
void	cv::Rodrigues (InputArray src, OutputArray dst, OutputArray jacobian=noArray())
	将旋转矩阵转换为旋转向量，反之亦然。
Vec3d	cv::RQDecomp3x3 (InputArray src, OutputArray mtxR, OutputArray mtxQ, OutputArray Qx=noArray(), OutputArray Qy=noArray(), OutputArray Qz=noArray())
	计算3x3矩阵的RQ分解。
double	cv::sampsonDistance (InputArray pt1, InputArray pt2, InputArray F)
	计算两点之间的Sampson距离。
int	cv::solveP3P (InputArray objectPoints, InputArray imagePoints, InputArray cameraMatrix, InputArray distCoeffs, OutputArrayOfArrays rvecs, OutputArrayOfArrays tvecs, int flags)
	从3个3D-2D点对应关系中查找物体姿态 \( {}^{c}\mathbf{T}_o \) 。
bool	cv::solvePnP (InputArray objectPoints, InputArray imagePoints, InputArray cameraMatrix, InputArray distCoeffs, OutputArray rvec, OutputArray tvec, bool useExtrinsicGuess=false, int flags=SOLVEPNP_ITERATIVE)
	从3D-2D点对应关系中查找物体姿态 \( {}^{c}\mathbf{T}_o \)
int	cv::solvePnPGeneric (InputArray objectPoints, InputArray imagePoints, InputArray cameraMatrix, InputArray distCoeffs, OutputArrayOfArrays rvecs, OutputArrayOfArrays tvecs, bool useExtrinsicGuess=false, SolvePnPMethod flags=SOLVEPNP_ITERATIVE, InputArray rvec=noArray(), InputArray tvec=noArray(), OutputArray reprojectionError=noArray())
	从3D-2D点对应关系中查找物体姿态 \( {}^{c}\mathbf{T}_o \) 。
bool	cv::solvePnPRansac (InputArray objectPoints, InputArray imagePoints, InputArray cameraMatrix, InputArray distCoeffs, OutputArray rvec, OutputArray tvec, bool useExtrinsicGuess=false, int iterationsCount=100, float reprojectionError=8.0, double confidence=0.99, OutputArray inliers=noArray(), int flags=SOLVEPNP_ITERATIVE)
	使用RANSAC方案处理错误匹配，从3D-2D点对应关系中查找物体姿态 \( {}^{c}\mathbf{T}_o \) 。
bool	cv::solvePnPRansac (InputArray objectPoints, InputArray imagePoints, InputOutputArray cameraMatrix, InputArray distCoeffs, OutputArray rvec, OutputArray tvec, OutputArray inliers, const UsacParams &params=UsacParams())
void	cv::solvePnPRefineLM (InputArray objectPoints, InputArray imagePoints, InputArray cameraMatrix, InputArray distCoeffs, InputOutputArray rvec, InputOutputArray tvec, TermCriteria criteria=TermCriteria(TermCriteria::EPS+TermCriteria::COUNT, 20, FLT_EPSILON))
	从3D-2D点对应关系和初始解中，优化姿态（将3D点从物体坐标系转换到摄像机坐标系的平移和旋转）。
void	cv::solvePnPRefineVVS (InputArray objectPoints, InputArray imagePoints, InputArray cameraMatrix, InputArray distCoeffs, InputOutputArray rvec, InputOutputArray tvec, TermCriteria criteria=TermCriteria(TermCriteria::EPS+TermCriteria::COUNT, 20, FLT_EPSILON), double VVSlambda=1)
	从3D-2D点对应关系和初始解中，优化姿态（将3D点从物体坐标系转换到摄像机坐标系的平移和旋转）。
double	cv::stereoCalibrate (InputArrayOfArrays objectPoints, InputArrayOfArrays imagePoints1, InputArrayOfArrays imagePoints2, InputOutputArray cameraMatrix1, InputOutputArray distCoeffs1, InputOutputArray cameraMatrix2, InputOutputArray distCoeffs2, Size imageSize, InputOutputArray R, InputOutputArray T, OutputArray E, OutputArray F, OutputArray perViewErrors, int flags=CALIB_FIX_INTRINSIC, TermCriteria criteria=TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 30, 1e-6))
	这是一个重载的成员函数，为方便起见而提供。它与上述函数的区别仅在于它接受的参数。
double	cv::stereoCalibrate (InputArrayOfArrays objectPoints, InputArrayOfArrays imagePoints1, InputArrayOfArrays imagePoints2, InputOutputArray cameraMatrix1, InputOutputArray distCoeffs1, InputOutputArray cameraMatrix2, InputOutputArray distCoeffs2, Size imageSize, InputOutputArray R, InputOutputArray T, OutputArray E, OutputArray F, OutputArrayOfArrays rvecs, OutputArrayOfArrays tvecs, OutputArray perViewErrors, int flags=CALIB_FIX_INTRINSIC, TermCriteria criteria=TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 30, 1e-6))
	校准立体摄像机设置。此函数查找两个摄像机各自的内参和它们之间的外参。
double	cv::stereoCalibrate (InputArrayOfArrays objectPoints, InputArrayOfArrays imagePoints1, InputArrayOfArrays imagePoints2, InputOutputArray cameraMatrix1, InputOutputArray distCoeffs1, InputOutputArray cameraMatrix2, InputOutputArray distCoeffs2, Size imageSize, OutputArray R, OutputArray T, OutputArray E, OutputArray F, int flags=CALIB_FIX_INTRINSIC, TermCriteria criteria=TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 30, 1e-6))
	这是一个重载的成员函数，为方便起见而提供。它与上述函数的区别仅在于它接受的参数。
void	cv::stereoRectify (InputArray cameraMatrix1, InputArray distCoeffs1, InputArray cameraMatrix2, InputArray distCoeffs2, Size imageSize, InputArray R, InputArray T, OutputArray R1, OutputArray R2, OutputArray P1, OutputArray P2, OutputArray Q, int flags=CALIB_ZERO_DISPARITY, double alpha=-1, Size newImageSize=Size(), Rect *validPixROI1=0, Rect *validPixROI2=0)
	计算已校准立体摄像机每个摄像头的校正变换。
bool	cv::stereoRectifyUncalibrated (InputArray points1, InputArray points2, InputArray F, Size imgSize, OutputArray H1, OutputArray H2, double threshold=5)
	计算未经校准的立体摄像机的校正变换。
void	cv::triangulatePoints (InputArray projMatr1, InputArray projMatr2, InputArray projPoints1, InputArray projPoints2, OutputArray points4D)
	此函数通过使用立体摄像机的观测数据重建3D点（齐次坐标）。
void	cv::undistort (InputArray src, OutputArray dst, InputArray cameraMatrix, InputArray distCoeffs, InputArray newCameraMatrix=noArray())
	变换图像以补偿镜头畸变。
void	cv::undistortImagePoints (InputArray src, OutputArray dst, InputArray cameraMatrix, InputArray distCoeffs, TermCriteria=TermCriteria(TermCriteria::MAX_ITER+TermCriteria::EPS, 5, 0.01))
	计算畸变校正后的图像点位置。
void	cv::undistortPoints (InputArray src, OutputArray dst, InputArray cameraMatrix, InputArray distCoeffs, InputArray R, InputArray P, TermCriteria criteria)
void	cv::undistortPoints (InputArray src, OutputArray dst, InputArray cameraMatrix, InputArray distCoeffs, InputArray R=noArray(), InputArray P=noArray())
	从观测点坐标计算理想点坐标。
void	cv::validateDisparity (InputOutputArray disparity, InputArray cost, int minDisparity, int numberOfDisparities, int disp12MaxDisp=1)
	使用左右检查验证视差。“cost”矩阵应由立体对应算法计算得出。

类型定义文档

CirclesGridFinderParameters2

typedef CirclesGridFinderParameters cv::CirclesGridFinderParameters2

#include <opencv2/calib3d.hpp>

枚举类型文档

匿名枚举

匿名枚举

#include <opencv2/calib3d.hpp>

鲁棒估计算法类型

枚举器
LMEDS  Python: cv.LMEDS	最小中值平方算法
RANSAC  Python: cv.RANSAC	RANSAC算法。
RHO  Python: cv.RHO	RHO算法。
USAC_DEFAULT  Python: cv.USAC_DEFAULT	USAC算法，默认设置。
USAC_PARALLEL  Python: cv.USAC_PARALLEL	USAC，并行版本。
USAC_FM_8PTS  Python: cv.USAC_FM_8PTS	USAC，基本矩阵8点。
USAC_FAST  Python: cv.USAC_FAST	USAC，快速设置。
USAC_ACCURATE  Python: cv.USAC_ACCURATE	USAC，精确设置。
USAC_PROSAC  Python: cv.USAC_PROSAC	USAC，排序点，运行PROSAC。
USAC_MAGSAC  Python: cv.USAC_MAGSAC	USAC，运行MAGSAC++。

匿名枚举

匿名枚举

#include <opencv2/calib3d.hpp>

枚举器
CALIB_CB_ADAPTIVE_THRESH  Python: cv.CALIB_CB_ADAPTIVE_THRESH
CALIB_CB_NORMALIZE_IMAGE  Python: cv.CALIB_CB_NORMALIZE_IMAGE
CALIB_CB_FILTER_QUADS  Python: cv.CALIB_CB_FILTER_QUADS
CALIB_CB_FAST_CHECK  Python: cv.CALIB_CB_FAST_CHECK
CALIB_CB_EXHAUSTIVE  Python: cv.CALIB_CB_EXHAUSTIVE
CALIB_CB_ACCURACY  Python: cv.CALIB_CB_ACCURACY
CALIB_CB_LARGER  Python: cv.CALIB_CB_LARGER
CALIB_CB_MARKER  Python: cv.CALIB_CB_MARKER
CALIB_CB_PLAIN  Python: cv.CALIB_CB_PLAIN

匿名枚举

匿名枚举

#include <opencv2/calib3d.hpp>

枚举器
CALIB_CB_SYMMETRIC_GRID  Python: cv.CALIB_CB_SYMMETRIC_GRID
CALIB_CB_ASYMMETRIC_GRID  Python: cv.CALIB_CB_ASYMMETRIC_GRID
CALIB_CB_CLUSTERING  Python: cv.CALIB_CB_CLUSTERING

匿名枚举

匿名枚举

#include <opencv2/calib3d.hpp>

枚举器
CALIB_NINTRINSIC  Python: cv.CALIB_NINTRINSIC
CALIB_USE_INTRINSIC_GUESS  Python: cv.CALIB_USE_INTRINSIC_GUESS
CALIB_FIX_ASPECT_RATIO  Python: cv.CALIB_FIX_ASPECT_RATIO
CALIB_FIX_PRINCIPAL_POINT  Python: cv.CALIB_FIX_PRINCIPAL_POINT
CALIB_ZERO_TANGENT_DIST  Python: cv.CALIB_ZERO_TANGENT_DIST
CALIB_FIX_FOCAL_LENGTH  Python: cv.CALIB_FIX_FOCAL_LENGTH
CALIB_FIX_K1  Python: cv.CALIB_FIX_K1
CALIB_FIX_K2  Python: cv.CALIB_FIX_K2
CALIB_FIX_K3  Python: cv.CALIB_FIX_K3
CALIB_FIX_K4  Python: cv.CALIB_FIX_K4
CALIB_FIX_K5  Python: cv.CALIB_FIX_K5
CALIB_FIX_K6  Python: cv.CALIB_FIX_K6
CALIB_RATIONAL_MODEL  Python: cv.CALIB_RATIONAL_MODEL
CALIB_THIN_PRISM_MODEL  Python: cv.CALIB_THIN_PRISM_MODEL
CALIB_FIX_S1_S2_S3_S4  Python: cv.CALIB_FIX_S1_S2_S3_S4
CALIB_TILTED_MODEL  Python: cv.CALIB_TILTED_MODEL
CALIB_FIX_TAUX_TAUY  Python: cv.CALIB_FIX_TAUX_TAUY
CALIB_USE_QR  Python: cv.CALIB_USE_QR	使用QR而非SVD分解进行求解。更快但可能精度较低
CALIB_FIX_TANGENT_DIST  Python: cv.CALIB_FIX_TANGENT_DIST
CALIB_FIX_INTRINSIC  Python: cv.CALIB_FIX_INTRINSIC
CALIB_SAME_FOCAL_LENGTH  Python: cv.CALIB_SAME_FOCAL_LENGTH
CALIB_ZERO_DISPARITY  Python: cv.CALIB_ZERO_DISPARITY
CALIB_USE_LU  Python: cv.CALIB_USE_LU	使用LU而非SVD分解进行求解。快得多但可能精度较低
CALIB_USE_EXTRINSIC_GUESS  Python: cv.CALIB_USE_EXTRINSIC_GUESS	用于stereoCalibrate

匿名枚举

匿名枚举

#include <opencv2/calib3d.hpp>

查找基本矩阵的算法

枚举器
FM_7POINT  Python: cv.FM_7POINT	7点算法
FM_8POINT  Python: cv.FM_8POINT	8点算法
FM_LMEDS  Python: cv.FM_LMEDS	最小中值算法。使用7点算法。
FM_RANSAC  Python: cv.FM_RANSAC	RANSAC算法。需要至少15个点。使用7点算法。

HandEyeCalibrationMethod

枚举 cv::HandEyeCalibrationMethod

#include <opencv2/calib3d.hpp>

枚举器
CALIB_HAND_EYE_TSAI  Python: cv.CALIB_HAND_EYE_TSAI	《一种全自主高效3D机器人手眼校准新技术》[277]。
CALIB_HAND_EYE_PARK  Python: cv.CALIB_HAND_EYE_PARK	《机器人传感器校准：在欧几里得群上求解 AX = XB》[216]。
CALIB_HAND_EYE_HORAUD  Python: cv.CALIB_HAND_EYE_HORAUD	《手眼校准》[129]。
CALIB_HAND_EYE_ANDREFF  Python: cv.CALIB_HAND_EYE_ANDREFF	《在线手眼校准》[13]。
CALIB_HAND_EYE_DANIILIDIS  Python: cv.CALIB_HAND_EYE_DANIILIDIS	《使用对偶四元数进行手眼校准》[67]。

LocalOptimMethod

枚举 cv::LocalOptimMethod

#include <opencv2/calib3d.hpp>

枚举器
LOCAL_OPTIM_NULL  Python: cv.LOCAL_OPTIM_NULL
LOCAL_OPTIM_INNER_LO  Python: cv.LOCAL_OPTIM_INNER_LO
LOCAL_OPTIM_INNER_AND_ITER_LO  Python: cv.LOCAL_OPTIM_INNER_AND_ITER_LO
LOCAL_OPTIM_GC  Python: cv.LOCAL_OPTIM_GC
LOCAL_OPTIM_SIGMA  Python: cv.LOCAL_OPTIM_SIGMA

NeighborSearchMethod

枚举 cv::NeighborSearchMethod

#include <opencv2/calib3d.hpp>

枚举器
NEIGH_FLANN_KNN  Python: cv.NEIGH_FLANN_KNN
NEIGH_GRID  Python: cv.NEIGH_GRID
NEIGH_FLANN_RADIUS  Python: cv.NEIGH_FLANN_RADIUS

PolishingMethod

枚举 cv::PolishingMethod

#include <opencv2/calib3d.hpp>

枚举器
NONE_POLISHER  Python: cv.NONE_POLISHER
LSQ_POLISHER  Python: cv.LSQ_POLISHER
MAGSAC  Python: cv.MAGSAC
COV_POLISHER  Python: cv.COV_POLISHER

RobotWorldHandEyeCalibrationMethod

枚举 cv::RobotWorldHandEyeCalibrationMethod

#include <opencv2/calib3d.hpp>

枚举器
CALIB_ROBOT_WORLD_HAND_EYE_SHAH  Python: cv.CALIB_ROBOT_WORLD_HAND_EYE_SHAH	《使用克罗内克积求解机器人-世界/手眼校准问题》[247]。
CALIB_ROBOT_WORLD_HAND_EYE_LI  Python: cv.CALIB_ROBOT_WORLD_HAND_EYE_LI	《使用对偶四元数和克罗内克积同时进行机器人-世界和手眼校准》[165]。

SamplingMethod

枚举 cv::SamplingMethod

#include <opencv2/calib3d.hpp>

枚举器
SAMPLING_UNIFORM  Python: cv.SAMPLING_UNIFORM
SAMPLING_PROGRESSIVE_NAPSAC  Python: cv.SAMPLING_PROGRESSIVE_NAPSAC
SAMPLING_NAPSAC  Python: cv.SAMPLING_NAPSAC
SAMPLING_PROSAC  Python: cv.SAMPLING_PROSAC

ScoreMethod

枚举 cv::ScoreMethod

#include <opencv2/calib3d.hpp>

枚举器
SCORE_METHOD_RANSAC  Python: cv.SCORE_METHOD_RANSAC
SCORE_METHOD_MSAC  Python: cv.SCORE_METHOD_MSAC
SCORE_METHOD_MAGSAC  Python: cv.SCORE_METHOD_MAGSAC
SCORE_METHOD_LMEDS  Python: cv.SCORE_METHOD_LMEDS

SolvePnPMethod

枚举 cv::SolvePnPMethod

#include <opencv2/calib3d.hpp>

枚举器
SOLVEPNP_ITERATIVE  Python: cv.SOLVEPNP_ITERATIVE	使用非线性Levenberg-Marquardt最小化方案进行姿态优化[181] [79] 非平面“objectPoints”的初始解至少需要6个点，并使用DLT算法。 平面“objectPoints”的初始解至少需要4个点，并使用从单应分解得到的姿态。
SOLVEPNP_EPNP  Python: cv.SOLVEPNP_EPNP	EPnP：高效透视-n点相机姿态估计[160]。
SOLVEPNP_P3P  Python: cv.SOLVEPNP_P3P	《透视三点问题的完整解分类》[99]。
SOLVEPNP_DLS  Python: cv.SOLVEPNP_DLS	损坏的实现。使用此标志将回退到EPnP。 PnP的直接最小二乘(DLS)方法[127]
SOLVEPNP_UPNP  Python: cv.SOLVEPNP_UPNP	损坏的实现。使用此标志将回退到EPnP。 《用于鲁棒相机姿态和焦距估计的穷举线性化》[217]
SOLVEPNP_AP3P  Python: cv.SOLVEPNP_AP3P	《透视三点问题的高效代数解》[147]。
SOLVEPNP_IPPE  Python: cv.SOLVEPNP_IPPE	《基于无穷小平面的姿态估计》[63] 物体点必须共面。
SOLVEPNP_IPPE_SQUARE  Python: cv.SOLVEPNP_IPPE_SQUARE	《基于无穷小平面的姿态估计》[63] 这是适用于标记姿态估计的特殊情况。 4个共面物体点必须按以下顺序定义 点 0: [-squareLength / 2, squareLength / 2, 0] 点 1: [ squareLength / 2, squareLength / 2, 0] 点 2: [ squareLength / 2, -squareLength / 2, 0] 点 3: [-squareLength / 2, -squareLength / 2, 0]
SOLVEPNP_SQPNP  Python: cv.SOLVEPNP_SQPNP	SQPnP：透视-n点问题的一致快速且全局最优解[271]。

UndistortTypes

枚举 cv::UndistortTypes

#include <opencv2/calib3d.hpp>

cv::undistort 模式

枚举器
PROJ_SPHERICAL_ORTHO  Python: cv.PROJ_SPHERICAL_ORTHO
PROJ_SPHERICAL_EQRECT  Python: cv.PROJ_SPHERICAL_EQRECT

函数文档

calibrateCamera() [1/2]

double cv::calibrateCamera	(	InputArrayOfArrays	objectPoints,
		InputArrayOfArrays	imagePoints,
		Size	imageSize,
		InputOutputArray	cameraMatrix,
		InputOutputArray	distCoeffs,
		OutputArrayOfArrays	rvecs,
		OutputArrayOfArrays	tvecs,
		int	flags = 0,
		TermCriteria	criteria = TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 30, DBL_EPSILON) )

Python
	cv.calibrateCamera(	objectPoints, imagePoints, imageSize, cameraMatrix, distCoeffs[, rvecs[, tvecs[, flags[, criteria]]]]	) ->	retval, cameraMatrix, distCoeffs, rvecs, tvecs
	cv.calibrateCameraExtended(	objectPoints, imagePoints, imageSize, cameraMatrix, distCoeffs[, rvecs[, tvecs[, stdDeviationsIntrinsics[, stdDeviationsExtrinsics[, perViewErrors[, flags[, criteria]]]]]]]	) ->	retval, cameraMatrix, distCoeffs, rvecs, tvecs, stdDeviationsIntrinsics, stdDeviationsExtrinsics, perViewErrors

#include <opencv2/calib3d.hpp>

这是一个重载的成员函数，为方便起见而提供。它与上述函数的区别仅在于它接受的参数。

calibrateCamera() [2/2]

double cv::calibrateCamera	(	InputArrayOfArrays	objectPoints,
		InputArrayOfArrays	imagePoints,
		Size	imageSize,
		InputOutputArray	cameraMatrix,
		InputOutputArray	distCoeffs,
		OutputArrayOfArrays	rvecs,
		OutputArrayOfArrays	tvecs,
		OutputArray	stdDeviationsIntrinsics,
		OutputArray	stdDeviationsExtrinsics,
		OutputArray	perViewErrors,
		int	flags = 0,
		TermCriteria	criteria = TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 30, DBL_EPSILON) )

Python
	cv.calibrateCamera(	objectPoints, imagePoints, imageSize, cameraMatrix, distCoeffs[, rvecs[, tvecs[, flags[, criteria]]]]	) ->	retval, cameraMatrix, distCoeffs, rvecs, tvecs
	cv.calibrateCameraExtended(	objectPoints, imagePoints, imageSize, cameraMatrix, distCoeffs[, rvecs[, tvecs[, stdDeviationsIntrinsics[, stdDeviationsExtrinsics[, perViewErrors[, flags[, criteria]]]]]]]	) ->	retval, cameraMatrix, distCoeffs, rvecs, tvecs, stdDeviationsIntrinsics, stdDeviationsExtrinsics, perViewErrors

#include <opencv2/calib3d.hpp>

从标定模式的多个视图中查找相机内参和外参。

参数

objectPoints	在新接口中，它是校准模式点在校准模式坐标空间中的向量的向量（例如 std::vector<std::vector<cv::Vec3f>>）。外部向量包含与模式视图数量相同的元素。如果每个视图中显示相同的校准模式且完全可见，则所有向量将相同。但是，也可以在不同视图中使用部分遮挡的模式甚至不同的模式。然后，向量将不同。虽然这些点是3D的，但如果使用的校准模式是平面装置，它们都位于校准模式的XY坐标平面中（因此Z坐标为0）。在旧接口中，所有来自不同视图的物体点向量都连接在一起。
imagePoints	在新接口中，它是校准模式点投影的向量的向量（例如 std::vector<std::vector<cv::Vec2f>>）。imagePoints.size() 和 objectPoints.size()，以及每个 i 的 imagePoints[i].size() 和 objectPoints[i].size() 必须分别相等。在旧接口中，所有来自不同视图的物体点向量都连接在一起。
imageSize	仅用于初始化相机内参矩阵的图像大小。
cameraMatrix	输入/输出3x3浮点相机内参矩阵 \(\cameramatrix{A}\)。如果指定了 CALIB_USE_INTRINSIC_GUESS 和/或 CALIB_FIX_ASPECT_RATIO、CALIB_FIX_PRINCIPAL_POINT 或 CALIB_FIX_FOCAL_LENGTH，则必须在调用函数之前初始化部分或全部 fx、fy、cx、cy。
distCoeffs	畸变系数向量 \(\distcoeffs\) 的输入/输出。
rvecs	为每个模式视图估计的旋转向量输出向量（Rodrigues）（例如 std::vector<cv::Mat>>）。也就是说，每个第i个旋转向量以及相应的第i个平移向量（见下一个输出参数描述）将校准模式从物体坐标空间（其中指定了物体点）带到相机坐标空间。更技术性地说，第i个旋转向量和平移向量的元组执行从物体坐标空间到相机坐标空间的基础变换。由于其对偶性，此元组等同于校准模式相对于相机坐标空间的位置。
tvecs	为每个模式视图估计的平移向量输出向量，详见上述参数描述。
stdDeviationsIntrinsics	为内参估计的标准偏差输出向量。偏差值顺序：\((f_x, f_y, c_x, c_y, k_1, k_2, p_1, p_2, k_3, k_4, k_5, k_6 , s_1, s_2, s_3, s_4, \tau_x, \tau_y)\)。如果其中一个参数未被估计，则其偏差等于零。
stdDeviationsExtrinsics	外参估计的标准偏差输出向量。偏差值顺序：\((R_0, T_0, \dotsc , R_{M - 1}, T_{M - 1})\)，其中M是模式视图的数量。\ (R_i, T_i\) 是连接的1x3向量。
perViewErrors	为每个模式视图估计的RMS重投影误差输出向量。
flags	可以为零或以下值的组合的不同标志 CALIB_USE_INTRINSIC_GUESS cameraMatrix 包含 fx, fy, cx, cy 的有效初始值，这些值会进一步优化。否则，(cx, cy) 初始设置为图像中心（使用 imageSize），焦距以最小二乘方式计算。请注意，如果内参已知，则无需使用此函数来估计外参。请改用 solvePnP。 CALIB_FIX_PRINCIPAL_POINT 主点在全局优化期间不发生变化。它保持在中心或当 CALIB_USE_INTRINSIC_GUESS 也设置时指定的其他位置。 CALIB_FIX_ASPECT_RATIO 函数只将 fy 视为自由参数。fx/fy 的比率与输入 cameraMatrix 中的比率保持相同。当 CALIB_USE_INTRINSIC_GUESS 未设置时，fx 和 fy 的实际输入值将被忽略，只计算并使用它们的比率。 CALIB_ZERO_TANGENT_DIST 切向畸变系数 \((p_1, p_2)\) 设置为零并保持为零。 CALIB_FIX_FOCAL_LENGTH 如果设置了 CALIB_USE_INTRINSIC_GUESS，则焦距在全局优化期间不发生变化。 CALIB_FIX_K1,..., CALIB_FIX_K6 对应的径向畸变系数在优化期间不发生变化。如果设置了 CALIB_USE_INTRINSIC_GUESS，则使用提供的 distCoeffs 矩阵中的系数。否则，将其设置为0。 CALIB_RATIONAL_MODEL 启用系数 k4、k5 和 k6。为了提供向后兼容性，应明确指定此额外标志，使校准函数使用有理模型并返回8个或更多系数。 CALIB_THIN_PRISM_MODEL 启用系数 s1、s2、s3 和 s4。为了提供向后兼容性，应明确指定此额外标志，使校准函数使用薄棱镜模型并返回12个或更多系数。 CALIB_FIX_S1_S2_S3_S4 薄棱镜畸变系数在优化期间不发生变化。如果设置了 CALIB_USE_INTRINSIC_GUESS，则使用提供的 distCoeffs 矩阵中的系数。否则，将其设置为0。 CALIB_TILTED_MODEL 启用系数 tauX 和 tauY。为了提供向后兼容性，应明确指定此额外标志，使校准函数使用倾斜传感器模型并返回14个系数。 CALIB_FIX_TAUX_TAUY 倾斜传感器模型的系数在优化期间不发生变化。如果设置了 CALIB_USE_INTRINSIC_GUESS，则使用提供的 distCoeffs 矩阵中的系数。否则，将其设置为0。
criteria	迭代优化算法的终止条件。

返回

整体 RMS 重投影误差。

该函数估计每个视图的相机内参和外参。该算法基于[321]和[38]。必须指定3D物体点的坐标及其在每个视图中的对应2D投影。这可以通过使用已知几何形状和易于检测的特征点的物体来实现。这样的物体称为校准装置或校准模式，OpenCV内置支持棋盘作为校准装置（参见findChessboardCorners）。目前，内参的初始化（当未设置CALIB_USE_INTRINSIC_GUESS时）仅针对平面校准模式（其中物体点的Z坐标必须全部为零）实现。只要提供了初始cameraMatrix，也可以使用3D校准装置。

该算法执行以下步骤

• 计算初始内参（此选项仅适用于平面校准模式）或从输入参数中读取它们。畸变系数初始全部设置为零，除非指定了某些 CALIB_FIX_K?。
• 估计初始相机姿态，如同内参已已知。这通过使用 solvePnP 完成。
• 运行全局Levenberg-Marquardt优化算法，以最小化重投影误差，即观察到的特征点imagePoints与投影（使用当前相机参数和姿态估计）物体点objectPoints之间的平方距离总和。有关详细信息，请参阅projectPoints。

注意

如果您使用非正方形（即非 N×N）网格并使用 findChessboardCorners 进行校准，并且 calibrateCamera 返回错误值（零畸变系数， \(c_x\) 和 \(c_y\) 距离图像中心很远，和/或 \(f_x\) 和 \(f_y\) 之间差异很大（比例为10:1或更高）），那么您可能在 findChessboardCorners 中使用了 patternSize=cvSize(rows,cols) 而不是 patternSize=cvSize(cols,rows)。

如果提供了不受支持的参数组合或系统欠约束，该函数可能会抛出异常。

另请参见

calibrateCameraRO, findChessboardCorners, solvePnP, initCameraMatrix2D, stereoCalibrate, undistort

calibrateCameraRO() [1/2]

double cv::calibrateCameraRO	(	InputArrayOfArrays	objectPoints,
		InputArrayOfArrays	imagePoints,
		Size	imageSize,
		int	iFixedPoint,
		InputOutputArray	cameraMatrix,
		InputOutputArray	distCoeffs,
		OutputArrayOfArrays	rvecs,
		OutputArrayOfArrays	tvecs,
		OutputArray	newObjPoints,
		int	flags = 0,
		TermCriteria	criteria = TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 30, DBL_EPSILON) )

Python
	cv.calibrateCameraRO(	objectPoints, imagePoints, imageSize, iFixedPoint, cameraMatrix, distCoeffs[, rvecs[, tvecs[, newObjPoints[, flags[, criteria]]]]]	) ->	retval, cameraMatrix, distCoeffs, rvecs, tvecs, newObjPoints
	cv.calibrateCameraROExtended(	objectPoints, imagePoints, imageSize, iFixedPoint, cameraMatrix, distCoeffs[, rvecs[, tvecs[, newObjPoints[, stdDeviationsIntrinsics[, stdDeviationsExtrinsics[, stdDeviationsObjPoints[, perViewErrors[, flags[, criteria]]]]]]]]]	) ->	retval, cameraMatrix, distCoeffs, rvecs, tvecs, newObjPoints, stdDeviationsIntrinsics, stdDeviationsExtrinsics, stdDeviationsObjPoints, perViewErrors

#include <opencv2/calib3d.hpp>

这是一个重载的成员函数，为方便起见而提供。它与上述函数的区别仅在于它接受的参数。

calibrateCameraRO() [2/2]

double cv::calibrateCameraRO	(	InputArrayOfArrays	objectPoints,
		InputArrayOfArrays	imagePoints,
		Size	imageSize,
		int	iFixedPoint,
		InputOutputArray	cameraMatrix,
		InputOutputArray	distCoeffs,
		OutputArrayOfArrays	rvecs,
		OutputArrayOfArrays	tvecs,
		OutputArray	newObjPoints,
		OutputArray	stdDeviationsIntrinsics,
		OutputArray	stdDeviationsExtrinsics,
		OutputArray	stdDeviationsObjPoints,
		OutputArray	perViewErrors,
		int	flags = 0,
		TermCriteria	criteria = TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 30, DBL_EPSILON) )

Python
	cv.calibrateCameraRO(	objectPoints, imagePoints, imageSize, iFixedPoint, cameraMatrix, distCoeffs[, rvecs[, tvecs[, newObjPoints[, flags[, criteria]]]]]	) ->	retval, cameraMatrix, distCoeffs, rvecs, tvecs, newObjPoints
	cv.calibrateCameraROExtended(	objectPoints, imagePoints, imageSize, iFixedPoint, cameraMatrix, distCoeffs[, rvecs[, tvecs[, newObjPoints[, stdDeviationsIntrinsics[, stdDeviationsExtrinsics[, stdDeviationsObjPoints[, perViewErrors[, flags[, criteria]]]]]]]]]	) ->	retval, cameraMatrix, distCoeffs, rvecs, tvecs, newObjPoints, stdDeviationsIntrinsics, stdDeviationsExtrinsics, stdDeviationsObjPoints, perViewErrors

#include <opencv2/calib3d.hpp>

从标定模式的多个视图中查找相机内参和外参。

此函数是 calibrateCamera 的扩展，采用了 [258] 中提出的释放物体方法。在许多常见情况下，对于不精确、未测量、大致平面的目标（校准板），此方法可以显著提高估计相机参数的精度。此函数支持释放物体方法和标准方法。使用参数 iFixedPoint 进行方法选择。在内部实现中，calibrateCamera 是此函数的一个封装器。

参数

objectPoints	校准模式点在校准模式坐标空间中的向量的向量。详见calibrateCamera。如果使用释放物体方法，则每个视图中必须使用相同的校准板且必须完全可见，并且所有 objectPoints[i] 必须相同，所有点应大致接近一个平面。校准目标必须是刚性的，或者至少在移动相机（而不是校准目标）以捕捉图像时是静态的。
imagePoints	校准模式点投影的向量的向量。详见calibrateCamera。
imageSize	仅用于初始化相机内参矩阵的图像大小。
iFixedPoint	要固定的 objectPoints[0] 中3D物体点的索引。它也作为校准方法选择的开关。如果使用释放物体方法，则传入参数的范围应在 [1, objectPoints[0].size()-2] 内，否则超出此范围的值将选择标准校准方法。通常建议在使用释放物体方法时，将校准板网格的右上角点固定。根据[258]，另外两个点也被固定。在此实现中，使用了 objectPoints[0].front 和 objectPoints[0].back.z。使用释放物体方法，只有当这三个固定点的坐标足够精确时，才能获得精确的rvecs、tvecs和newObjPoints。
cameraMatrix	输出3x3浮点相机矩阵。详见calibrateCamera。
distCoeffs	畸变系数输出向量。详见calibrateCamera。
rvecs	为每个模式视图估计的旋转向量输出向量。详见calibrateCamera。
tvecs	为每个模式视图估计的平移向量输出向量。
newObjPoints	校准模式点的更新输出向量。坐标可能会根据三个固定点进行缩放。返回的坐标只有在上述三个固定点精确时才精确。如果不需要，可以传入noArray()。标准校准方法会忽略此参数。
stdDeviationsIntrinsics	为内参估计的标准偏差输出向量。详见calibrateCamera。
stdDeviationsExtrinsics	外参估计的标准偏差输出向量。详见calibrateCamera。
stdDeviationsObjPoints	校准模式点精细坐标的标准偏差输出向量。它与 objectPoints[0] 向量具有相同的大小和顺序。标准校准方法会忽略此参数。
perViewErrors	为每个模式视图估计的RMS重投影误差输出向量。
flags	可以为零或一些预定义值的组合的不同标志。详见calibrateCamera。如果使用释放物体方法，校准时间可能会更长。CALIB_USE_QR 或 CALIB_USE_LU 可用于更快但某些情况下可能精度较低且不稳定的校准。
criteria	迭代优化算法的终止条件。

返回

整体 RMS 重投影误差。

该函数估计每个视图的相机内参和外参。该算法基于[321]、[38]和[258]。有关其他详细说明，请参阅calibrateCamera。

另请参见

calibrateCamera, findChessboardCorners, solvePnP, initCameraMatrix2D, stereoCalibrate, undistort

calibrateHandEye()

void cv::calibrateHandEye	(	InputArrayOfArrays	R_gripper2base,
		InputArrayOfArrays	t_gripper2base,
		InputArrayOfArrays	R_target2cam,
		InputArrayOfArrays	t_target2cam,
		OutputArray	R_cam2gripper,
		OutputArray	t_cam2gripper,
		HandEyeCalibrationMethod	method = CALIB_HAND_EYE_TSAI )

Python
	cv.calibrateHandEye(	R_gripper2base, t_gripper2base, R_target2cam, t_target2cam[, R_cam2gripper[, t_cam2gripper[, method]]]	) ->	R_cam2gripper, t_cam2gripper

#include <opencv2/calib3d.hpp>

计算手眼标定：\(_{}^{g}\textrm{T}_c\)。

参数

[输入]	R_gripper2base	从将夹持器坐标系中的点转换到机器人基坐标系（\(_{}^{b}\textrm{T}_g\)）的齐次矩阵中提取的旋转部分。这是一个向量（vector<Mat>），其中包含从夹持器坐标系到机器人基坐标系所有变换的旋转矩阵（3x3）或旋转向量（3x1）。
[输入]	t_gripper2base	从将夹持器坐标系中的点转换到机器人基坐标系（\(_{}^{b}\textrm{T}_g\)）的齐次矩阵中提取的平移部分。这是一个向量（vector<Mat>），其中包含从夹持器坐标系到机器人基坐标系所有变换的3x1平移向量。
[输入]	R_target2cam	从将目标坐标系中的点转换到相机坐标系（\(_{}^{c}\textrm{T}_t\)）的齐次矩阵中提取的旋转部分。这是一个向量（vector<Mat>），其中包含从校准目标坐标系到相机坐标系所有变换的旋转矩阵（3x3）或旋转向量（3x1）。
[输入]	t_target2cam	从将目标坐标系中的点转换到相机坐标系（\(_{}^{c}\textrm{T}_t\)）的齐次矩阵中提取的旋转部分。这是一个向量（vector<Mat>），其中包含从校准目标坐标系到相机坐标系所有变换的3x1平移向量。
[输出]	R_cam2gripper	从将相机坐标系中的点转换到夹持器坐标系（\(_{}^{g}\textrm{T}_c\)）的齐次矩阵中提取的估计3x3旋转部分。
[输出]	t_cam2gripper	从将相机坐标系中的点转换到夹持器坐标系（\(_{}^{g}\textrm{T}_c\)）的齐次矩阵中提取的估计3x1平移部分。
[输入]	方法	已实现的手眼校准方法之一，请参阅cv::HandEyeCalibrationMethod

该函数使用各种方法进行手眼校准。一种方法是先估计旋转，然后估计平移（可分离解），并实现了以下方法

• R. Tsai, R. Lenz 《一种全自主高效3D机器人手眼校准新技术》[277]
• F. Park, B. Martin 《机器人传感器校准：在欧几里得群上求解 AX = XB》[216]
• R. Horaud, F. Dornaika 《手眼校准》[129]

另一种方法是同时估计旋转和平移（同步解），并实现了以下方法

• N. Andreff, R. Horaud, B. Espiau 《在线手眼校准》[13]
• K. Daniilidis 《使用对偶四元数进行手眼校准》[67]

下图描述了手眼校准问题，其中需要估计安装在机器人夹持器（“手”）上的相机（“眼”）之间的变换。这种配置称为眼在手。

手在外配置是指静态相机观察安装在机器人末端执行器上的校准模式。然后可以通过向函数输入合适的变换来估计从相机到机器人基座标系的变换，如下所示。

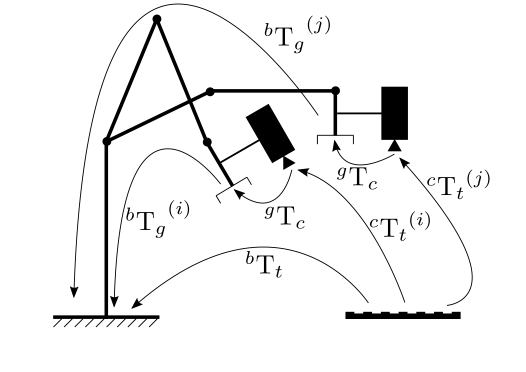
校准过程如下

• 使用静态校准模式来估计目标坐标系和相机坐标系之间的变换
• 移动机器人夹持器以获取多个姿态
• 对于每个姿态，记录夹持器坐标系和机器人基坐标系之间的齐次变换，例如使用机器人运动学

  \[ \begin{bmatrix} X_b\\ Y_b\\ Z_b\\ 1 \end{bmatrix} = \begin{bmatrix} _{}^{b}\textrm{R}_g & _{}^{b}\textrm{t}_g \\ 0_{1 \times 3} & 1 \end{bmatrix} \begin{bmatrix} X_g\\ Y_g\\ Z_g\\ 1 \end{bmatrix} \]

• 对于每个姿态，记录校准目标坐标系和相机坐标系之间的齐次变换，例如使用2D-3D点对应关系的姿态估计方法（PnP）

  \[ \begin{bmatrix} X_c\\ Y_c\\ Z_c\\ 1 \end{bmatrix} = \begin{bmatrix} _{}^{c}\textrm{R}_t & _{}^{c}\textrm{t}_t \\ 0_{1 \times 3} & 1 \end{bmatrix} \begin{bmatrix} X_t\\ Y_t\\ Z_t\\ 1 \end{bmatrix} \]

手眼校准过程返回以下齐次变换

\[ \begin{bmatrix} X_g\\ Y_g\\ Z_g\\ 1 \end{bmatrix} = \begin{bmatrix} _{}^{g}\textrm{R}_c & _{}^{g}\textrm{t}_c \\ 0_{1 \times 3} & 1 \end{bmatrix} \begin{bmatrix} X_c\\ Y_c\\ Z_c\\ 1 \end{bmatrix} \]

这个问题也称为求解 \(\mathbf{A}\mathbf{X}=\mathbf{X}\mathbf{B}\) 方程

• 对于眼在手配置

  \[ \begin{align*} ^{b}{\textrm{T}_g}^{(1)} \hspace{0.2em} ^{g}\textrm{T}_c \hspace{0.2em} ^{c}{\textrm{T}_t}^{(1)} &= \hspace{0.1em} ^{b}{\textrm{T}_g}^{(2)} \hspace{0.2em} ^{g}\textrm{T}_c \hspace{0.2em} ^{c}{\textrm{T}_t}^{(2)} \\ (^{b}{\textrm{T}_g}^{(2)})^{-1} \hspace{0.2em} ^{b}{\textrm{T}_g}^{(1)} \hspace{0.2em} ^{g}\textrm{T}_c &= \hspace{0.1em} ^{g}\textrm{T}_c \hspace{0.2em} ^{c}{\textrm{T}_t}^{(2)} (^{c}{\textrm{T}_t}^{(1)})^{-1} \\ \textrm{A}_i \textrm{X} &= \textrm{X} \textrm{B}_i \\ \end{align*} \]

• 对于手在外配置

  \[ \begin{align*} ^{g}{\textrm{T}_b}^{(1)} \hspace{0.2em} ^{b}\textrm{T}_c \hspace{0.2em} ^{c}{\textrm{T}_t}^{(1)} &= \hspace{0.1em} ^{g}{\textrm{T}_b}^{(2)} \hspace{0.2em} ^{b}\textrm{T}_c \hspace{0.2em} ^{c}{\textrm{T}_t}^{(2)} \\ (^{g}{\textrm{T}_b}^{(2)})^{-1} \hspace{0.2em} ^{g}{\textrm{T}_b}^{(1)} \hspace{0.2em} ^{b}\textrm{T}_c &= \hspace{0.1em} ^{b}\textrm{T}_c \hspace{0.2em} ^{c}{\textrm{T}_t}^{(2)} (^{c}{\textrm{T}_t}^{(1)})^{-1} \\ \textrm{A}_i \textrm{X} &= \textrm{X} \textrm{B}_i \\ \end{align*} \]

注意

更多信息可访问此网站。

至少需要2个非平行旋转轴的运动才能确定手眼变换。因此至少需要3个不同的姿态，但强烈建议使用更多的姿态。

calibrateRobotWorldHandEye()

void cv::calibrateRobotWorldHandEye	(	InputArrayOfArrays	R_world2cam,
		InputArrayOfArrays	t_world2cam,
		InputArrayOfArrays	R_base2gripper,
		InputArrayOfArrays	t_base2gripper,
		OutputArray	R_base2world,
		OutputArray	t_base2world,
		OutputArray	R_gripper2cam,
		OutputArray	t_gripper2cam,
		RobotWorldHandEyeCalibrationMethod	method = CALIB_ROBOT_WORLD_HAND_EYE_SHAH )

Python
	cv.calibrateRobotWorldHandEye(	R_world2cam, t_world2cam, R_base2gripper, t_base2gripper[, R_base2world[, t_base2world[, R_gripper2cam[, t_gripper2cam[, method]]]]]	) ->	R_base2world, t_base2world, R_gripper2cam, t_gripper2cam

#include <opencv2/calib3d.hpp>

计算机器人-世界/手眼标定：\(_{}^{w}\textrm{T}_b\) 和 \(_{}^{c}\textrm{T}_g\)。

参数

[输入]	R_world2cam	从将世界坐标系中的点转换到相机坐标系（ \(_{}^{c}\textrm{T}_w\)）的齐次矩阵中提取的旋转部分。这是一个向量（vector<Mat>），包含所有从世界坐标系到相机坐标系的变换的旋转部分，即(3x3)旋转矩阵或(3x1)旋转向量。
[输入]	t_world2cam	从将世界坐标系中的点转换到相机坐标系（ \(_{}^{c}\textrm{T}_w\)）的齐次矩阵中提取的平移部分。这是一个向量（vector<Mat>），包含所有从世界坐标系到相机坐标系的变换的(3x1)平移向量。
[输入]	R_base2gripper	从将机器人基座坐标系中的点转换到夹具坐标系（ \(_{}^{g}\textrm{T}_b\)）的齐次矩阵中提取的旋转部分。这是一个向量（vector<Mat>），包含所有从机器人基座坐标系到夹具坐标系的变换的旋转部分，即(3x3)旋转矩阵或(3x1)旋转向量。
[输入]	t_base2gripper	从将机器人基座坐标系中的点转换到夹具坐标系（ \(_{}^{g}\textrm{T}_b\)）的齐次矩阵中提取的旋转部分。这是一个向量（vector<Mat>），包含所有从机器人基座坐标系到夹具坐标系的变换的(3x1)平移向量。
[输出]	R_base2world	从将机器人基座坐标系中的点转换到世界坐标系（ \(_{}^{w}\textrm{T}_b\)）的齐次矩阵中提取的估计(3x3)旋转部分。
[输出]	t_base2world	从将机器人基座坐标系中的点转换到世界坐标系（ \(_{}^{w}\textrm{T}_b\)）的齐次矩阵中提取的估计(3x1)平移部分。
[输出]	R_gripper2cam	从将夹具坐标系中的点转换到相机坐标系（ \(_{}^{c}\textrm{T}_g\)）的齐次矩阵中提取的估计(3x3)旋转部分。
[输出]	t_gripper2cam	从将夹具坐标系中的点转换到相机坐标系（ \(_{}^{c}\textrm{T}_g\)）的齐次矩阵中提取的估计(3x1)平移部分。
[输入]	方法	已实现的机器人-世界/手眼标定方法之一，参见cv::RobotWorldHandEyeCalibrationMethod

该函数使用多种方法执行机器人-世界/手眼标定。一种方法是先估计旋转，然后估计平移（可分离解）

• M. Shah, 使用克罗内克积解决机器人-世界/手眼标定问题 [247]

另一种方法是同时估计旋转和平移（同步解），通过以下已实现的方法

• A. Li, L. Wang, and D. Wu, 使用双四元数和克罗内克积同时进行机器人-世界和手眼标定 [165]

下图描述了机器人-世界/手眼标定问题，其中需要估计机器人与世界坐标系之间以及安装在机器人末端执行器上的机器人夹具（“手”）与相机（“眼”）之间的变换。

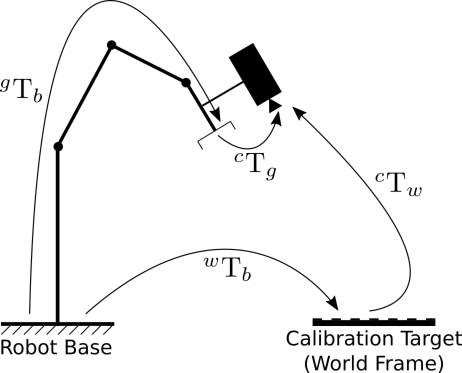
校准过程如下

• 使用静态校准模式来估计目标坐标系和相机坐标系之间的变换
• 移动机器人夹持器以获取多个姿态
• 对于每个姿态，记录夹持器坐标系和机器人基坐标系之间的齐次变换，例如使用机器人运动学

  \[ \begin{bmatrix} X_g\\ Y_g\\ Z_g\\ 1 \end{bmatrix} = \begin{bmatrix} _{}^{g}\textrm{R}_b & _{}^{g}\textrm{t}_b \\ 0_{1 \times 3} & 1 \end{bmatrix} \begin{bmatrix} X_b\\ Y_b\\ Z_b\\ 1 \end{bmatrix} \]

• 对于每个姿态，校准目标坐标系（世界坐标系）与相机坐标系之间的齐次变换会通过例如使用2D-3D点对应关系的姿态估计方法（PnP）进行记录

  \[ \begin{bmatrix} X_c\\ Y_c\\ Z_c\\ 1 \end{bmatrix} = \begin{bmatrix} _{}^{c}\textrm{R}_w & _{}^{c}\textrm{t}_w \\ 0_{1 \times 3} & 1 \end{bmatrix} \begin{bmatrix} X_w\\ Y_w\\ Z_w\\ 1 \end{bmatrix} \]

机器人-世界/手眼标定程序返回以下齐次变换

\[ \begin{bmatrix} X_w\\ Y_w\\ Z_w\\ 1 \end{bmatrix} = \begin{bmatrix} _{}^{w}\textrm{R}_b & _{}^{w}\textrm{t}_b \\ 0_{1 \times 3} & 1 \end{bmatrix} \begin{bmatrix} X_b\\ Y_b\\ Z_b\\ 1 \end{bmatrix} \]

\[ \begin{bmatrix} X_c\\ Y_c\\ Z_c\\ 1 \end{bmatrix} = \begin{bmatrix} _{}^{c}\textrm{R}_g & _{}^{c}\textrm{t}_g \\ 0_{1 \times 3} & 1 \end{bmatrix} \begin{bmatrix} X_g\\ Y_g\\ Z_g\\ 1 \end{bmatrix} \]

该问题也称为求解\(\mathbf{A}\mathbf{X}=\mathbf{Z}\mathbf{B}\)方程，其中：

• \(\mathbf{A} \Leftrightarrow \hspace{0.1em} _{}^{c}\textrm{T}_w\)
• \(\mathbf{X} \Leftrightarrow \hspace{0.1em} _{}^{w}\textrm{T}_b\)
• \(\mathbf{Z} \Leftrightarrow \hspace{0.1em} _{}^{c}\textrm{T}_g\)
• \(\mathbf{B} \Leftrightarrow \hspace{0.1em} _{}^{g}\textrm{T}_b\)

注意

至少需要3次测量（输入向量的大小必须大于或等于3）。

calibrationMatrixValues()

void cv::calibrationMatrixValues	(	InputArray	cameraMatrix,
		Size	imageSize,
		double	apertureWidth,
		double	apertureHeight,
		double &	fovx,
		double &	fovy,
		double &	focalLength,
		Point2d &	principalPoint,
		double &	aspectRatio )

Python
	cv.calibrationMatrixValues(	cameraMatrix, imageSize, apertureWidth, apertureHeight	) ->	fovx, fovy, focalLength, principalPoint, aspectRatio

#include <opencv2/calib3d.hpp>

根据相机内参矩阵计算有用的相机特性。

参数

cameraMatrix	输入相机内参矩阵，可通过calibrateCamera或stereoCalibrate进行估计。
imageSize	输入图像尺寸（像素）。
apertureWidth	传感器物理宽度（毫米）。
apertureHeight	传感器物理高度（毫米）。
fovx	输出沿水平传感器轴的视场角度（度）。
fovy	输出沿垂直传感器轴的视场角度（度）。
focalLength	镜头焦距（毫米）。
principalPoint	主点（毫米）。
aspectRatio	\(f_y/f_x\)

该函数从先前估计的相机矩阵计算各种有用的相机特性。

注意

请记住，单位“毫米”代表棋盘格间距所选择的任何测量单位（因此可以是任何值）。

checkChessboard()

bool cv::checkChessboard	(	InputArray	img,
		Size	size )

Python
	cv.checkChessboard(	img, size	) ->	retval

#include <opencv2/calib3d.hpp>

composeRT()

void cv::composeRT	(	InputArray	第一个旋转向量。,
		InputArray	第一个平移向量。,
		InputArray	第二个旋转向量。,
		InputArray	第二个平移向量。,
		OutputArray	叠加后的输出旋转向量。,
		OutputArray	叠加后的输出平移向量。,
		OutputArray	dr3dr1 = noArray(),
		OutputArray	dr3dt1 = noArray(),
		OutputArray	dr3dr2 = noArray(),
		OutputArray	dr3dt2 = noArray(),
		OutputArray	dt3dr1 = noArray(),
		OutputArray	dt3dt1 = noArray(),
		OutputArray	dt3dr2 = noArray(),
		OutputArray	dt3dt2 = noArray() )

Python
	cv.composeRT(	rvec1, tvec1, rvec2, tvec2[, rvec3[, tvec3[, dr3dr1[, dr3dt1[, dr3dr2[, dr3dt2[, dt3dr1[, dt3dt1[, dt3dr2[, dt3dt2]]]]]]]]]]	) ->	rvec3, tvec3, dr3dr1, dr3dt1, dr3dr2, dr3dt2, dt3dr1, dt3dt1, dt3dr2, dt3dt2

#include <opencv2/calib3d.hpp>

组合两个旋转平移变换。

参数

第一个旋转向量。	第一个旋转向量。
第一个平移向量。	第一个平移向量。
第二个旋转向量。	第二个旋转向量。
第二个平移向量。	第二个平移向量。
叠加后的输出旋转向量。	叠加后的输出旋转向量。
叠加后的输出平移向量。	叠加后的输出平移向量。
dr3dr1	rvec3相对于rvec1的可选输出导数
dr3dt1	rvec3相对于tvec1的可选输出导数
dr3dr2	rvec3相对于rvec2的可选输出导数
dr3dt2	rvec3相对于tvec2的可选输出导数
dt3dr1	tvec3相对于rvec1的可选输出导数
dt3dt1	tvec3相对于tvec1的可选输出导数
dt3dr2	tvec3相对于rvec2的可选输出导数
dt3dt2	tvec3相对于tvec2的可选输出导数

该函数计算

\[\begin{array}{l} \texttt{rvec3} = \mathrm{rodrigues} ^{-1} \left ( \mathrm{rodrigues} ( \texttt{rvec2} ) \cdot \mathrm{rodrigues} ( \texttt{rvec1} ) \right ) \\ \texttt{tvec3} = \mathrm{rodrigues} ( \texttt{rvec2} ) \cdot \texttt{tvec1} + \texttt{tvec2} \end{array} ,\]

其中\(\mathrm{rodrigues}\)表示从旋转向量到旋转矩阵的变换，\(\mathrm{rodrigues}^{-1}\)表示逆变换。详情参见Rodrigues。

此外，该函数可以计算输出向量相对于输入向量的导数（参见matMulDeriv）。该函数在stereoCalibrate内部使用，但也可用于您自己的代码中，当使用Levenberg-Marquardt或其他基于梯度的求解器优化包含矩阵乘法的函数时。

computeCorrespondEpilines()

void cv::computeCorrespondEpilines	(	InputArray	输入点。CV_32FC2类型的\(N \times 1\)或\(1 \times N\)矩阵，或vector<Point2f>。,
		int	包含这些点的图像索引（1或2）。,
		InputArray	基本矩阵，可以使用findFundamentalMat或stereoRectify进行估计。,
		OutputArray	lines )

Python
	cv.computeCorrespondEpilines(	points, whichImage, F[, lines]	) ->	输出向量，包含与另一图像中点对应的对极线。每条线\(ax + by + c=0\)由3个数字\((a, b, c)\)编码。

#include <opencv2/calib3d.hpp>

对于立体对图像中的点，计算另一图像中的对应对极线。

参数

输入点。CV_32FC2类型的\(N \times 1\)或\(1 \times N\)矩阵，或vector<Point2f>。	输入点。CV_32FC2类型的\(N \times 1\)或\(1 \times N\)矩阵，或vector<Point2f>。
包含这些点的图像索引（1或2）。	包含这些点的图像索引（1或2）。
基本矩阵，可以使用findFundamentalMat或stereoRectify进行估计。	基本矩阵，可以使用findFundamentalMat或stereoRectify进行估计。
输出向量，包含与另一图像中点对应的对极线。每条线\(ax + by + c=0\)由3个数字\((a, b, c)\)编码。	输出向量，包含与另一图像中点对应的对极线。每条线\(ax + by + c=0\)由3个数字\((a, b, c)\)编码。

对于立体图像对中其中一张图像的每个点，该函数会找到另一张图像中对应对极线的方程。

根据基本矩阵的定义（参见findFundamentalMat），当whichImage=1时，第二张图像中点\(p^{(1)}_i\)对应的对极线\(l^{(2)}_i\)计算如下：

\[l^{(2)}_i = F p^{(1)}_i\]

反之，当whichImage=2时，\(l^{(1)}_i\)由\(p^{(2)}_i\)计算如下：

\[l^{(1)}_i = F^T p^{(2)}_i\]

直线系数在一定尺度下定义。它们被归一化，使得\(a_i^2+b_i^2=1\)。

convertPointsFromHomogeneous()

void cv::convertPointsFromHomogeneous	(	InputArray	src,
		OutputArray	dst )

Python
	cv.convertPointsFromHomogeneous(	src[, dst]	) ->	dst

#include <opencv2/calib3d.hpp>

将点从齐次坐标空间转换为欧几里得空间。

参数

src	输入N维点向量。
dst	输出N-1维点向量。

该函数使用透视投影将齐次坐标点转换为欧几里得空间点。也就是说，每个点(x1, x2, ... x(n-1), xn)被转换为(x1/xn, x2/xn, ..., x(n-1)/xn)。当xn=0时，输出点坐标将为(0,0,0,...)。

convertPointsHomogeneous()

void cv::convertPointsHomogeneous	(	InputArray	src,
		OutputArray	dst )

#include <opencv2/calib3d.hpp>

将点转换为齐次坐标或从齐次坐标转换。

参数

src	输入2D、3D或4D点数组或向量。
dst	输出2D、3D或4D点向量。

该函数通过调用convertPointsToHomogeneous或convertPointsFromHomogeneous来转换2D或3D点在齐次坐标与欧几里得坐标之间。

注意

此函数已过时。请改用前两个函数之一。

convertPointsToHomogeneous()

void cv::convertPointsToHomogeneous	(	InputArray	src,
		OutputArray	dst )

Python
	cv.convertPointsToHomogeneous(	src[, dst]	) ->	dst

#include <opencv2/calib3d.hpp>

将点从欧几里得空间转换为齐次空间。

参数

src	输入N维点向量。
dst	输出N+1维点向量。

该函数通过在点坐标元组后附加1来将欧几里得空间点转换为齐次空间点。也就是说，每个点(x1, x2, ..., xn)被转换为(x1, x2, ..., xn, 1)。

correctMatches()

void cv::correctMatches	(	InputArray	基本矩阵，可以使用findFundamentalMat或stereoRectify进行估计。,
		InputArray	3x3基本矩阵。,
		InputArray	包含第一组点的1xN数组。,
		OutputArray	包含第二组点的1xN数组。,
		OutputArray	newPoints2 )

Python
	cv.correctMatches(	F, points1, points2[, newPoints1[, newPoints2]]	) ->	优化后的points1。

#include <opencv2/calib3d.hpp>

细化对应点的坐标。

参数

基本矩阵，可以使用findFundamentalMat或stereoRectify进行估计。	3x3基本矩阵。
3x3基本矩阵。	包含第一组点的1xN数组。
包含第一组点的1xN数组。	包含第二组点的1xN数组。
包含第二组点的1xN数组。	优化后的points1。
newPoints2	优化后的points2。

该函数实现了最优三角测量方法（详情参见《多视图几何》[119]）。对于每对给定的点对应关系points1[i] <-> points2[i]以及基本矩阵F，它计算校正后的对应关系newPoints1[i] <-> newPoints2[i]，以最小化几何误差\(d(points1[i], newPoints1[i])^2 + d(points2[i],newPoints2[i])^2\)（其中\(d(a,b)\)是点\(a\)和\(b\)之间的几何距离），同时满足对极约束\(newPoints2^T \cdot F \cdot newPoints1 = 0\)。

decomposeEssentialMat()

void cv::decomposeEssentialMat	(	InputArray	输入的本质矩阵。,
		OutputArray	一个可能的旋转矩阵。,
		OutputArray	另一个可能的旋转矩阵。,
		OutputArray	t )

Python
	cv.decomposeEssentialMat(	E[, R1[, R2[, t]]]	) ->	R1, R2, t

#include <opencv2/calib3d.hpp>

将本征矩阵分解为可能的旋转和平移。

参数

输入的本质矩阵。	输入的本质矩阵。
一个可能的旋转矩阵。	一个可能的旋转矩阵。
另一个可能的旋转矩阵。	另一个可能的旋转矩阵。
t	一个可能的平移向量。

该函数使用SVD分解[119]分解本质矩阵E。通常，E的分解存在四种可能的姿态，分别是\([R_1, t]\)、\([R_1, -t]\)、\([R_2, t]\)、\([R_2, -t]\)。

如果E在第一张图像中的图像点\(p_1\)和第二张图像中的图像点\(p_2\)之间给出对极约束\([p_2; 1]^T A^{-T} E A^{-1} [p_1; 1] = 0\)，那么元组\([R_1, t]\)、\([R_1, -t]\)、\([R_2, t]\)、\([R_2, -t]\)中的任何一个都是从第一个相机的坐标系到第二个相机的坐标系的基变换。然而，通过分解E，只能得到平移的方向。因此，平移t以单位长度返回。

decomposeHomographyMat()

int cv::decomposeHomographyMat	(	InputArray	两图像之间的输入单应矩阵。,
		InputArray	输入的相机内参矩阵。,
		OutputArrayOfArrays	旋转矩阵数组。,
		OutputArrayOfArrays	平移矩阵数组。,
		OutputArrayOfArrays	normals )

Python
	cv.decomposeHomographyMat(	H, K[, rotations[, translations[, normals]]]	) ->	retval, rotations, translations, normals

#include <opencv2/calib3d.hpp>

将单应性矩阵分解为旋转、平移和平面法线。

参数

两图像之间的输入单应矩阵。	两图像之间的输入单应矩阵。
输入的相机内参矩阵。	输入的相机内参矩阵。
旋转矩阵数组。	旋转矩阵数组。
平移矩阵数组。	平移矩阵数组。
normals	平面法线矩阵数组。

该函数提取平面物体两视图之间的相对相机运动，并返回至多四个旋转、平移和平面法线的数学解元组。单应矩阵H的分解在[183]中详细描述。

如果由平面引起的单应H给出约束

\[s_i \vecthree{x'_i}{y'_i}{1} \sim H \vecthree{x_i}{y_i}{1}\]

在源图像点\(p_i\)和目标图像点\(p'_i\)上，则旋转[k]和平移[k]的元组是从源相机的坐标系到目标相机的坐标系的基变换。然而，通过分解H，只能得到按场景（通常未知）深度归一化的平移，即其方向但长度已归一化。

如果存在点对应关系，至少两个解可以通过应用正深度约束（即所有点必须在相机前方）进一步失效。

decomposeProjectionMatrix()

void cv::decomposeProjectionMatrix	(	InputArray	3x4输入投影矩阵P。,
		OutputArray	cameraMatrix,
		OutputArray	输出3x3相机内参矩阵\(\cameramatrix{A}\)。,
		OutputArray	输出3x3外部旋转矩阵R。,
		OutputArray	rotMatrixX = noArray(),
		OutputArray	rotMatrixY = noArray(),
		OutputArray	rotMatrixZ = noArray(),
		OutputArray	eulerAngles = noArray() )

Python
	cv.decomposeProjectionMatrix(	projMatrix[, cameraMatrix[, rotMatrix[, transVect[, rotMatrixX[, rotMatrixY[, rotMatrixZ[, eulerAngles]]]]]]]	) ->	cameraMatrix, rotMatrix, transVect, rotMatrixX, rotMatrixY, rotMatrixZ, eulerAngles

#include <opencv2/calib3d.hpp>

将投影矩阵分解为旋转矩阵和相机内参矩阵。

参数

3x4输入投影矩阵P。	3x4输入投影矩阵P。
cameraMatrix	输出3x3相机内参矩阵\(\cameramatrix{A}\)。
输出3x3相机内参矩阵\(\cameramatrix{A}\)。	输出3x3外部旋转矩阵R。
输出3x3外部旋转矩阵R。	输出4x1平移向量T。
rotMatrixX	可选的绕X轴的3x3旋转矩阵。
rotMatrixY	可选的绕Y轴的3x3旋转矩阵。
rotMatrixZ	可选的绕Z轴的3x3旋转矩阵。
eulerAngles	可选的三元素向量，包含三个欧拉旋转角度（度）。

该函数计算投影矩阵分解为标定矩阵、旋转矩阵和相机位置。

它可选地返回三个旋转矩阵，每个轴一个，以及可在OpenGL中使用的三个欧拉角。请注意，关于三个主轴的旋转序列不止一种，它们可以产生物体的相同方向，例如参见[251]。返回的三个旋转矩阵和相应的三个欧拉角只是可能的解决方案之一。

该函数基于RQDecomp3x3。

drawChessboardCorners()

void cv::drawChessboardCorners	(	InputOutputArray	image,
		Size	每行和每列棋盘格内部角点的数量（patternSize = cv::Size(points_per_row,points_per_column)）。,
		InputArray	检测到的角点数组，findChessboardCorners的输出。,
		bool	patternWasFound )

Python
	cv.drawChessboardCorners(	image, patternSize, corners, patternWasFound	) ->	image

#include <opencv2/calib3d.hpp>

渲染检测到的棋盘角点。

参数

image	目标图像。必须是8位彩色图像。
每行和每列棋盘格内部角点的数量（patternSize = cv::Size(points_per_row,points_per_column)）。	每行和每列棋盘格内部角点的数量（patternSize = cv::Size(points_per_row,points_per_column)）。
检测到的角点数组，findChessboardCorners的输出。	检测到的角点数组，findChessboardCorners的输出。
patternWasFound	指示是否找到完整棋盘格的参数。findChessboardCorners的返回值应在此处传递。

如果未找到棋盘格，该函数将检测到的单个棋盘格角点绘制为红色圆圈；如果找到棋盘格，则绘制为用线条连接的彩色角点。

drawFrameAxes()

void cv::drawFrameAxes	(	InputOutputArray	image,
		InputArray	cameraMatrix,
		InputArray	distCoeffs,
		InputArray	rvec,
		InputArray	tvec,
		float	绘制轴的长度，单位与tvec相同（通常为米）。,
		int	thickness = 3 )

Python
	cv.drawFrameAxes(	image, cameraMatrix, distCoeffs, rvec, tvec, length[, thickness]	) ->	image

#include <opencv2/calib3d.hpp>

从姿态估计中绘制世界/物体坐标系的轴。

另请参见

solvePnP

参数

image	输入/输出图像。必须有1个或3个通道。通道数不变。
cameraMatrix	输入3x3浮点相机内参矩阵。\(\cameramatrix{A}\)
distCoeffs	输入畸变系数向量\(\distcoeffs\)。如果向量为空，则假定畸变系数为零。
rvec	旋转向量（参见Rodrigues），与tvec一起将点从模型坐标系转换到相机坐标系。
tvec	平移向量。
绘制轴的长度，单位与tvec相同（通常为米）。	绘制轴的长度，单位与tvec相同（通常为米）。
thickness	绘制轴的线宽。

该函数绘制世界/物体坐标系相对于相机坐标系的轴。OX轴用红色绘制，OY轴用绿色绘制，OZ轴用蓝色绘制。

estimateAffine2D() [1/2]

cv::Mat cv::estimateAffine2D	(	InputArray	第一个输入2D点集，包含\((X,Y)\)。,
		InputArray	第二个输入2D点集，包含\((x,y)\)。,
		OutputArray	inliers = noArray(),
		int	method = RANSAC,
		double	ransacReprojThreshold = 3,
		size_t	maxIters = 2000,
		double	confidence = 0.99,
		size_t	refineIters = 10 )

Python
	cv.estimateAffine2D(	from_, to[, inliers[, method[, ransacReprojThreshold[, maxIters[, confidence[, refineIters]]]]]]	) ->	retval, inliers
	cv.estimateAffine2D(	pts1, pts2, params[, inliers]	) ->	retval, inliers

#include <opencv2/calib3d.hpp>

计算两个二维点集之间的最优仿射变换。

它计算

\[ \begin{bmatrix} x\\ y\\ \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12}\\ a_{21} & a_{22}\\ \end{bmatrix} \begin{bmatrix} X\\ Y\\ \end{bmatrix} + \begin{bmatrix} b_1\\ b_2\\ \end{bmatrix} \]

参数

第一个输入2D点集，包含\((X,Y)\)。	第一个输入2D点集，包含\((X,Y)\)。
第二个输入2D点集，包含\((x,y)\)。	第二个输入2D点集，包含\((x,y)\)。
inliers	输出向量，指示哪些点是内点（1-内点，0-外点）。
方法	用于计算变换的鲁棒方法。可能的方法如下 RANSAC - 基于RANSAC的鲁棒方法 LMEDS - 最小中值鲁棒方法。RANSAC是默认方法。
ransacReprojThreshold	RANSAC算法中用于将点视为内点的最大重投影误差。仅适用于RANSAC。
maxIters	鲁棒方法的最大迭代次数。
confidence	估计变换的置信水平，介于0和1之间。通常0.95到0.99之间即可。过接近1的值可能会显著减慢估计速度。低于0.8-0.9的值可能导致不正确的变换估计。
refineIters	精炼算法（Levenberg-Marquardt）的最大迭代次数。传递0将禁用精炼，因此输出矩阵将是鲁棒方法的输出。

返回

输出2D仿射变换矩阵，尺寸为\(2 \times 3\)，如果无法估计变换则为空矩阵。返回的矩阵形式如下：

\[ \begin{bmatrix} a_{11} & a_{12} & b_1\\ a_{21} & a_{22} & b_2\\ \end{bmatrix} \]

该函数使用所选的鲁棒算法估计两个2D点集之间的最优2D仿射变换。

然后，使用Levenberg-Marquardt方法对计算出的变换进行进一步精炼（仅使用内点），以进一步减小重投影误差。

注意

RANSAC方法几乎可以处理任何比例的异常值，但需要一个阈值来区分内点和异常值。LMeDS方法不需要任何阈值，但它仅在内点数量超过50%时才能正确工作。

另请参见

estimateAffinePartial2D, getAffineTransform

estimateAffine2D() [2/2]

cv::Mat cv::estimateAffine2D	(	InputArray	pts1,
		InputArray	pts2,
		OutputArray	inliers,
		const UsacParams &	params )

Python
	cv.estimateAffine2D(	from_, to[, inliers[, method[, ransacReprojThreshold[, maxIters[, confidence[, refineIters]]]]]]	) ->	retval, inliers
	cv.estimateAffine2D(	pts1, pts2, params[, inliers]	) ->	retval, inliers

#include <opencv2/calib3d.hpp>

estimateAffine3D() [1/2]

cv::Mat cv::estimateAffine3D	(	InputArray	src,
		InputArray	dst,
		如果传入NULL，则假定尺度参数c为1.0。否则，指向的变量将被设置为最优尺度。	scale = nullptr,
		bool	force_rotation = true )

Python
	cv.estimateAffine3D(	src, dst[, out[, inliers[, ransacThreshold[, confidence]]]]	) ->	retval, out, inliers
	cv.estimateAffine3D(	src, dst[, force_rotation]	) ->	retval, scale

#include <opencv2/calib3d.hpp>

计算两个三维点集之间的最优仿射变换。

它计算最小化\(\sum{i} dst_i - c \cdot R \cdot src_i \)的\(R,s,t\)，其中\(R\)是3x3旋转矩阵，\(t\)是3x1平移向量，\(s\)是标量尺寸值。这是Umeyama算法[281]的实现。估计的仿射变换具有齐次尺度，它是具有7个自由度的仿射变换的子类。配对的点集每个至少需要包含3个点。

参数

src	第一个输入3D点集。
dst	第二个输入3D点集。
scale	如果传入NULL，则假定尺度参数c为1.0。否则，指向的变量将被设置为最优尺度。
force_rotation	如果为true，返回的旋转永远不会是反射。这可能是非期望的，例如在优化右旋和左旋坐标系之间的变换时。

返回

形式为\(3 \times 4\)的3D仿射变换矩阵

\[T = \begin{bmatrix} R & t\\ \end{bmatrix} \]

estimateAffine3D() [2/2]

int cv::estimateAffine3D	(	InputArray	src,
		InputArray	dst,
		OutputArray	输出3D仿射变换矩阵，尺寸为\(3 \times 4\)，形式如下,
		OutputArray	inliers,
		double	ransacThreshold = 3,
		double	confidence = 0.99 )

Python
	cv.estimateAffine3D(	src, dst[, out[, inliers[, ransacThreshold[, confidence]]]]	) ->	retval, out, inliers
	cv.estimateAffine3D(	src, dst[, force_rotation]	) ->	retval, scale

#include <opencv2/calib3d.hpp>

计算两个三维点集之间的最优仿射变换。

它计算

\[ \begin{bmatrix} x\\ y\\ z\\ \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{bmatrix} \begin{bmatrix} X\\ Y\\ Z\\ \end{bmatrix} + \begin{bmatrix} b_1\\ b_2\\ b_3\\ \end{bmatrix} \]

参数

src	第一个输入3D点集，包含\((X,Y,Z)\)。
dst	第二个输入3D点集，包含\((x,y,z)\)。
输出3D仿射变换矩阵，尺寸为\(3 \times 4\)，形式如下	输出形式为\(3 \times 4\)的3D仿射变换矩阵 \[ \begin{bmatrix} a_{11} & a_{12} & a_{13} & b_1\\ a_{21} & a_{22} & a_{23} & b_2\\ a_{31} & a_{32} & a_{33} & b_3\\ \end{bmatrix} \]
inliers	输出向量，指示哪些点是内点（1-内点，0-外点）。
ransacThreshold	RANSAC算法中用于将点视为内点的最大重投影误差。
confidence	估计变换的置信水平，介于0和1之间。通常0.95到0.99之间即可。过接近1的值可能会显著减慢估计速度。低于0.8-0.9的值可能导致不正确的变换估计。

该函数使用RANSAC算法估计两个3D点集之间的最优3D仿射变换。

estimateAffinePartial2D()

cv::Mat cv::estimateAffinePartial2D	(	InputArray	第一个输入2D点集，包含\((X,Y)\)。,
		InputArray	第二个输入2D点集，包含\((x,y)\)。,
		OutputArray	inliers = noArray(),
		int	method = RANSAC,
		double	ransacReprojThreshold = 3,
		size_t	maxIters = 2000,
		double	confidence = 0.99,
		size_t	refineIters = 10 )

Python
	cv.estimateAffinePartial2D(	from_, to[, inliers[, method[, ransacReprojThreshold[, maxIters[, confidence[, refineIters]]]]]]	) ->	retval, inliers

#include <opencv2/calib3d.hpp>

计算两个二维点集之间具有4个自由度的最优受限仿射变换。

参数

第一个输入2D点集，包含\((X,Y)\)。	第一个输入2D点集。
第二个输入2D点集，包含\((x,y)\)。	第二个输入2D点集。
inliers	输出向量，指示哪些点是内点。
方法	用于计算变换的鲁棒方法。可能的方法如下 RANSAC - 基于RANSAC的鲁棒方法 LMEDS - 最小中值鲁棒方法。RANSAC是默认方法。
ransacReprojThreshold	RANSAC算法中用于将点视为内点的最大重投影误差。仅适用于RANSAC。
maxIters	鲁棒方法的最大迭代次数。
confidence	估计变换的置信水平，介于0和1之间。通常0.95到0.99之间即可。过接近1的值可能会显著减慢估计速度。低于0.8-0.9的值可能导致不正确的变换估计。
refineIters	精炼算法（Levenberg-Marquardt）的最大迭代次数。传递0将禁用精炼，因此输出矩阵将是鲁棒方法的输出。

返回

输出2D仿射变换（4个自由度）矩阵，尺寸为\(2 \times 3\)，如果无法估计变换则为空矩阵。

该函数使用所选的鲁棒估计算法，估计一个最优的2D仿射变换，该变换具有4个自由度，且仅限于平移、旋转和均匀缩放的组合。

然后，使用Levenberg-Marquardt方法对计算出的变换进行进一步精炼（仅使用内点），以进一步减小重投影误差。

估计的变换矩阵为

\[ \begin{bmatrix} \cos(\theta) \cdot s & -\sin(\theta) \cdot s & t_x \\ \sin(\theta) \cdot s & \cos(\theta) \cdot s & t_y \end{bmatrix} \]

其中\( \theta \)是旋转角度，\( s \)是缩放因子，\( t_x, t_y \)分别是X轴和Y轴上的平移量。

注意

RANSAC方法几乎可以处理任何比例的异常值，但需要一个阈值来区分内点和异常值。LMeDS方法不需要任何阈值，但它仅在内点数量超过50%时才能正确工作。

另请参见

estimateAffine2D, getAffineTransform

estimateChessboardSharpness()

Scalar cv::estimateChessboardSharpness	(	InputArray	image,
		Size	每行和每列棋盘格内部角点的数量（patternSize = cv::Size(points_per_row,points_per_column)）。,
		InputArray	检测到的角点数组，findChessboardCorners的输出。,
		float	rise_distance = 0.8F,
		bool	vertical = false,
		OutputArray	sharpness = noArray() )

Python
	cv.estimateChessboardSharpness(	image, patternSize, corners[, rise_distance[, vertical[, sharpness]]]	) ->	retval, sharpness

#include <opencv2/calib3d.hpp>

估计检测到的棋盘的清晰度。

图像锐度以及亮度是精确相机标定的关键参数。为了访问这些参数以滤除有问题的标定图像，此方法通过从黑到白棋盘格单元中心遍历来计算边缘轮廓。基于此，计算从黑到白过渡所需的像素数。此过渡区域的宽度是棋盘格成像锐度的一个良好指示，应低于约3.0像素。

参数

image	用于查找棋盘格角点的灰度图像
每行和每列棋盘格内部角点的数量（patternSize = cv::Size(points_per_row,points_per_column)）。	找到的棋盘格图案大小
检测到的角点数组，findChessboardCorners的输出。	通过findChessboardCornersSB找到的角点
rise_distance	上升距离，0.8表示最终信号强度的10%...90%。
vertical	默认情况下计算水平线的边缘响应
sharpness	可选的输出数组，包含计算出的边缘响应的锐度值（参见描述）

可选的锐度数组类型为CV_32FC1，每个计算出的轮廓有一行，包含以下五个条目：0 = 图像中底层边缘的X坐标 1 = 图像中底层边缘的Y坐标 2 = 过渡区域的宽度（锐度） 3 = 黑色单元格中的信号强度（最小亮度） 4 = 白色单元格中的信号强度（最大亮度）

返回

Scalar(平均锐度, 平均最小亮度, 平均最大亮度, 0)

estimateTranslation3D()

int cv::estimateTranslation3D	(	InputArray	src,
		InputArray	dst,
		OutputArray	输出3D仿射变换矩阵，尺寸为\(3 \times 4\)，形式如下,
		OutputArray	inliers,
		double	ransacThreshold = 3,
		double	confidence = 0.99 )

Python
	cv.estimateTranslation3D(	src, dst[, out[, inliers[, ransacThreshold[, confidence]]]]	) ->	retval, out, inliers

#include <opencv2/calib3d.hpp>

计算两个三维点集之间的最优平移。

它计算

\[ \begin{bmatrix} x\\ y\\ z\\ \end{bmatrix} = \begin{bmatrix} X\\ Y\\ Z\\ \end{bmatrix} + \begin{bmatrix} b_1\\ b_2\\ b_3\\ \end{bmatrix} \]

参数

src	第一个输入3D点集，包含\((X,Y,Z)\)。
dst	第二个输入3D点集，包含\((x,y,z)\)。
输出3D仿射变换矩阵，尺寸为\(3 \times 4\)，形式如下	输出形式为\(3 \times 1\)的3D平移向量 \[ \begin{bmatrix} b_1 \\ b_2 \\ b_3 \\ \end{bmatrix} \]
inliers	输出向量，指示哪些点是内点（1-内点，0-外点）。
ransacThreshold	RANSAC算法中用于将点视为内点的最大重投影误差。
confidence	估计变换的置信水平，介于0和1之间。通常0.95到0.99之间即可。过接近1的值可能会显著减慢估计速度。低于0.8-0.9的值可能导致不正确的变换估计。

该函数使用RANSAC算法估计两个3D点集之间的最优3D平移。

filterHomographyDecompByVisibleRefpoints()

void cv::filterHomographyDecompByVisibleRefpoints	(	InputArrayOfArrays	旋转矩阵数组。,
		InputArrayOfArrays	normals,
		InputArray	旋转矩阵向量。,
		InputArray	平面法线矩阵向量。,
		OutputArray	应用单应变换前（校正后）可见参考点的向量,
		InputArray	pointsMask = noArray() )

Python
	cv.filterHomographyDecompByVisibleRefpoints(	rotations, normals, beforePoints, afterPoints[, possibleSolutions[, pointsMask]]	) ->	应用单应变换前（校正后）可见参考点的向量

#include <opencv2/calib3d.hpp>

根据附加信息过滤单应性分解。

参数

旋转矩阵数组。	旋转矩阵向量。
normals	平面法线矩阵向量。
旋转矩阵向量。	应用单应变换前（校正后）可见参考点的向量
平面法线矩阵向量。	应用单应变换后（校正后）可见参考点的向量
应用单应变换前（校正后）可见参考点的向量	过滤后表示可行解集的int索引向量
pointsMask	可选的Mat/Vector，8u类型，表示由findHomography函数给出的内点掩码

此函数旨在根据[183]中描述的附加信息过滤decomposeHomographyMat的输出。方法总结：decomposeHomographyMat函数返回2个独特的解决方案及其“相反”的解决方案，总共有4个解决方案。如果我们能够访问在应用单应变换前后在相机坐标系中可见的点集，我们可以通过验证哪些单应性与所有可见参考点都在相机前方一致来确定哪些是真正的潜在解决方案以及哪些是相反的解决方案。输入保持不变；过滤后的解决方案集作为现有解决方案的索引返回。

filterSpeckles()

void cv::filterSpeckles	(	InputOutputArray	img,
		double	用于涂抹斑点的视差值,
		int	要被视为斑点的最大斑点大小。较大的斑点不受算法影响,
		double	相邻视差像素之间的最大差异，以便将它们放入同一斑点中。请注意，由于StereoBM、StereoSGBM以及可能其他算法返回定点视差图（其中视差值乘以16），因此在指定此参数值时应考虑此比例因子。,
		InputOutputArray	buf = noArray() )

Python
	cv.filterSpeckles(	img, newVal, maxSpeckleSize, maxDiff[, buf]	) ->	img, buf

#include <opencv2/calib3d.hpp>

过滤视差图中小的噪声斑点。

参数

img	输入16位有符号视差图像
用于涂抹斑点的视差值	用于涂抹斑点的视差值
要被视为斑点的最大斑点大小。较大的斑点不受算法影响	要被视为斑点的最大斑点大小。较大的斑点不受算法影响。
相邻视差像素之间的最大差异，以便将它们放入同一斑点中。请注意，由于StereoBM、StereoSGBM以及可能其他算法返回定点视差图（其中视差值乘以16），因此在指定此参数值时应考虑此比例因子。	相邻视差像素之间的最大差异，以便将它们放入同一斑点中。请注意，由于StereoBM、StereoSGBM以及可能其他算法返回定点视差图（其中视差值乘以16），因此在指定此参数值时应考虑此比例因子。
buf	可选的临时缓冲区，用于避免函数内部的内存分配。

find4QuadCornerSubpix()

bool cv::find4QuadCornerSubpix	(	InputArray	img,
		InputOutputArray	检测到的角点数组，findChessboardCorners的输出。,
		Size	region_size )

Python
	cv.find4QuadCornerSubpix(	img, corners, region_size	) ->	retval, corners

#include <opencv2/calib3d.hpp>

查找棋盘角点的亚像素精确位置

findChessboardCorners()

bool cv::findChessboardCorners	(	InputArray	image,
		Size	每行和每列棋盘格内部角点的数量（patternSize = cv::Size(points_per_row,points_per_column)）。,
		OutputArray	检测到的角点数组，findChessboardCorners的输出。,
		int	flags = CALIB_CB_ADAPTIVE_THRESH+CALIB_CB_NORMALIZE_IMAGE )

Python
	cv.findChessboardCorners(	image, patternSize[, corners[, flags]]	) ->	retval, corners

#include <opencv2/calib3d.hpp>

查找棋盘内部角点的位置。

参数

image	源棋盘格视图。必须是8位灰度或彩色图像。
每行和每列棋盘格内部角点的数量（patternSize = cv::Size(points_per_row,points_per_column)）。	每行和每列棋盘格内部角点的数量（ patternSize = cv::Size(points_per_row,points_per_colum) = cv::Size(columns,rows)）。
检测到的角点数组，findChessboardCorners的输出。	输出检测到的角点数组。
flags	各种操作标志，可以是零或以下值的组合 CALIB_CB_ADAPTIVE_THRESH 使用自适应阈值将图像转换为黑白图像，而不是固定的阈值水平（从平均图像亮度计算）。 CALIB_CB_NORMALIZE_IMAGE 在应用固定或自适应阈值之前，使用equalizeHist对图像伽马进行归一化。 CALIB_CB_FILTER_QUADS 使用附加标准（如轮廓面积、周长、类方形形状）过滤掉在轮廓检索阶段提取的错误四边形。 CALIB_CB_FAST_CHECK 对图像进行快速检查，查找棋盘格角点，如果未找到则提前返回。这可以在未观察到棋盘格的退化情况下大大加快调用速度。 CALIB_CB_PLAIN 忽略所有其他标志。输入图像按原样处理。不进行图像处理以改进棋盘格的查找。这会加快函数执行速度，但如果图像未事先以适当方式二值化，则可能无法识别棋盘格。

该函数尝试确定输入图像是否为棋盘格图案视图并定位内部棋盘格角点。如果找到所有角点并以特定顺序（逐行，每行从左到右）排列，则该函数返回非零值。否则，如果函数未能找到所有角点或未能重新排序，则返回0。例如，一个普通的棋盘格有8x8个方格和7x7个内部角点，即黑色方格相互接触的点。检测到的坐标是近似的，为了更准确地确定它们的位置，该函数调用cornerSubPix。如果返回的坐标不够精确，您也可以使用不同参数的cornerSubPix函数。

检测和绘制棋盘格角点的示例用法：

Size patternsize(8,6); // 内部角点数量
Mat gray = ....; // 源图像
vector<Point2f> corners; // 这将由检测到的角点填充
 
//CALIB_CB_FAST_CHECK 在不包含任何棋盘格角点的图像上节省大量时间
//（不包含任何棋盘格角点的图像）
bool patternfound = findChessboardCorners(gray, patternsize, corners,
        CALIB_CB_ADAPTIVE_THRESH + CALIB_CB_NORMALIZE_IMAGE
+ CALIB_CB_FAST_CHECK);
 
if(patternfound)
  cornerSubPix(gray, corners, Size(11, 11), Size(-1, -1),
    TermCriteria(CV_TERMCRIT_EPS + CV_TERMCRIT_ITER, 30, 0.1));
 
drawChessboardCorners(img, patternsize, Mat(corners), patternfound);

注意

该函数要求棋盘格周围有白色区域（例如方形厚边框，越宽越好），以便在各种环境中使检测更鲁棒。否则，如果棋盘格没有边框且背景较暗，外部黑色方块无法正确分割，从而导致方块分组和排序算法失败。

使用gen_pattern.py Python脚本（创建标定图案）来创建所需的棋盘格图案。

findChessboardCornersSB() [1/2]

bool cv::findChessboardCornersSB	(	InputArray	image,
		Size	每行和每列棋盘格内部角点的数量（patternSize = cv::Size(points_per_row,points_per_column)）。,
		OutputArray	检测到的角点数组，findChessboardCorners的输出。,
		int	flags,
		OutputArray	meta )

Python
	cv.findChessboardCornersSB(	image, patternSize[, corners[, flags]]	) ->	retval, corners
	cv.findChessboardCornersSBWithMeta(	image, patternSize, flags[, corners[, meta]]	) ->	retval, corners, meta

#include <opencv2/calib3d.hpp>

使用基于扇区的方法查找棋盘内部角点的位置。

参数

image	源棋盘格视图。必须是8位灰度或彩色图像。
每行和每列棋盘格内部角点的数量（patternSize = cv::Size(points_per_row,points_per_column)）。	每行和每列棋盘格内部角点的数量（ patternSize = cv::Size(points_per_row,points_per_colum) = cv::Size(columns,rows)）。
检测到的角点数组，findChessboardCorners的输出。	输出检测到的角点数组。
flags	各种操作标志，可以是零或以下值的组合 CALIB_CB_NORMALIZE_IMAGE 在检测前使用equalizeHist对图像伽马进行归一化。 CALIB_CB_EXHAUSTIVE 运行穷举搜索以提高检测率。 CALIB_CB_ACCURACY 对输入图像进行上采样以提高由于混叠效应引起的亚像素精度。 CALIB_CB_LARGER 检测到的图案允许大于patternSize（参见描述）。 CALIB_CB_MARKER 检测到的图案必须包含标记（参见描述）。如果需要精确的相机标定，应使用此标志。
meta	可选的输出数组，用于检测到的角点（CV_8UC1类型，大小为cv::Size(columns,rows)）。每个条目代表图案的一个角点，可以有以下值之一 0 = 未附加元数据 1 = 黑色单元格的左上角 2 = 白色单元格的左上角 3 = 带有白色标记点的黑色单元格左上角 4 = 带有黑色标记点的白色单元格左上角（有标记时为图案原点，否则为第一个角点）

该函数与findChessboardCorners类似，但使用通过盒式滤波器近似的局部拉东变换，这种方法对各种噪声更鲁棒，在较大图像上更快，并且能够直接返回内部棋盘格角点的亚像素位置。该方法基于论文[76]“用于标定的棋盘格角点的精确检测与定位”，该论文表明返回的亚像素位置比cornerSubPix返回的更准确，从而允许对要求苛刻的应用进行精确的相机标定。

如果给定标志CALIB_CB_LARGER或CALIB_CB_MARKER，结果可以从可选的元数据数组中恢复。这两个标志都有助于使用超出相机视野的标定图案。这些超大图案允许更精确的标定，因为可以利用尽可能靠近图像边缘的角点。为了在所有图像中保持坐标系统的一致性，可以使用可选标记（见下图）将棋盘格的原点移动到黑色圆圈所在的位置。

注意

该函数要求棋盘格周围有一个与棋盘格方块大致相同宽度的白色边框，以改善在各种环境中的检测。此外，由于局部拉东变换，对位于棋盘格外部的方块角点使用圆角是有益的。下图展示了一个为检测优化的示例棋盘格。但是，也可以使用任何其他棋盘格。

使用gen_pattern.py Python脚本（创建标定图案）来创建相应的棋盘格图案

findChessboardCornersSB() [2/2]

bool cv::findChessboardCornersSB ( InputArray image, Size 每行和每列棋盘格内部角点的数量（patternSize = cv::Size(points_per_row,points_per_column)）。, OutputArray 检测到的角点数组，findChessboardCorners的输出。, int flags = 0 )

inline

Python
	cv.findChessboardCornersSB(	image, patternSize[, corners[, flags]]	) ->	retval, corners
	cv.findChessboardCornersSBWithMeta(	image, patternSize, flags[, corners[, meta]]	) ->	retval, corners, meta

#include <opencv2/calib3d.hpp>

这是一个重载的成员函数，为方便起见而提供。它与上述函数的区别仅在于它接受的参数。

此函数的调用图如下

findCirclesGrid() [1/2]

bool cv::findCirclesGrid	(	InputArray	image,
		Size	每行和每列棋盘格内部角点的数量（patternSize = cv::Size(points_per_row,points_per_column)）。,
		OutputArray	输出检测到的中心点数组。,
		int	flags,
		const Ptr< FeatureDetector > &	特征检测器，用于查找光背景上的暗圆等斑点。如果blobDetector为NULL，则image表示Point2f候选数组。,
		const CirclesGridFinderParameters &	parameters )

Python
	cv.findCirclesGrid(	image, patternSize, flags, blobDetector, parameters[, centers]	) ->	retval, centers
	cv.findCirclesGrid(	image, patternSize[, centers[, flags[, blobDetector]]]	) ->	retval, centers

#include <opencv2/calib3d.hpp>

在圆形网格中查找中心。

参数

image	输入圆形网格视图；必须是8位灰度或彩色图像。
每行和每列棋盘格内部角点的数量（patternSize = cv::Size(points_per_row,points_per_column)）。	每行和每列的圆形数量（ patternSize = Size(points_per_row, points_per_colum)）。
输出检测到的中心点数组。	输出检测到的中心点数组。
flags	各种操作标志，可以是以下值之一 CALIB_CB_SYMMETRIC_GRID 使用对称的圆形图案。 CALIB_CB_ASYMMETRIC_GRID 使用非对称的圆形图案。 CALIB_CB_CLUSTERING 使用特殊的网格检测算法。它对透视畸变更鲁棒，但对背景杂波更敏感。
特征检测器，用于查找光背景上的暗圆等斑点。如果blobDetector为NULL，则image表示Point2f候选数组。	特征检测器，用于查找光背景上的暗圆等斑点。如果blobDetector为NULL，则image表示Point2f候选数组。
parameters	用于在网格图案中查找圆形的结构体。

该函数尝试确定输入图像是否包含圆形网格。如果是，则该函数定位圆心。如果所有圆心都已找到并以特定顺序（逐行，每行从左到右）排列，则该函数返回非零值。否则，如果函数未能找到所有角点或未能重新排序，则返回0。

检测和绘制圆形中心点的示例用法：

Size patternsize(7,7); // 中心点数量
Mat gray = ...; // 源图像
vector<Point2f> centers; // 这将由检测到的中心点填充
 
bool patternfound = findCirclesGrid(gray, patternsize, centers);
 
drawChessboardCorners(img, patternsize, Mat(centers), patternfound);

注意

该函数要求棋盘格周围有白色区域（例如方形厚边框，越宽越好），以便在各种环境中使检测更鲁棒。

findCirclesGrid() [2/2]

bool cv::findCirclesGrid	(	InputArray	image,
		Size	每行和每列棋盘格内部角点的数量（patternSize = cv::Size(points_per_row,points_per_column)）。,
		OutputArray	输出检测到的中心点数组。,
		int	flags = CALIB_CB_SYMMETRIC_GRID,
		const Ptr< FeatureDetector > &	blobDetector = SimpleBlobDetector::create() )

Python
	cv.findCirclesGrid(	image, patternSize, flags, blobDetector, parameters[, centers]	) ->	retval, centers
	cv.findCirclesGrid(	image, patternSize[, centers[, flags[, blobDetector]]]	) ->	retval, centers

#include <opencv2/calib3d.hpp>

这是一个重载的成员函数，为方便起见而提供。它与上述函数的区别仅在于它接受的参数。

findEssentialMat() [1/6]

Mat cv::findEssentialMat	(	InputArray	3x3基本矩阵。,
		InputArray	包含第一组点的1xN数组。,
		double	相机焦距。请注意，此函数假设points1和points2是来自具有相同焦距和主点的相机的特征点。,
		Point2d	相机主点。,
		int	方法,
		double	仅用于RANSAC或LMedS方法的参数。它指定了估计矩阵正确的期望置信水平（概率）。,
		double	RANSAC参数。它是点到像素中对极线的最大距离，超过此距离的点将被视为异常值，不用于计算最终的基本矩阵。它可以设置为1-3左右，具体取决于点定位的精度、图像分辨率和图像噪声。,
		OutputArray	mask )

Python
	cv.findEssentialMat(	points1, points2, cameraMatrix[, method[, prob[, threshold[, maxIters[, mask]]]]]	) ->	retval, mask
	cv.findEssentialMat(	points1, points2[, focal[, pp[, method[, prob[, threshold[, maxIters[, mask]]]]]]]	) ->	retval, mask
	cv.findEssentialMat(	points1, points2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2[, method[, prob[, threshold[, mask]]]]	) ->	retval, mask
	cv.findEssentialMat(	points1, points2, cameraMatrix1, cameraMatrix2, dist_coeff1, dist_coeff2, params[, mask]	) ->	retval, mask

#include <opencv2/calib3d.hpp>

这是一个重载的成员函数，为方便起见而提供。它与上述函数的区别仅在于它接受的参数。

findEssentialMat() [2/6]

Mat cv::findEssentialMat	(	InputArray	3x3基本矩阵。,
		InputArray	包含第一组点的1xN数组。,
		double	focal = 1.0,
		Point2d	pp = Point2d(0, 0),
		int	method = RANSAC,
		double	prob = 0.999,
		double	threshold = 1.0,
		int	maxIters = 1000,
		OutputArray	mask = noArray() )

Python
	cv.findEssentialMat(	points1, points2, cameraMatrix[, method[, prob[, threshold[, maxIters[, mask]]]]]	) ->	retval, mask
	cv.findEssentialMat(	points1, points2[, focal[, pp[, method[, prob[, threshold[, maxIters[, mask]]]]]]]	) ->	retval, mask
	cv.findEssentialMat(	points1, points2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2[, method[, prob[, threshold[, mask]]]]	) ->	retval, mask
	cv.findEssentialMat(	points1, points2, cameraMatrix1, cameraMatrix2, dist_coeff1, dist_coeff2, params[, mask]	) ->	retval, mask

#include <opencv2/calib3d.hpp>

这是一个重载的成员函数，为方便起见而提供。它与上述函数的区别仅在于它接受的参数。

参数

3x3基本矩阵。	来自第一张图像的N个（N >= 5）2D点数组。点坐标应为浮点型（单精度或双精度）。
包含第一组点的1xN数组。	第二张图像的点数组，与points1尺寸和格式相同。
相机焦距。请注意，此函数假设points1和points2是来自具有相同焦距和主点的相机的特征点。	相机焦距。请注意，此函数假设points1和points2是来自具有相同焦距和主点的相机的特征点。
相机主点。	相机主点。
方法	计算基本矩阵的方法。 RANSAC 用于RANSAC算法。 LMEDS 用于LMedS算法。
RANSAC参数。它是点到像素中对极线的最大距离，超过此距离的点将被视为异常值，不用于计算最终的基本矩阵。它可以设置为1-3左右，具体取决于点定位的精度、图像分辨率和图像噪声。	RANSAC参数。它是点到像素中对极线的最大距离，超过此距离的点将被视为异常值，不用于计算最终的基本矩阵。它可以设置为1-3左右，具体取决于点定位的精度、图像分辨率和图像噪声。
仅用于RANSAC或LMedS方法的参数。它指定了估计矩阵正确的期望置信水平（概率）。	仅用于RANSAC或LMedS方法的参数。它指定了估计矩阵正确的期望置信水平（概率）。
mask	输出N个元素的数组，其中每个元素对于异常值设置为0，对于其他点设置为1。该数组仅在RANSAC和LMedS方法中计算。
maxIters	鲁棒方法的最大迭代次数。

此函数与上一个函数的不同之处在于，它从焦距和主点计算相机内参矩阵

\[A = \begin{bmatrix} f & 0 & x_{pp} \\ 0 & f & y_{pp} \\ 0 & 0 & 1 \end{bmatrix}\]

findEssentialMat() [3/6]

Mat cv::findEssentialMat	(	InputArray	3x3基本矩阵。,
		InputArray	包含第一组点的1xN数组。,
		InputArray	cameraMatrix,
		int	方法,
		double	仅用于RANSAC或LMedS方法的参数。它指定了估计矩阵正确的期望置信水平（概率）。,
		double	RANSAC参数。它是点到像素中对极线的最大距离，超过此距离的点将被视为异常值，不用于计算最终的基本矩阵。它可以设置为1-3左右，具体取决于点定位的精度、图像分辨率和图像噪声。,
		OutputArray	mask )

Python
	cv.findEssentialMat(	points1, points2, cameraMatrix[, method[, prob[, threshold[, maxIters[, mask]]]]]	) ->	retval, mask
	cv.findEssentialMat(	points1, points2[, focal[, pp[, method[, prob[, threshold[, maxIters[, mask]]]]]]]	) ->	retval, mask
	cv.findEssentialMat(	points1, points2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2[, method[, prob[, threshold[, mask]]]]	) ->	retval, mask
	cv.findEssentialMat(	points1, points2, cameraMatrix1, cameraMatrix2, dist_coeff1, dist_coeff2, params[, mask]	) ->	retval, mask

#include <opencv2/calib3d.hpp>

这是一个重载的成员函数，为方便起见而提供。它与上述函数的区别仅在于它接受的参数。

findEssentialMat() [4/6]

Mat cv::findEssentialMat	(	InputArray	3x3基本矩阵。,
		InputArray	包含第一组点的1xN数组。,
		InputArray	cameraMatrix,
		int	method = RANSAC,
		double	prob = 0.999,
		double	threshold = 1.0,
		int	maxIters = 1000,
		OutputArray	mask = noArray() )

Python
	cv.findEssentialMat(	points1, points2, cameraMatrix[, method[, prob[, threshold[, maxIters[, mask]]]]]	) ->	retval, mask
	cv.findEssentialMat(	points1, points2[, focal[, pp[, method[, prob[, threshold[, maxIters[, mask]]]]]]]	) ->	retval, mask
	cv.findEssentialMat(	points1, points2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2[, method[, prob[, threshold[, mask]]]]	) ->	retval, mask
	cv.findEssentialMat(	points1, points2, cameraMatrix1, cameraMatrix2, dist_coeff1, dist_coeff2, params[, mask]	) ->	retval, mask

#include <opencv2/calib3d.hpp>

从两张图像中的对应点计算本征矩阵。

参数

3x3基本矩阵。	来自第一张图像的N个（N >= 5）2D点数组。点坐标应为浮点型（单精度或双精度）。
包含第一组点的1xN数组。	第二张图像的点数组，与points1尺寸和格式相同。
cameraMatrix	相机内参矩阵\(\cameramatrix{A}\)。请注意，此函数假设points1和points2是来自具有相同相机内参矩阵的相机的特征点。如果此假设不适用于您的用例，请使用另一个函数重载或对两个相机使用P = cv::NoArray()的undistortPoints来将图像点转换为归一化图像坐标，这些坐标对于单位相机内参矩阵是有效的。传递这些坐标时，为此参数传递单位矩阵。
方法	计算本质矩阵的方法。 RANSAC 用于RANSAC算法。 LMEDS 用于LMedS算法。
仅用于RANSAC或LMedS方法的参数。它指定了估计矩阵正确的期望置信水平（概率）。	仅用于RANSAC或LMedS方法的参数。它指定了估计矩阵正确的期望置信水平（概率）。
RANSAC参数。它是点到像素中对极线的最大距离，超过此距离的点将被视为异常值，不用于计算最终的基本矩阵。它可以设置为1-3左右，具体取决于点定位的精度、图像分辨率和图像噪声。	RANSAC参数。它是点到像素中对极线的最大距离，超过此距离的点将被视为异常值，不用于计算最终的基本矩阵。它可以设置为1-3左右，具体取决于点定位的精度、图像分辨率和图像噪声。
mask	输出N个元素的数组，其中每个元素对于异常值设置为0，对于其他点设置为1。该数组仅在RANSAC和LMedS方法中计算。
maxIters	鲁棒方法的最大迭代次数。

该函数基于[211]中的五点算法求解器估计本质矩阵。[255]也相关。对极几何由以下方程描述：

\[[p_2; 1]^T K^{-T} E K^{-1} [p_1; 1] = 0\]

其中\(E\)是本质矩阵，\(p_1\)和\(p_2\)分别是第一张和第二张图像中的对应点。此函数的结果可以进一步传递给decomposeEssentialMat或recoverPose，以恢复相机之间的相对姿态。

findEssentialMat() [5/6]

Mat cv::findEssentialMat	(	InputArray	3x3基本矩阵。,
		InputArray	包含第一组点的1xN数组。,
		InputArray	第一个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。,
		InputArray	第二个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。,
		InputArray	第一个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。,
		InputArray	第二个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。,
		OutputArray	mask,
		const UsacParams &	params )

Python
	cv.findEssentialMat(	points1, points2, cameraMatrix[, method[, prob[, threshold[, maxIters[, mask]]]]]	) ->	retval, mask
	cv.findEssentialMat(	points1, points2[, focal[, pp[, method[, prob[, threshold[, maxIters[, mask]]]]]]]	) ->	retval, mask
	cv.findEssentialMat(	points1, points2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2[, method[, prob[, threshold[, mask]]]]	) ->	retval, mask
	cv.findEssentialMat(	points1, points2, cameraMatrix1, cameraMatrix2, dist_coeff1, dist_coeff2, params[, mask]	) ->	retval, mask

#include <opencv2/calib3d.hpp>

findEssentialMat() [6/6]

Mat cv::findEssentialMat	(	InputArray	3x3基本矩阵。,
		InputArray	包含第一组点的1xN数组。,
		InputArray	第一个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。,
		InputArray	第一个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。,
		InputArray	第二个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。,
		InputArray	第二个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。,
		int	method = RANSAC,
		double	prob = 0.999,
		double	threshold = 1.0,
		OutputArray	mask = noArray() )

Python
	cv.findEssentialMat(	points1, points2, cameraMatrix[, method[, prob[, threshold[, maxIters[, mask]]]]]	) ->	retval, mask
	cv.findEssentialMat(	points1, points2[, focal[, pp[, method[, prob[, threshold[, maxIters[, mask]]]]]]]	) ->	retval, mask
	cv.findEssentialMat(	points1, points2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2[, method[, prob[, threshold[, mask]]]]	) ->	retval, mask
	cv.findEssentialMat(	points1, points2, cameraMatrix1, cameraMatrix2, dist_coeff1, dist_coeff2, params[, mask]	) ->	retval, mask

#include <opencv2/calib3d.hpp>

从两张（可能来自不同相机）图像中的对应点计算本征矩阵。

参数

3x3基本矩阵。	来自第一张图像的N个（N >= 5）2D点数组。点坐标应为浮点型（单精度或双精度）。
包含第一组点的1xN数组。	第二张图像的点数组，与points1尺寸和格式相同。
第一个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。	第一个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。
第二个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。	第二个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。
第一个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。	第一个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。
第二个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。	第二个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。
方法	计算本质矩阵的方法。 RANSAC 用于RANSAC算法。 LMEDS 用于LMedS算法。
仅用于RANSAC或LMedS方法的参数。它指定了估计矩阵正确的期望置信水平（概率）。	仅用于RANSAC或LMedS方法的参数。它指定了估计矩阵正确的期望置信水平（概率）。
RANSAC参数。它是点到像素中对极线的最大距离，超过此距离的点将被视为异常值，不用于计算最终的基本矩阵。它可以设置为1-3左右，具体取决于点定位的精度、图像分辨率和图像噪声。	RANSAC参数。它是点到像素中对极线的最大距离，超过此距离的点将被视为异常值，不用于计算最终的基本矩阵。它可以设置为1-3左右，具体取决于点定位的精度、图像分辨率和图像噪声。
mask	输出N个元素的数组，其中每个元素对于异常值设置为0，对于其他点设置为1。该数组仅在RANSAC和LMedS方法中计算。

该函数基于[211]中的五点算法求解器估计本质矩阵。[255]也相关。对极几何由以下方程描述：

\[[p_2; 1]^T K^{-T} E K^{-1} [p_1; 1] = 0\]

其中\(E\)是本质矩阵，\(p_1\)和\(p_2\)分别是第一张和第二张图像中的对应点。此函数的结果可以进一步传递给decomposeEssentialMat或recoverPose，以恢复相机之间的相对姿态。

findFundamentalMat() [1/4]

Mat cv::findFundamentalMat	(	InputArray	3x3基本矩阵。,
		InputArray	包含第一组点的1xN数组。,
		int	方法,
		double	ransacReprojThreshold,
		double	confidence,
		int	maxIters,
		OutputArray	mask = noArray() )

Python
	cv.findFundamentalMat(	points1, points2, method, ransacReprojThreshold, confidence, maxIters[, mask]	) ->	retval, mask
	cv.findFundamentalMat(	points1, points2[, method[, ransacReprojThreshold[, confidence[, mask]]]]	) ->	retval, mask
	cv.findFundamentalMat(	points1, points2, params[, mask]	) ->	retval, mask

#include <opencv2/calib3d.hpp>

从两张图像中的对应点计算基础矩阵。

参数

	3x3基本矩阵。	来自第一张图像的N个点数组。点坐标应为浮点型（单精度或双精度）。
	包含第一组点的1xN数组。	第二张图像的点数组，与points1尺寸和格式相同。
	方法	计算基本矩阵的方法。 FM_7POINT 用于7点算法。\(N = 7\) FM_8POINT 用于8点算法。\(N \ge 8\) FM_RANSAC 用于RANSAC算法。\(N \ge 8\) FM_LMEDS 用于LMedS算法。\(N \ge 8\)
	ransacReprojThreshold	仅用于RANSAC的参数。它是点到像素中对极线的最大距离，超过此距离的点将被视为异常值，不用于计算最终的基本矩阵。它可以设置为1-3左右，具体取决于点定位的精度、图像分辨率和图像噪声。
	confidence	仅用于RANSAC和LMedS方法的参数。它指定了估计矩阵正确的期望置信水平（概率）。
[输出]	mask	可选的输出掩码
	maxIters	鲁棒方法的最大迭代次数。

对极几何由以下方程描述：

\[[p_2; 1]^T F [p_1; 1] = 0\]

其中 \(F\) 是一个基础矩阵，\(p_1\) 和 \(p_2\) 分别是第一张图像和第二张图像中的对应点。

该函数使用上面列出的四种方法之一计算基础矩阵，并返回找到的基础矩阵。通常只找到一个矩阵。但在7点算法的情况下，该函数最多可以返回3个解决方案（一个 \(9 \times 3\) 矩阵，按顺序存储所有3个矩阵）。

计算出的基础矩阵可以进一步传递给 computeCorrespondEpilines，该函数用于查找与指定点对应的对极线。它也可以传递给 stereoRectifyUncalibrated 来计算校正变换。

// 示例：使用RANSAC算法估计基础矩阵
int point_count = 100;
vector<Point2f> points1(point_count);
vector<Point2f> points2(point_count);
 
// 在这里初始化点...
for( int i = 0; i < point_count; i++ )
{
points1[i] = ...;
points2[i] = ...;
}
 
Mat fundamental_matrix =
 findFundamentalMat(points1, points2, FM_RANSAC, 3, 0.99);

findFundamentalMat() [2/4]

Mat cv::findFundamentalMat	(	InputArray	3x3基本矩阵。,
		InputArray	包含第一组点的1xN数组。,
		int	method = FM_RANSAC,
		double	ransacReprojThreshold = 3.,
		double	confidence = 0.99,
		OutputArray	mask = noArray() )

Python
	cv.findFundamentalMat(	points1, points2, method, ransacReprojThreshold, confidence, maxIters[, mask]	) ->	retval, mask
	cv.findFundamentalMat(	points1, points2[, method[, ransacReprojThreshold[, confidence[, mask]]]]	) ->	retval, mask
	cv.findFundamentalMat(	points1, points2, params[, mask]	) ->	retval, mask

#include <opencv2/calib3d.hpp>

这是一个重载的成员函数，为方便起见而提供。它与上述函数的区别仅在于它接受的参数。

findFundamentalMat() [3/4]

Mat cv::findFundamentalMat	(	InputArray	3x3基本矩阵。,
		InputArray	包含第一组点的1xN数组。,
		OutputArray	mask,
		const UsacParams &	params )

Python
	cv.findFundamentalMat(	points1, points2, method, ransacReprojThreshold, confidence, maxIters[, mask]	) ->	retval, mask
	cv.findFundamentalMat(	points1, points2[, method[, ransacReprojThreshold[, confidence[, mask]]]]	) ->	retval, mask
	cv.findFundamentalMat(	points1, points2, params[, mask]	) ->	retval, mask

#include <opencv2/calib3d.hpp>

findFundamentalMat() [4/4]

Mat cv::findFundamentalMat	(	InputArray	3x3基本矩阵。,
		InputArray	包含第一组点的1xN数组。,
		OutputArray	mask,
		int	method = FM_RANSAC,
		double	ransacReprojThreshold = 3.,
		double	confidence = 0.99 )

Python
	cv.findFundamentalMat(	points1, points2, method, ransacReprojThreshold, confidence, maxIters[, mask]	) ->	retval, mask
	cv.findFundamentalMat(	points1, points2[, method[, ransacReprojThreshold[, confidence[, mask]]]]	) ->	retval, mask
	cv.findFundamentalMat(	points1, points2, params[, mask]	) ->	retval, mask

#include <opencv2/calib3d.hpp>

这是一个重载的成员函数，为方便起见而提供。它与上述函数的区别仅在于它接受的参数。

findHomography() [1/3]

Mat cv::findHomography	(	InputArray	srcPoints,
		InputArray	dstPoints,
		int	method = 0,
		double	ransacReprojThreshold = 3,
		OutputArray	mask = noArray(),
		const int	maxIters = 2000,
		const double	confidence = 0.995 )

Python
	cv.findHomography(	srcPoints, dstPoints[, method[, ransacReprojThreshold[, mask[, maxIters[, confidence]]]]]	) ->	retval, mask
	cv.findHomography(	srcPoints, dstPoints, params[, mask]	) ->	retval, mask

#include <opencv2/calib3d.hpp>

在两个平面之间查找透视变换。

参数

srcPoints	原始平面中点的坐标，CV_32FC2 类型的矩阵或 vector<Point2f>。
dstPoints	目标平面中点的坐标，CV_32FC2 类型的矩阵或 vector<Point2f>。
方法	用于计算单应性矩阵的方法。可能的方法如下： 0 - 使用所有点的常规方法，即最小二乘法 RANSAC - 基于RANSAC的鲁棒方法 LMEDS - 最小中位数鲁棒方法 RHO - 基于PROSAC的鲁棒方法
ransacReprojThreshold	将点对视为内点的最大允许重投影误差（仅用于RANSAC和RHO方法）。也就是说，如果 \[\| \texttt{dstPoints} _i - \texttt{convertPointsHomogeneous} ( \texttt{H} \cdot \texttt{srcPoints} _i) \|_2 > \texttt{ransacReprojThreshold}\] 则点 \(i\) 被视为外点。如果 srcPoints 和 dstPoints 以像素为单位测量，通常将此参数设置在 1 到 10 的范围内比较合理。
mask	由鲁棒方法（RANSAC或LMeDS）设置的可选输出掩码。请注意，输入掩码值将被忽略。
maxIters	RANSAC的最大迭代次数。
confidence	置信度，介于0和1之间。

该函数查找并返回源平面和目标平面之间的透视变换 \(H\)

\[s_i \vecthree{x'_i}{y'_i}{1} \sim H \vecthree{x_i}{y_i}{1}\]

以使反向投影误差

\[\sum _i \left ( x'_i- \frac{h_{11} x_i + h_{12} y_i + h_{13}}{h_{31} x_i + h_{32} y_i + h_{33}} \right )^2+ \left ( y'_i- \frac{h_{21} x_i + h_{22} y_i + h_{23}}{h_{31} x_i + h_{32} y_i + h_{33}} \right )^2\]

最小化。如果参数 method 设置为默认值0，则函数使用所有点对通过简单的最小二乘方案计算初始单应性估计。

然而，如果并非所有点对（ \(srcPoints_i\), \(dstPoints_i\) ）都符合刚性透视变换（即存在一些异常值），则此初始估计将很差。在这种情况下，可以使用三种鲁棒方法之一。RANSAC、LMeDS和RHO方法尝试许多不同的对应点对随机子集（每个子集包含四对，共线对被丢弃），使用此子集和简单的最小二乘算法估计单应性矩阵，然后计算所估计单应性矩阵的质量/优度（RANSAC是内点数量，LMeDS是最小中值重投影误差）。然后，最佳子集用于生成单应性矩阵的初始估计以及内点/外点掩码。

无论是否使用鲁棒方法，计算出的单应性矩阵都会使用Levenberg-Marquardt方法进一步优化（如果使用鲁棒方法，则仅使用内点），以进一步减小重投影误差。

RANSAC和RHO方法可以处理几乎任何比例的异常值，但需要一个阈值来区分内点和异常值。LMeDS方法不需要任何阈值，但它仅在内点超过50%时才能正确工作。最后，如果没有异常值且噪声较小，请使用默认方法（method=0）。

该函数用于查找初始内参和外参矩阵。单应性矩阵是在一个尺度下确定的。如果 \(h_{33}\) 不为零，则将矩阵归一化，使得 \(h_{33}=1\)。

注意

如果无法估计 \(H\) 矩阵，将返回一个空矩阵。

另请参见

getAffineTransform, estimateAffine2D, estimateAffinePartial2D, getPerspectiveTransform, warpPerspective, perspectiveTransform

findHomography() [2/3]

Mat cv::findHomography	(	InputArray	srcPoints,
		InputArray	dstPoints,
		OutputArray	mask,
		const UsacParams &	params )

Python
	cv.findHomography(	srcPoints, dstPoints[, method[, ransacReprojThreshold[, mask[, maxIters[, confidence]]]]]	) ->	retval, mask
	cv.findHomography(	srcPoints, dstPoints, params[, mask]	) ->	retval, mask

#include <opencv2/calib3d.hpp>

findHomography() [3/3]

Mat cv::findHomography	(	InputArray	srcPoints,
		InputArray	dstPoints,
		OutputArray	mask,
		int	method = 0,
		double	ransacReprojThreshold = 3 )

Python
	cv.findHomography(	srcPoints, dstPoints[, method[, ransacReprojThreshold[, mask[, maxIters[, confidence]]]]]	) ->	retval, mask
	cv.findHomography(	srcPoints, dstPoints, params[, mask]	) ->	retval, mask

#include <opencv2/calib3d.hpp>

这是一个重载的成员函数，为方便起见而提供。它与上述函数的区别仅在于它接受的参数。

getDefaultNewCameraMatrix()

Mat cv::getDefaultNewCameraMatrix	(	InputArray	cameraMatrix,
		Size	imgsize = Size(),
		bool	centerPrincipalPoint = false )

Python
	cv.getDefaultNewCameraMatrix(	cameraMatrix[, imgsize[, centerPrincipalPoint]]	) ->	retval

#include <opencv2/calib3d.hpp>

返回默认的新相机矩阵。

该函数返回的相机矩阵，要么是输入 cameraMatrix 的精确副本（当 centerPrincipalPoint=false 时），要么是修改后的矩阵（当 centerPrincipalPoint=true 时）。

在后一种情况下，新的相机矩阵将是

\[\begin{bmatrix} f_x && 0 && ( \texttt{imgSize.width} -1)*0.5 \\ 0 && f_y && ( \texttt{imgSize.height} -1)*0.5 \\ 0 && 0 && 1 \end{bmatrix} ,\]

其中 \(f_x\) 和 \(f_y\) 分别是 cameraMatrix 的 \((0,0)\) 和 \((1,1)\) 元素。

默认情况下，OpenCV 中的去畸变函数（参见 initUndistortRectifyMap、undistort）不会移动主点。然而，当您使用立体视觉时，将两个视图中的主点移动到相同的 y 坐标（这是大多数立体对应算法所要求的）可能很重要，也可能需要移动到相同的 x 坐标。因此，您可以为每个视图形成新的相机矩阵，其中主点位于中心。

参数

cameraMatrix	输入相机矩阵。
imgsize	相机视图图像的像素大小。
centerPrincipalPoint	新相机矩阵中主点的位置。该参数指示此位置是否应位于图像中心。

getOptimalNewCameraMatrix()

Mat cv::getOptimalNewCameraMatrix	(	InputArray	cameraMatrix,
		InputArray	distCoeffs,
		Size	imageSize,
		double	alpha,
		Size	newImgSize = Size(),
		Rect *	validPixROI = 0,
		bool	centerPrincipalPoint = false )

Python
	cv.getOptimalNewCameraMatrix(	cameraMatrix, distCoeffs, imageSize, alpha[, newImgSize[, centerPrincipalPoint]]	) ->	retval, validPixROI

#include <opencv2/calib3d.hpp>

根据自由缩放参数返回新的相机内参矩阵。

参数

cameraMatrix	输入相机内参矩阵。
distCoeffs	输入畸变系数向量 \(\distcoeffs\)。如果向量为 NULL/空，则假定畸变系数为零。
imageSize	原始图像尺寸。
alpha	自由缩放参数，介于 0（去畸变图像中的所有像素都有效）和 1（原始图像的所有像素都保留在去畸变图像中）之间。详情请参阅 stereoRectify。
newImgSize	校正后的图像尺寸。默认情况下，它设置为 imageSize。
validPixROI	可选输出矩形，用于勾勒出去畸变图像中的所有良好像素区域。请参阅 stereoRectify 中 roi1、roi2 的描述。
centerPrincipalPoint	可选标志，指示新相机内参矩阵中的主点是否应位于图像中心。默认情况下，选择主点以最佳拟合源图像的子集（由 alpha 确定）到校正后的图像。

返回

new_camera_matrix 输出新的相机内参矩阵。

该函数根据自由缩放参数计算并返回最佳新相机内参矩阵。通过改变此参数，您可以只检索有意义的像素（alpha=0），如果角落中有有价值的信息，则保留所有原始图像像素（alpha=1），或者介于两者之间。当 alpha>0 时，去畸变结果可能有一些黑色像素，对应于捕获的畸变图像之外的“虚拟”像素。原始相机内参矩阵、畸变系数、计算出的新相机内参矩阵和 newImageSize 应传递给 initUndistortRectifyMap 以生成 remap 的映射。

getValidDisparityROI()

Rect cv::getValidDisparityROI	(	Rect	roi1,
		Rect	roi2,
		int	minDisparity,
		int	numberOfDisparities,
		int	blockSize )

Python
	cv.getValidDisparityROI(	roi1, roi2, minDisparity, numberOfDisparities, blockSize	) ->	retval

#include <opencv2/calib3d.hpp>

从校正图像的有效ROI（由 stereoRectify 返回）计算有效视差ROI

initCameraMatrix2D()

Mat cv::initCameraMatrix2D	(	InputArrayOfArrays	objectPoints,
		InputArrayOfArrays	imagePoints,
		Size	imageSize,
		double	aspectRatio = 1.0 )

Python
	cv.initCameraMatrix2D(	objectPoints, imagePoints, imageSize[, aspectRatio]	) ->	retval

#include <opencv2/calib3d.hpp>

从三维-二维点对应关系中找到初始相机内参矩阵。

参数

objectPoints	校准模式坐标空间中校准模式点的向量集合。在旧接口中，所有按视图的向量都被连接起来。详情请参阅 calibrateCamera。
imagePoints	校准模式点投影的向量集合。在旧接口中，所有按视图的向量都被连接起来。
imageSize	用于初始化主点的图像像素大小。
aspectRatio	如果为零或负数，则 \(f_x\) 和 \(f_y\) 都将独立估计。否则，\(f_x = f_y \cdot \texttt{aspectRatio}\)。

该函数估计并返回用于相机校准过程的初始相机内参矩阵。目前，该函数仅支持平面校准模式，即每个对象点 z 坐标为 0 的模式。

initInverseRectificationMap()

void cv::initInverseRectificationMap	(	InputArray	cameraMatrix,
		InputArray	distCoeffs,
		InputArray	R,
		InputArray	newCameraMatrix,
		const Size &	size,
		int	m1type,
		OutputArray	map1,
		OutputArray	map2 )

Python
	cv.initInverseRectificationMap(	cameraMatrix, distCoeffs, R, newCameraMatrix, size, m1type[, map1[, map2]]	) ->	map1, map2

#include <opencv2/calib3d.hpp>

计算投影和逆校正变换图。本质上，这是 initUndistortRectifyMap 的逆操作，用于适应投影仪-相机对中投影仪（“逆相机”）的立体校正。

该函数计算联合投影和逆校正变换，并以映射的形式表示结果，供 remap 使用。投影图像看起来是原始图像的扭曲版本，一旦通过投影仪投影，应该在视觉上与原始图像匹配。对于单目相机，newCameraMatrix 通常等于 cameraMatrix，或者可以通过 getOptimalNewCameraMatrix 计算以更好地控制缩放。对于投影仪-相机对，newCameraMatrix 通常设置为由 stereoRectify 计算的 P1 或 P2。

根据 R，投影仪在坐标空间中具有不同的方向。对于投影仪-相机对，这有助于对齐投影仪（与相机使用 initUndistortRectifyMap 的方式相同）以创建立体校正对。这使得两张图像上的对极线变为水平，并具有相同的 y 坐标（对于水平对齐的投影仪-相机对）。

该函数为 remap 使用的逆映射算法构建映射。也就是说，对于目标（投影和逆校正）图像中的每个像素 \((u, v)\)，该函数计算源图像（即原始数字图像）中的相应坐标。应用以下过程：

\[ \begin{array}{l} \text{新相机矩阵}\\ x \leftarrow (u - {c'}_x)/{f'}_x \\ y \leftarrow (v - {c'}_y)/{f'}_y \\ \\\text{去畸变} \\\scriptsize{\textit{尽管所示方程用于径向去畸变，但函数实现了 cv::undistortPoints()}}\\ r^2 \leftarrow x^2 + y^2 \\ \theta \leftarrow \frac{1 + k_1 r^2 + k_2 r^4 + k_3 r^6}{1 + k_4 r^2 + k_5 r^4 + k_6 r^6}\\ x' \leftarrow \frac{x}{\theta} \\ y' \leftarrow \frac{y}{\theta} \\ \\\text{校正}\\ {[X\,Y\,W]} ^T \leftarrow R*[x' \, y' \, 1]^T \\ x'' \leftarrow X/W \\ y'' \leftarrow Y/W \\ \\\text{相机矩阵}\\ map_x(u,v) \leftarrow x''' f_x + c_x \\ map_y(u,v) \leftarrow y''' f_y + c_y \end{array} \]

其中 \((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\) 是畸变系数向量 distCoeffs。

对于立体校正的投影仪-相机对，此函数用于投影仪，而 initUndistortRectifyMap 用于相机。这在调用 stereoRectify 之后完成，而 stereoRectify 又是在调用 stereoCalibrate 之后完成。如果投影仪-相机对未校准，仍然可以使用 stereoRectifyUncalibrated 直接从基础矩阵计算校正变换。对于投影仪和相机，该函数计算单应性 H 作为像素域中的校正变换，而不是 3D 空间中的旋转矩阵 R。R 可以从 H 计算为：

\[\texttt{R} = \texttt{cameraMatrix} ^{-1} \cdot \texttt{H} \cdot \texttt{cameraMatrix}\]

其中 cameraMatrix 可以任意选择。

参数

cameraMatrix	输入相机矩阵 \(A=\vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。
distCoeffs	输入畸变系数向量 \((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含 4、5、8、12 或 14 个元素。如果向量为 NULL/空，则假定畸变系数为零。
R	对象空间中可选的校正变换（3x3矩阵）。此处可以传递由 stereoRectify 计算的 R1 或 R2。如果矩阵为空，则假定为单位变换。
newCameraMatrix	新相机矩阵 \(A'=\vecthreethree{f_x'}{0}{c_x'}{0}{f_y'}{c_y'}{0}{0}{1}\)。
size	畸变图像尺寸。
m1type	第一个输出映射的类型。可以是 CV_32FC1、CV_32FC2 或 CV_16SC2，请参阅 convertMaps
map1	用于 remap 的第一个输出映射。
map2	用于 remap 的第二个输出映射。

initUndistortRectifyMap()

void cv::initUndistortRectifyMap	(	InputArray	cameraMatrix,
		InputArray	distCoeffs,
		InputArray	R,
		InputArray	newCameraMatrix,
		Size	size,
		int	m1type,
		OutputArray	map1,
		OutputArray	map2 )

Python
	cv.initUndistortRectifyMap(	cameraMatrix, distCoeffs, R, newCameraMatrix, size, m1type[, map1[, map2]]	) ->	map1, map2

#include <opencv2/calib3d.hpp>

计算去畸变和校正变换图。

该函数计算联合去畸变和校正变换，并以映射的形式表示结果，供 remap 使用。去畸变后的图像看起来像原始图像，仿佛是用相机以 camera matrix =newCameraMatrix 和零畸变捕获的。对于单目相机，newCameraMatrix 通常等于 cameraMatrix，或者可以通过 getOptimalNewCameraMatrix 计算以更好地控制缩放。对于立体相机，newCameraMatrix 通常设置为由 stereoRectify 计算的 P1 或 P2。

此外，根据 R，这个新相机在坐标空间中具有不同的方向。例如，这有助于对齐立体相机的两个摄像头，使两张图像上的对极线变为水平并具有相同的 y 坐标（对于水平对齐的立体相机）。

该函数实际上为 remap 使用的逆映射算法构建映射。也就是说，对于目标（校正和已校正）图像中的每个像素 \((u, v)\)，该函数计算源图像（即相机原始图像）中的相应坐标。应用以下过程：

\[ \begin{array}{l} x \leftarrow (u - {c'}_x)/{f'}_x \\ y \leftarrow (v - {c'}_y)/{f'}_y \\ {[X\,Y\,W]} ^T \leftarrow R^{-1}*[x \, y \, 1]^T \\ x' \leftarrow X/W \\ y' \leftarrow Y/W \\ r^2 \leftarrow x'^2 + y'^2 \\ x'' \leftarrow x' \frac{1 + k_1 r^2 + k_2 r^4 + k_3 r^6}{1 + k_4 r^2 + k_5 r^4 + k_6 r^6} + 2p_1 x' y' + p_2(r^2 + 2 x'^2) + s_1 r^2 + s_2 r^4\\ y'' \leftarrow y' \frac{1 + k_1 r^2 + k_2 r^4 + k_3 r^6}{1 + k_4 r^2 + k_5 r^4 + k_6 r^6} + p_1 (r^2 + 2 y'^2) + 2 p_2 x' y' + s_3 r^2 + s_4 r^4 \\ s\vecthree{x'''}{y'''}{1} = \vecthreethree{R_{33}(\tau_x, \tau_y)}{0}{-R_{13}((\tau_x, \tau_y)} {0}{R_{33}(\tau_x, \tau_y)}{-R_{23}(\tau_x, \tau_y)} {0}{0}{1} R(\tau_x, \tau_y) \vecthree{x''}{y''}{1}\\ map_x(u,v) \leftarrow x''' f_x + c_x \\ map_y(u,v) \leftarrow y''' f_y + c_y \end{array} \]

其中 \((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\) 是畸变系数。

对于立体相机，此函数会被调用两次：在 stereoRectify 之后，每个相机头调用一次；而 stereoRectify 又是在 stereoCalibrate 之后被调用。但是，如果立体相机未校准，仍然可以使用 stereoRectifyUncalibrated 直接从基础矩阵计算校正变换。对于每个相机，该函数计算单应性 H 作为像素域中的校正变换，而不是 3D 空间中的旋转矩阵 R。R 可以从 H 计算为：

\[\texttt{R} = \texttt{cameraMatrix} ^{-1} \cdot \texttt{H} \cdot \texttt{cameraMatrix}\]

其中 cameraMatrix 可以任意选择。

参数

cameraMatrix	输入相机矩阵 \(A=\vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。
distCoeffs	输入畸变系数向量 \((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含 4、5、8、12 或 14 个元素。如果向量为 NULL/空，则假定畸变系数为零。
R	对象空间中可选的校正变换（3x3矩阵）。此处可以传递由 stereoRectify 计算的 R1 或 R2。如果矩阵为空，则假定为单位变换。在 initUndistortRectifyMap 中，R 假定为单位矩阵。
newCameraMatrix	新相机矩阵 \(A'=\vecthreethree{f_x'}{0}{c_x'}{0}{f_y'}{c_y'}{0}{0}{1}\)。
size	去畸变图像尺寸。
m1type	第一个输出映射的类型，可以是 CV_32FC1、CV_32FC2 或 CV_16SC2，请参阅 convertMaps
map1	第一个输出映射。
map2	第二个输出映射。

initWideAngleProjMap() [1/2]

float cv::initWideAngleProjMap	(	InputArray	cameraMatrix,
		InputArray	distCoeffs,
		Size	imageSize,
		int	destImageWidth,
		int	m1type,
		OutputArray	map1,
		OutputArray	map2,
		enum UndistortTypes	projType = PROJ_SPHERICAL_EQRECT,
		double	alpha = 0 )

#include <opencv2/calib3d.hpp>

为广角相机初始化 remap 的映射

initWideAngleProjMap() [2/2]

static float cv::initWideAngleProjMap ( InputArray cameraMatrix, InputArray distCoeffs, Size imageSize, int destImageWidth, int m1type, OutputArray map1, OutputArray map2, int projType, double alpha = 0 )

inlinestatic

#include <opencv2/calib3d.hpp>

此函数的调用图如下

matMulDeriv()

void cv::matMulDeriv	(	InputArray	A,
		InputArray	B,
		OutputArray	dABdA,
		OutputArray	dABdB )

Python
	cv.matMulDeriv(	A, B[, dABdA[, dABdB]]	) ->	dABdA, dABdB

#include <opencv2/calib3d.hpp>

计算每个相乘矩阵的矩阵乘积偏导数。

参数

A	第一个相乘的矩阵。
B	第二个相乘的矩阵。
dABdA	第一个输出导数矩阵 d(A*B)/dA，大小为 \(\texttt{A.rows*B.cols} \times {A.rows*A.cols}\)。
dABdB	第二个输出导数矩阵 d(A*B)/dB，大小为 \(\texttt{A.rows*B.cols} \times {B.rows*B.cols}\)。

该函数计算矩阵乘积 \(A*B\) 元素相对于两个输入矩阵各自元素的偏导数。该函数用于在 stereoCalibrate 中计算雅可比矩阵，但也可以用于任何其他类似的优化函数。

projectPoints()

void cv::projectPoints	(	InputArray	objectPoints,
		InputArray	rvec,
		InputArray	tvec,
		InputArray	cameraMatrix,
		InputArray	distCoeffs,
		OutputArray	imagePoints,
		OutputArray	jacobian = noArray(),
		double	aspectRatio = 0 )

Python
	cv.projectPoints(	objectPoints, rvec, tvec, cameraMatrix, distCoeffs[, imagePoints[, jacobian[, aspectRatio]]]	) ->	imagePoints, jacobian

#include <opencv2/calib3d.hpp>

将三维点投影到图像平面。

参数

objectPoints	相对于世界坐标系表示的对象点数组。一个 3xN/Nx3 1通道或 1xN/Nx1 3通道（或 vector<Point3f> ）矩阵，其中 N 是视图中的点数。
rvec	旋转向量（Rodrigues），与 tvec 一起，执行从世界坐标系到相机坐标系的基变换，详情请参阅 calibrateCamera。
tvec	平移向量，请参阅上面的参数描述。
cameraMatrix	相机内参矩阵 \(\cameramatrix{A}\)。
distCoeffs	输入畸变系数向量 \(\distcoeffs\)。如果向量为空，则假定畸变系数为零。
imagePoints	图像点的输出数组，1xN/Nx1 2通道，或 vector<Point2f>。
jacobian	可选的输出 2Nx(10+<numDistCoeffs>) 雅可比矩阵，包含图像点相对于旋转向量、平移向量、焦距、主点坐标和畸变系数分量的导数。在旧接口中，雅可比矩阵的不同分量通过不同的输出参数返回。
aspectRatio	可选的“固定纵横比”参数。如果该参数不为 0，则函数假定纵横比 ( \(f_x / f_y\)) 是固定的，并相应地调整雅可比矩阵。

该函数根据内参和外参计算 3D 点在图像平面上的 2D 投影。可选地，该函数计算雅可比矩阵——图像点坐标（作为所有输入参数的函数）相对于特定参数（内参和/或外参）的偏导数矩阵。雅可比矩阵用于 calibrateCamera、solvePnP 和 stereoCalibrate 中的全局优化。该函数本身也可以用于计算重投影误差，给定当前的内参和外参。

注意

通过设置 rvec = tvec = \([0, 0, 0]\)，或将 cameraMatrix 设置为 3x3 单位矩阵，或传入零畸变系数，可以得到该函数的各种有用特例。这意味着，可以在理想的零畸变设置中计算稀疏点集的畸变坐标或应用透视变换（并计算导数）。

recoverPose() [1/4]

int cv::recoverPose	(	InputArray	输入的本质矩阵。,
		InputArray	3x3基本矩阵。,
		InputArray	包含第一组点的1xN数组。,
		InputArray	cameraMatrix,
		OutputArray	R,
		OutputArray	t,
		double	distanceThresh,
		InputOutputArray	mask = noArray(),
		OutputArray	triangulatedPoints = noArray() )

Python
	cv.recoverPose(	points1, points2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2[, E[, R[, t[, method[, prob[, threshold[, mask]]]]]]]	) ->	retval, E, R, t, mask
	cv.recoverPose(	E, points1, points2, cameraMatrix[, R[, t[, mask]]]	) ->	retval, R, t, mask
	cv.recoverPose(	E, points1, points2[, R[, t[, focal[, pp[, mask]]]]]	) ->	retval, R, t, mask
	cv.recoverPose(	E, points1, points2, cameraMatrix, distanceThresh[, R[, t[, mask[, triangulatedPoints]]]]	) ->	retval, R, t, mask, triangulatedPoints

#include <opencv2/calib3d.hpp>

这是一个重载的成员函数，为方便起见而提供。它与上述函数的区别仅在于它接受的参数。

参数

输入的本质矩阵。	输入的本质矩阵。
3x3基本矩阵。	来自第一张图像的 N 个 2D 点数组。点坐标应为浮点数（单精度或双精度）。
包含第一组点的1xN数组。	第二张图像的点数组，与points1尺寸和格式相同。
cameraMatrix	相机内参矩阵 \(\cameramatrix{A}\)。请注意，此函数假定 points1 和 points2 是来自具有相同相机内参矩阵的相机的特征点。
R	输出旋转矩阵。此矩阵与平移向量一起构成一个元组，执行从第一个相机坐标系到第二个相机坐标系的基变换。请注意，通常情况下，t 不能用于此元组，请参阅下面的参数描述。
t	输出平移向量。此向量由 decomposeEssentialMat 获得，因此只知道其尺度，即 t 是平移向量的方向，且具有单位长度。
distanceThresh	阈值距离，用于过滤掉远距离点（即无限远点）。
mask	points1 和 points2 中内点的输入/输出掩码。如果它不为空，则它会标记给定基本矩阵 E 的 points1 和 points2 中的内点。只有这些内点将用于恢复姿态。在输出掩码中，只有通过手性检查的内点。
triangulatedPoints	通过三角测量重建的 3D 点。

此函数与上述函数不同之处在于，它输出用于手性检查的三角化 3D 点。

recoverPose() [2/4]

int cv::recoverPose	(	InputArray	输入的本质矩阵。,
		InputArray	3x3基本矩阵。,
		InputArray	包含第一组点的1xN数组。,
		InputArray	cameraMatrix,
		OutputArray	R,
		OutputArray	t,
		InputOutputArray	mask = noArray() )

Python
	cv.recoverPose(	points1, points2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2[, E[, R[, t[, method[, prob[, threshold[, mask]]]]]]]	) ->	retval, E, R, t, mask
	cv.recoverPose(	E, points1, points2, cameraMatrix[, R[, t[, mask]]]	) ->	retval, R, t, mask
	cv.recoverPose(	E, points1, points2[, R[, t[, focal[, pp[, mask]]]]]	) ->	retval, R, t, mask
	cv.recoverPose(	E, points1, points2, cameraMatrix, distanceThresh[, R[, t[, mask[, triangulatedPoints]]]]	) ->	retval, R, t, mask, triangulatedPoints

#include <opencv2/calib3d.hpp>

从估计的本征矩阵和两张图像中的对应点恢复相对相机旋转和平移，并进行手性检查。返回通过检查的内点数。

参数

输入的本质矩阵。	输入的本质矩阵。
3x3基本矩阵。	来自第一张图像的 N 个 2D 点数组。点坐标应为浮点数（单精度或双精度）。
包含第一组点的1xN数组。	第二张图像的点数组，与points1尺寸和格式相同。
cameraMatrix	相机内参矩阵 \(\cameramatrix{A}\)。请注意，此函数假定 points1 和 points2 是来自具有相同相机内参矩阵的相机的特征点。
R	输出旋转矩阵。此矩阵与平移向量一起构成一个元组，执行从第一个相机坐标系到第二个相机坐标系的基变换。请注意，通常情况下，t 不能用于此元组，请参阅下面描述的参数。
t	输出平移向量。此向量由 decomposeEssentialMat 获得，因此只知道其尺度，即 t 是平移向量的方向，且具有单位长度。
mask	points1 和 points2 中内点的输入/输出掩码。如果它不为空，则它会标记给定基本矩阵 E 的 points1 和 points2 中的内点。只有这些内点将用于恢复姿态。在输出掩码中，只有通过手性检查的内点。

此函数使用 decomposeEssentialMat 分解基本矩阵，然后通过手性检查验证可能的姿态假设。手性检查意味着三角化 3D 点应具有正深度。更多详细信息请参见 [211]。

此函数可用于处理来自 findEssentialMat 的输出 E 和掩码。在此场景中，points1 和 points2 是 findEssentialMat 的相同输入。

// 示例：使用RANSAC算法估计基础矩阵
int point_count = 100;
vector<Point2f> points1(point_count);
vector<Point2f> points2(point_count);
 
// 在这里初始化点...
for( int i = 0; i < point_count; i++ )
{
points1[i] = ...;
points2[i] = ...;
}
 
// 相机矩阵，两个焦距都为1，主点为(0, 0)
Mat cameraMatrix = Mat::eye(3, 3, CV_64F);
 
Mat E, R, t, mask;
 
E = findEssentialMat(points1, points2, cameraMatrix, RANSAC, 0.999, 1.0, mask);
recoverPose(E, points1, points2, cameraMatrix, R, t, mask);

recoverPose() [3/4]

int cv::recoverPose	(	InputArray	输入的本质矩阵。,
		InputArray	3x3基本矩阵。,
		InputArray	包含第一组点的1xN数组。,
		OutputArray	R,
		OutputArray	t,
		double	focal = 1.0,
		Point2d	pp = Point2d(0, 0),
		InputOutputArray	mask = noArray() )

Python
	cv.recoverPose(	points1, points2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2[, E[, R[, t[, method[, prob[, threshold[, mask]]]]]]]	) ->	retval, E, R, t, mask
	cv.recoverPose(	E, points1, points2, cameraMatrix[, R[, t[, mask]]]	) ->	retval, R, t, mask
	cv.recoverPose(	E, points1, points2[, R[, t[, focal[, pp[, mask]]]]]	) ->	retval, R, t, mask
	cv.recoverPose(	E, points1, points2, cameraMatrix, distanceThresh[, R[, t[, mask[, triangulatedPoints]]]]	) ->	retval, R, t, mask, triangulatedPoints

#include <opencv2/calib3d.hpp>

这是一个重载的成员函数，为方便起见而提供。它与上述函数的区别仅在于它接受的参数。

参数

输入的本质矩阵。	输入的本质矩阵。
3x3基本矩阵。	来自第一张图像的 N 个 2D 点数组。点坐标应为浮点数（单精度或双精度）。
包含第一组点的1xN数组。	第二张图像的点数组，与points1尺寸和格式相同。
R	输出旋转矩阵。此矩阵与平移向量一起构成一个元组，执行从第一个相机坐标系到第二个相机坐标系的基变换。请注意，通常情况下，t 不能用于此元组，请参阅下面的参数描述。
t	输出平移向量。此向量由 decomposeEssentialMat 获得，因此只知道其尺度，即 t 是平移向量的方向，且具有单位长度。
相机焦距。请注意，此函数假设points1和points2是来自具有相同焦距和主点的相机的特征点。	相机的焦距。请注意，此函数假定 points1 和 points2 是来自具有相同焦距和主点的相机的特征点。
相机主点。	相机主点。
mask	points1 和 points2 中内点的输入/输出掩码。如果它不为空，则它会标记给定基本矩阵 E 的 points1 和 points2 中的内点。只有这些内点将用于恢复姿态。在输出掩码中，只有通过手性检查的内点。

此函数与上一个函数的不同之处在于，它从焦距和主点计算相机内参矩阵

\[A = \begin{bmatrix} f & 0 & x_{pp} \\ 0 & f & y_{pp} \\ 0 & 0 & 1 \end{bmatrix}\]

recoverPose() [4/4]

int cv::recoverPose	(	InputArray	3x3基本矩阵。,
		InputArray	包含第一组点的1xN数组。,
		InputArray	第一个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。,
		InputArray	第一个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。,
		InputArray	第二个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。,
		InputArray	第二个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。,
		OutputArray	输入的本质矩阵。,
		OutputArray	R,
		OutputArray	t,
		int	method = cv::RANSAC,
		double	prob = 0.999,
		double	threshold = 1.0,
		InputOutputArray	mask = noArray() )

Python
	cv.recoverPose(	points1, points2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2[, E[, R[, t[, method[, prob[, threshold[, mask]]]]]]]	) ->	retval, E, R, t, mask
	cv.recoverPose(	E, points1, points2, cameraMatrix[, R[, t[, mask]]]	) ->	retval, R, t, mask
	cv.recoverPose(	E, points1, points2[, R[, t[, focal[, pp[, mask]]]]]	) ->	retval, R, t, mask
	cv.recoverPose(	E, points1, points2, cameraMatrix, distanceThresh[, R[, t[, mask[, triangulatedPoints]]]]	) ->	retval, R, t, mask, triangulatedPoints

#include <opencv2/calib3d.hpp>

从两台不同摄像机的两张图像中对应的点恢复相对摄像机旋转和平移，并使用手性检查。返回通过检查的内点数量。

参数

3x3基本矩阵。	来自第一张图像的 N 个 2D 点数组。点坐标应为浮点数（单精度或双精度）。
包含第一组点的1xN数组。	第二张图像的点数组，与points1尺寸和格式相同。
第一个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。	第一个相机的输入/输出相机矩阵，与 calibrateCamera 中的相同。此外，对于立体情况，可以使用附加标志，请参见下文。
第一个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。	畸变系数的输入/输出向量，与 calibrateCamera 中的相同。
第二个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。	第一个相机的输入/输出相机矩阵，与 calibrateCamera 中的相同。此外，对于立体情况，可以使用附加标志，请参见下文。
第二个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。	畸变系数的输入/输出向量，与 calibrateCamera 中的相同。
输入的本质矩阵。	输出基本矩阵。
R	输出旋转矩阵。此矩阵与平移向量一起构成一个元组，执行从第一个相机坐标系到第二个相机坐标系的基变换。请注意，通常情况下，t 不能用于此元组，请参阅下面描述的参数。
t	输出平移向量。此向量由 decomposeEssentialMat 获得，因此只知道其尺度，即 t 是平移向量的方向，且具有单位长度。
方法	计算本质矩阵的方法。 RANSAC 用于RANSAC算法。 LMEDS 用于LMedS算法。
仅用于RANSAC或LMedS方法的参数。它指定了估计矩阵正确的期望置信水平（概率）。	仅用于RANSAC或LMedS方法的参数。它指定了估计矩阵正确的期望置信水平（概率）。
RANSAC参数。它是点到像素中对极线的最大距离，超过此距离的点将被视为异常值，不用于计算最终的基本矩阵。它可以设置为1-3左右，具体取决于点定位的精度、图像分辨率和图像噪声。	RANSAC参数。它是点到像素中对极线的最大距离，超过此距离的点将被视为异常值，不用于计算最终的基本矩阵。它可以设置为1-3左右，具体取决于点定位的精度、图像分辨率和图像噪声。
mask	points1 和 points2 中内点的输入/输出掩码。如果它不为空，则它会标记给定基本矩阵 E 的 points1 和 points2 中的内点。只有这些内点将用于恢复姿态。在输出掩码中，只有通过手性检查的内点。

此函数使用 decomposeEssentialMat 分解基本矩阵，然后通过手性检查验证可能的姿态假设。手性检查意味着三角化 3D 点应具有正深度。更多详细信息请参见 [211]。

此函数可用于处理来自 findEssentialMat 的输出 E 和掩码。在此场景中，points1 和 points2 是 findEssentialMat 的相同输入。

// 示例：使用RANSAC算法估计基础矩阵
int point_count = 100;
vector<Point2f> points1(point_count);
vector<Point2f> points2(point_count);
 
// 在这里初始化点...
for( int i = 0; i < point_count; i++ )
{
points1[i] = ...;
points2[i] = ...;
}
 
// 输入：两个相机的相机校准，例如使用棋盘格内参校准。
Mat cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2;
 
// 输出：基本矩阵、相对旋转和相对平移。
Mat E, R, t, mask;
 
recoverPose(points1, points2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, E, R, t, mask);

rectify3Collinear()

float cv::rectify3Collinear	(	InputArray	第一个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。,
		InputArray	第一个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。,
		InputArray	第二个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。,
		InputArray	第二个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。,
		InputArray	cameraMatrix3,
		InputArray	distCoeffs3,
		InputArrayOfArrays	imgpt1,
		InputArrayOfArrays	imgpt3,
		Size	imageSize,
		InputArray	R12,
		InputArray	T12,
		InputArray	R13,
		InputArray	T13,
		OutputArray	一个可能的旋转矩阵。,
		OutputArray	另一个可能的旋转矩阵。,
		OutputArray	R3,
		OutputArray	P1,
		OutputArray	P2,
		OutputArray	P3,
		OutputArray	Q,
		double	alpha,
		Size	newImgSize,
		Rect *	roi1,
		Rect *	roi2,
		int	flags )

Python
	cv.rectify3Collinear(	cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, cameraMatrix3, distCoeffs3, imgpt1, imgpt3, imageSize, R12, T12, R13, T13, alpha, newImgSize, flags[, R1[, R2[, R3[, P1[, P2[, P3[, Q]]]]]]]	) ->	retval, R1, R2, R3, P1, P2, P3, Q, roi1, roi2

#include <opencv2/calib3d.hpp>

计算3头摄像机的校正变换，其中所有摄像头位于同一直线上。

reprojectImageTo3D()

void cv::reprojectImageTo3D	(	InputArray	disparity,
		OutputArray	_3dImage,
		InputArray	Q,
		bool	handleMissingValues = false,
		int	ddepth = -1 )

Python
	cv.reprojectImageTo3D(	disparity, Q[, _3dImage[, handleMissingValues[, ddepth]]]	) ->	_3dImage

#include <opencv2/calib3d.hpp>

将视差图像重新投影到3D空间。

参数

disparity	输入单通道 8 位无符号、16 位有符号、32 位有符号或 32 位浮点视差图像。8 位/16 位有符号格式的值假定没有小数位。如果视差是 16 位有符号格式，如由 StereoBM 或 StereoSGBM 以及可能其他算法计算的，则在使用前应将其除以 16（并缩放到浮点数）。
_3dImage	输出 3 通道浮点图像，与视差图像大小相同。_3dImage(x,y) 的每个元素都包含从视差图计算的点 (x,y) 的 3D 坐标。如果使用通过 stereoRectify 获得的 Q，则返回的点表示在第一个相机的校正坐标系中。
Q	可以通过 stereoRectify 获得的 \(4 \times 4\) 透视变换矩阵。
handleMissingValues	指示函数是否应处理缺失值（即未计算视差的点）。如果 handleMissingValues=true，则将与异常值对应的最小视差像素（参见 StereoMatcher::compute）转换为具有非常大 Z 值（当前设置为 10000）的 3D 点。
ddepth	可选的输出数组深度。如果为 -1，则输出图像将具有 CV_32F 深度。ddepth 也可以设置为 CV_16S、CV_32S 或 CV_32F。

该函数将单通道视差图转换为表示 3D 表面的 3 通道图像。也就是说，对于每个像素 (x,y) 和相应的视差 d=disparity(x,y)，它计算：

\[\begin{bmatrix} X \\ Y \\ Z \\ W \end{bmatrix} = Q \begin{bmatrix} x \\ y \\ \texttt{disparity} (x,y) \\ 1 \end{bmatrix}.\]

另请参见

要将稀疏点集 {(x,y,d),...} 重投影到 3D 空间，请使用 perspectiveTransform。

Rodrigues()

void cv::Rodrigues	(	InputArray	src,
		OutputArray	dst,
		OutputArray	jacobian = noArray() )

Python
	cv.Rodrigues(	src[, dst[, jacobian]]	) ->	dst, jacobian

#include <opencv2/calib3d.hpp>

将旋转矩阵转换为旋转向量，反之亦然。

参数

src	输入旋转向量（3x1 或 1x3）或旋转矩阵（3x3）。
dst	输出旋转矩阵（3x3）或旋转向量（3x1 或 1x3），分别对应。
jacobian	可选的输出雅可比矩阵，3x9 或 9x3，是输出数组分量相对于输入数组分量的偏导数矩阵。

\[\begin{array}{l} \theta \leftarrow norm(r) \\ r \leftarrow r/ \theta \\ R = \cos(\theta) I + (1- \cos{\theta} ) r r^T + \sin(\theta) \vecthreethree{0}{-r_z}{r_y}{r_z}{0}{-r_x}{-r_y}{r_x}{0} \end{array}\]

逆变换也可以轻松完成，因为

\[\sin ( \theta ) \vecthreethree{0}{-r_z}{r_y}{r_z}{0}{-r_x}{-r_y}{r_x}{0} = \frac{R - R^T}{2}\]

旋转向量是旋转矩阵的一种方便且最紧凑的表示（因为任何旋转矩阵只有 3 个自由度）。这种表示用于全局 3D 几何优化过程，如 calibrateCamera、stereoCalibrate 或 solvePnP。

注意

关于 3D 旋转矩阵相对于其指数坐标的导数计算的更多信息可在以下参考文献中找到：

• A Compact Formula for the Derivative of a 3-D Rotation in Exponential Coordinates, Guillermo Gallego, Anthony J. Yezzi [98]

关于 SE(3) 和李群的有用信息可在以下参考文献中找到：

• A tutorial on SE(3) transformation parameterizations and on-manifold optimization, Jose-Luis Blanco [30]
• Lie Groups for 2D and 3D Transformation, Ethan Eade [80]
• A micro Lie theory for state estimation in robotics, Joan Solà, Jérémie Deray, Dinesh Atchuthan [252]

RQDecomp3x3()

Vec3d cv::RQDecomp3x3	(	InputArray	src,
		OutputArray	mtxR,
		OutputArray	mtxQ,
		OutputArray	Qx = noArray(),
		OutputArray	Qy = noArray(),
		OutputArray	Qz = noArray() )

Python
	cv.RQDecomp3x3(	src[, mtxR[, mtxQ[, Qx[, Qy[, Qz]]]]]	) ->	retval, mtxR, mtxQ, Qx, Qy, Qz

#include <opencv2/calib3d.hpp>

计算3x3矩阵的RQ分解。

参数

src	3x3 输入矩阵。
mtxR	输出 3x3 上三角矩阵。
mtxQ	输出 3x3 正交矩阵。
Qx	可选输出 3x3 绕 x 轴旋转矩阵。
Qy	可选输出 3x3 绕 y 轴旋转矩阵。
Qz	可选输出 3x3 绕 z 轴旋转矩阵。

该函数使用给定的旋转计算RQ分解。此函数用于decomposeProjectionMatrix，将投影矩阵的左上角3x3子矩阵分解为相机矩阵和旋转矩阵。

它可选地返回三个旋转矩阵，每个轴一个，以及可在OpenGL中使用的以度为单位的三个欧拉角（作为返回值）。请注意，始终存在不止一种围绕三个主轴的旋转序列，可以使对象达到相同的方向，例如参见[251]。返回的三个旋转矩阵和相应的三个欧拉角只是可能的解决方案之一。

sampsonDistance()

double cv::sampsonDistance	(	InputArray	pt1,
		InputArray	pt2,
		InputArray	F )

Python
	cv.sampsonDistance(	pt1, pt2, F	) ->	retval

#include <opencv2/calib3d.hpp>

计算两点之间的Sampson距离。

函数cv::sampsonDistance计算并返回几何误差的一阶近似值，如下所示：

\[ sd( \texttt{pt1} , \texttt{pt2} )= \frac{(\texttt{pt2}^t \cdot \texttt{F} \cdot \texttt{pt1})^2} {((\texttt{F} \cdot \texttt{pt1})(0))^2 + ((\texttt{F} \cdot \texttt{pt1})(1))^2 + ((\texttt{F}^t \cdot \texttt{pt2})(0))^2 + ((\texttt{F}^t \cdot \texttt{pt2})(1))^2} \]

基本矩阵可以使用findFundamentalMat函数计算。详情请参阅[119] 11.4.3。

参数

pt1	第一个齐次2D点
pt2	第二个齐次2D点
基本矩阵，可以使用findFundamentalMat或stereoRectify进行估计。	基本矩阵

返回

计算出的Sampson距离。

solveP3P()

int cv::solveP3P	(	InputArray	objectPoints,
		InputArray	imagePoints,
		InputArray	cameraMatrix,
		InputArray	distCoeffs,
		OutputArrayOfArrays	rvecs,
		OutputArrayOfArrays	tvecs,
		int	flags )

Python
	cv.solveP3P(	objectPoints, imagePoints, cameraMatrix, distCoeffs, flags[, rvecs[, tvecs]]	) ->	retval, rvecs, tvecs

#include <opencv2/calib3d.hpp>

从3个3D-2D点对应关系中查找物体姿态 \( {}^{c}\mathbf{T}_o \) 。

透视投影，从物体坐标系到相机坐标系

另请参见

Perspective-n-Point (PnP) 姿态计算

参数

objectPoints	对象坐标空间中的对象点数组，3x3 1通道或1x3/3x1 3通道。此处也可传递 vector<Point3f>。
imagePoints	对应图像点的数组，3x2 1通道或1x3/3x1 2通道。此处也可传递 vector<Point2f>。
cameraMatrix	输入相机内参矩阵 \(\cameramatrix{A}\) 。
distCoeffs	输入畸变系数向量 \(\distcoeffs\)。如果向量为 NULL/空，则假定畸变系数为零。
rvecs	输出旋转向量（参见Rodrigues），与tvec一起将点从模型坐标系转换到相机坐标系。P3P问题最多有4个解决方案。
tvecs	输出平移向量。
flags	解决P3P问题的方法 SOLVEPNP_P3P 方法基于 X.S. Gao, X.-R. Hou, J. Tang, H.-F. Chang 的论文“Complete Solution Classification for the Perspective-Three-Point Problem” ([99])。 SOLVEPNP_AP3P 方法基于 T. Ke 和 S. Roumeliotis 的论文。“An Efficient Algebraic Solution to the Perspective-Three-Point Problem” ([147])。

该函数根据3个物体点、它们对应的图像投影以及相机内参矩阵和畸变系数来估计物体姿态。

注意

解决方案按重投影误差排序（从低到高）。

solvePnP()

bool cv::solvePnP	(	InputArray	objectPoints,
		InputArray	imagePoints,
		InputArray	cameraMatrix,
		InputArray	distCoeffs,
		OutputArray	rvec,
		OutputArray	tvec,
		bool	useExtrinsicGuess = false,
		int	flags = SOLVEPNP_ITERATIVE )

Python
	cv.solvePnP(	objectPoints, imagePoints, cameraMatrix, distCoeffs[, rvec[, tvec[, useExtrinsicGuess[, flags]]]]	) ->	retval, rvec, tvec

#include <opencv2/calib3d.hpp>

从3D-2D点对应关系中查找物体姿态 \( {}^{c}\mathbf{T}_o \)

透视投影，从物体坐标系到相机坐标系

另请参见

Perspective-n-Point (PnP) 姿态计算

此函数使用不同的方法返回将以物体坐标系表示的3D点转换为相机坐标系的旋转和平移向量

• P3P 方法（SOLVEPNP_P3P, SOLVEPNP_AP3P）：需要4个输入点以返回唯一解。
• SOLVEPNP_IPPE 输入点必须 >= 4 且物体点必须共面。
• SOLVEPNP_IPPE_SQUARE 适用于标记姿态估计的特殊情况。输入点数量必须为4。物体点必须按以下顺序定义
  • 点 0: [-squareLength / 2, squareLength / 2, 0]
  • 点 1: [ squareLength / 2, squareLength / 2, 0]
  • 点 2: [ squareLength / 2, -squareLength / 2, 0]
  • 点 3: [-squareLength / 2, -squareLength / 2, 0]
• 对于所有其他标志，输入点数量必须 >= 4，且物体点可以是任意配置。

参数

objectPoints	物体坐标空间中的物体点数组，Nx3 1通道或1xN/Nx1 3通道，其中N为点数。此处也可传递 vector<Point3d>。
imagePoints	对应图像点的数组，Nx2 1通道或1xN/Nx1 2通道，其中N为点数。此处也可传递 vector<Point2d>。
cameraMatrix	输入相机内参矩阵 \(\cameramatrix{A}\) 。
distCoeffs	输入畸变系数向量 \(\distcoeffs\)。如果向量为 NULL/空，则假定畸变系数为零。
rvec	输出旋转向量（参见Rodrigues），与tvec一起将点从模型坐标系转换到相机坐标系。
tvec	输出平移向量。
useExtrinsicGuess	用于SOLVEPNP_ITERATIVE的参数。如果为true (1)，函数将使用提供的rvec和tvec值分别作为旋转和平移向量的初始近似值，并进一步优化它们。
flags	解决PnP问题的方法：请参阅calib3d_solvePnP_flags

关于Perspective-n-Points的更多信息请参见Perspective-n-Point (PnP) 姿态计算

注意

• 如何在平面增强现实中使用solvePnP的示例可以在opencv_source_code/samples/python/plane_ar.py中找到
• 如果你正在使用Python
  • Numpy数组切片不能作为输入，因为solvePnP需要连续数组（由 modules/calib3d/src/solvepnp.cpp 版本2.4.9 第55行左右使用cv::Mat::checkVector() 的断言强制执行）。
  • P3P 算法要求图像点位于形状为 (N,1,2) 的数组中，因为它调用了undistortPoints（modules/calib3d/src/solvepnp.cpp 版本 2.4.9 大约第 75 行），而该函数需要 2 通道信息。
  • 因此，给定一些数据 D = np.array(...)，其中 D.shape = (N,M)，为了将其子集用作例如 imagePoints，必须有效地将其复制到一个新数组中：imagePoints = np.ascontiguousarray(D[:,:2]).reshape((N,1,2))
• 方法SOLVEPNP_DLS和SOLVEPNP_UPNP不能使用，因为当前的实现不稳定，有时会给出完全错误的结果。如果您传递了这两个标志中的任何一个，则将改为使用SOLVEPNP_EPNP方法。
• 在一般情况下，最小点数为4。对于SOLVEPNP_P3P和SOLVEPNP_AP3P方法，需要精确使用4个点（前3个点用于估计P3P问题的所有解决方案，最后一个点用于保留最小化重投影误差的最佳解决方案）。
• 使用SOLVEPNP_ITERATIVE方法和useExtrinsicGuess=true时，最小点数为3（3个点足以计算姿态，但最多有4个解）。初始解应接近全局解才能收敛。
• 使用SOLVEPNP_IPPE时，输入点必须 >= 4 且物体点必须共面。
• 使用SOLVEPNP_IPPE_SQUARE时，这是适用于标记姿态估计的特殊情况。输入点数量必须为4。物体点必须按以下顺序定义
  • 点 0: [-squareLength / 2, squareLength / 2, 0]
  • 点 1: [ squareLength / 2, squareLength / 2, 0]
  • 点 2: [ squareLength / 2, -squareLength / 2, 0]
  • 点 3: [-squareLength / 2, -squareLength / 2, 0]
• 使用SOLVEPNP_SQPNP时，输入点必须 >= 3

solvePnPGeneric()

int cv::solvePnPGeneric	(	InputArray	objectPoints,
		InputArray	imagePoints,
		InputArray	cameraMatrix,
		InputArray	distCoeffs,
		OutputArrayOfArrays	rvecs,
		OutputArrayOfArrays	tvecs,
		bool	useExtrinsicGuess = false,
		SolvePnPMethod	flags = SOLVEPNP_ITERATIVE,
		InputArray	rvec = noArray(),
		InputArray	tvec = noArray(),
		OutputArray	reprojectionError = noArray() )

Python
	cv.solvePnPGeneric(	objectPoints, imagePoints, cameraMatrix, distCoeffs[, rvecs[, tvecs[, useExtrinsicGuess[, flags[, rvec[, tvec[, reprojectionError]]]]]]]	) ->	retval, rvecs, tvecs, reprojectionError

#include <opencv2/calib3d.hpp>

从3D-2D点对应关系中查找物体姿态 \( {}^{c}\mathbf{T}_o \) 。

透视投影，从物体坐标系到相机坐标系

另请参见

Perspective-n-Point (PnP) 姿态计算

此函数根据输入点的数量和所选方法返回所有可能的解（一个解是<旋转向量，平移向量>对）的列表

• P3P 方法（SOLVEPNP_P3P, SOLVEPNP_AP3P）：3个或4个输入点。使用3个输入点时，返回解的数量可在0到4之间。
• SOLVEPNP_IPPE 输入点必须 >= 4 且物体点必须共面。返回2个解。
• SOLVEPNP_IPPE_SQUARE 适用于标记姿态估计的特殊情况。输入点数量必须为4，并返回2个解。物体点必须按以下顺序定义
  • 点 0: [-squareLength / 2, squareLength / 2, 0]
  • 点 1: [ squareLength / 2, squareLength / 2, 0]
  • 点 2: [ squareLength / 2, -squareLength / 2, 0]
  • 点 3: [-squareLength / 2, -squareLength / 2, 0]
• 对于所有其他标志，输入点数量必须 >= 4 且物体点可以是任意配置。只返回1个解。

参数

objectPoints	物体坐标空间中的物体点数组，Nx3 1通道或1xN/Nx1 3通道，其中N为点数。此处也可传递 vector<Point3d>。
imagePoints	对应图像点的数组，Nx2 1通道或1xN/Nx1 2通道，其中N为点数。此处也可传递 vector<Point2d>。
cameraMatrix	输入相机内参矩阵 \(\cameramatrix{A}\) 。
distCoeffs	输入畸变系数向量 \(\distcoeffs\)。如果向量为 NULL/空，则假定畸变系数为零。
rvecs	输出旋转向量的向量（参见Rodrigues），与tvecs一起将点从模型坐标系转换到相机坐标系。
tvecs	输出平移向量的向量。
useExtrinsicGuess	用于SOLVEPNP_ITERATIVE的参数。如果为true (1)，函数将使用提供的rvec和tvec值分别作为旋转和平移向量的初始近似值，并进一步优化它们。
flags	解决PnP问题的方法：请参阅calib3d_solvePnP_flags
rvec	用于初始化迭代PnP优化算法的旋转向量，当标志为SOLVEPNP_ITERATIVE且useExtrinsicGuess设置为true时使用。
tvec	用于初始化迭代PnP优化算法的平移向量，当标志为SOLVEPNP_ITERATIVE且useExtrinsicGuess设置为true时使用。
reprojectionError	重投影误差的可选向量，即输入图像点与用估计姿态投影的3D物体点之间的RMS误差（ \( \text{RMSE} = \sqrt{\frac{\sum_{i}^{N} \left ( \hat{y_i} - y_i \right )^2}{N}} \))。

更多信息请参见Perspective-n-Point (PnP) 姿态计算

注意

• 如何在平面增强现实中使用solvePnP的示例可以在opencv_source_code/samples/python/plane_ar.py中找到
• 如果你正在使用Python
  • Numpy数组切片不能作为输入，因为solvePnP需要连续数组（由 modules/calib3d/src/solvepnp.cpp 版本2.4.9 第55行左右使用cv::Mat::checkVector() 的断言强制执行）。
  • P3P 算法要求图像点位于形状为 (N,1,2) 的数组中，因为它调用了undistortPoints（modules/calib3d/src/solvepnp.cpp 版本 2.4.9 大约第 75 行），而该函数需要 2 通道信息。
  • 因此，给定一些数据 D = np.array(...)，其中 D.shape = (N,M)，为了将其子集用作例如 imagePoints，必须有效地将其复制到一个新数组中：imagePoints = np.ascontiguousarray(D[:,:2]).reshape((N,1,2))
• 方法SOLVEPNP_DLS和SOLVEPNP_UPNP不能使用，因为当前的实现不稳定，有时会给出完全错误的结果。如果您传递了这两个标志中的任何一个，则将改为使用SOLVEPNP_EPNP方法。
• 在一般情况下，最小点数为4。对于SOLVEPNP_P3P和SOLVEPNP_AP3P方法，需要精确使用4个点（前3个点用于估计P3P问题的所有解决方案，最后一个点用于保留最小化重投影误差的最佳解决方案）。
• 使用SOLVEPNP_ITERATIVE方法和useExtrinsicGuess=true时，最小点数为3（3个点足以计算姿态，但最多有4个解）。初始解应接近全局解才能收敛。
• 使用SOLVEPNP_IPPE时，输入点必须 >= 4 且物体点必须共面。
• 使用SOLVEPNP_IPPE_SQUARE时，这是适用于标记姿态估计的特殊情况。输入点数量必须为4。物体点必须按以下顺序定义
  • 点 0: [-squareLength / 2, squareLength / 2, 0]
  • 点 1: [ squareLength / 2, squareLength / 2, 0]
  • 点 2: [ squareLength / 2, -squareLength / 2, 0]
  • 点 3: [-squareLength / 2, -squareLength / 2, 0]
• 使用SOLVEPNP_SQPNP时，输入点必须 >= 3

solvePnPRansac() [1/2]

bool cv::solvePnPRansac	(	InputArray	objectPoints,
		InputArray	imagePoints,
		InputArray	cameraMatrix,
		InputArray	distCoeffs,
		OutputArray	rvec,
		OutputArray	tvec,
		bool	useExtrinsicGuess = false,
		int	iterationsCount = 100,
		float	reprojectionError = 8.0,
		double	confidence = 0.99,
		OutputArray	inliers = noArray(),
		int	flags = SOLVEPNP_ITERATIVE )

Python
	cv.solvePnPRansac(	objectPoints, imagePoints, cameraMatrix, distCoeffs[, rvec[, tvec[, useExtrinsicGuess[, iterationsCount[, reprojectionError[, confidence[, inliers[, flags]]]]]]]]	) ->	retval, rvec, tvec, inliers
	cv.solvePnPRansac(	objectPoints, imagePoints, cameraMatrix, distCoeffs[, rvec[, tvec[, inliers[, params]]]]	) ->	retval, cameraMatrix, rvec, tvec, inliers

#include <opencv2/calib3d.hpp>

使用RANSAC方案处理错误匹配，从3D-2D点对应关系中查找物体姿态 \( {}^{c}\mathbf{T}_o \) 。

透视投影，从物体坐标系到相机坐标系

另请参见

Perspective-n-Point (PnP) 姿态计算

参数

objectPoints	物体坐标空间中的物体点数组，Nx3 1通道或1xN/Nx1 3通道，其中N为点数。此处也可传递 vector<Point3d>。
imagePoints	对应图像点的数组，Nx2 1通道或1xN/Nx1 2通道，其中N为点数。此处也可传递 vector<Point2d>。
cameraMatrix	输入相机内参矩阵 \(\cameramatrix{A}\) 。
distCoeffs	输入畸变系数向量 \(\distcoeffs\)。如果向量为 NULL/空，则假定畸变系数为零。
rvec	输出旋转向量（参见Rodrigues），与tvec一起将点从模型坐标系转换到相机坐标系。
tvec	输出平移向量。
useExtrinsicGuess	用于SOLVEPNP_ITERATIVE的参数。如果为true (1)，函数将使用提供的rvec和tvec值分别作为旋转和平移向量的初始近似值，并进一步优化它们。
iterationsCount	迭代次数。
reprojectionError	RANSAC程序使用的内点阈值。参数值为观测点和计算点投影之间的最大允许距离，以将其视为内点。
confidence	算法产生有用结果的概率。
inliers	包含objectPoints和imagePoints中内点索引的输出向量。
flags	解决PnP问题的方法（参见solvePnP）。

该函数根据一组对象点、它们对应的图像投影以及相机内参矩阵和畸变系数来估计对象姿态。该函数找到一个姿态，使重投影误差最小化，即观测投影imagePoints与投影（使用projectPoints）objectPoints之间的平方距离之和。RANSAC的使用使该函数对异常值具有鲁棒性。

注意

• 如何在实时纹理对象姿态估计中使用solvePnPRansac的示例可以在实时纹理对象姿态估计中找到。
• 用于估计最小样本集步骤的相机姿态的默认方法是SOLVEPNP_EPNP。例外情况是
  • 如果选择SOLVEPNP_P3P或SOLVEPNP_AP3P，则将使用这些方法。
  • 如果输入点数量等于4，则使用SOLVEPNP_P3P。
• 除非 flags 参数等于SOLVEPNP_P3P或SOLVEPNP_AP3P，否则使用 flags 参数定义了使用所有内点估计相机姿态的方法。在这种情况下，将改为使用SOLVEPNP_EPNP方法。

solvePnPRansac() [2/2]

bool cv::solvePnPRansac	(	InputArray	objectPoints,
		InputArray	imagePoints,
		InputOutputArray	cameraMatrix,
		InputArray	distCoeffs,
		OutputArray	rvec,
		OutputArray	tvec,
		OutputArray	inliers,
		const UsacParams &	params = UsacParams() )

Python
	cv.solvePnPRansac(	objectPoints, imagePoints, cameraMatrix, distCoeffs[, rvec[, tvec[, useExtrinsicGuess[, iterationsCount[, reprojectionError[, confidence[, inliers[, flags]]]]]]]]	) ->	retval, rvec, tvec, inliers
	cv.solvePnPRansac(	objectPoints, imagePoints, cameraMatrix, distCoeffs[, rvec[, tvec[, inliers[, params]]]]	) ->	retval, cameraMatrix, rvec, tvec, inliers

#include <opencv2/calib3d.hpp>

solvePnPRefineLM()

void cv::solvePnPRefineLM	(	InputArray	objectPoints,
		InputArray	imagePoints,
		InputArray	cameraMatrix,
		InputArray	distCoeffs,
		InputOutputArray	rvec,
		InputOutputArray	tvec,
		TermCriteria	criteria = TermCriteria(TermCriteria::EPS+TermCriteria::COUNT, 20, FLT_EPSILON) )

Python
	cv.solvePnPRefineLM(	objectPoints, imagePoints, cameraMatrix, distCoeffs, rvec, tvec[, criteria]	) ->	rvec, tvec

#include <opencv2/calib3d.hpp>

从3D-2D点对应关系和初始解中，优化姿态（将3D点从物体坐标系转换到摄像机坐标系的平移和旋转）。

另请参见

Perspective-n-Point (PnP) 姿态计算

参数

objectPoints	物体坐标空间中的物体点数组，Nx3 1通道或1xN/Nx1 3通道，其中N为点数。此处也可传递 vector<Point3d>。
imagePoints	对应图像点的数组，Nx2 1通道或1xN/Nx1 2通道，其中N为点数。此处也可传递 vector<Point2d>。
cameraMatrix	输入相机内参矩阵 \(\cameramatrix{A}\) 。
distCoeffs	输入畸变系数向量 \(\distcoeffs\)。如果向量为 NULL/空，则假定畸变系数为零。
rvec	输入/输出旋转向量（参见Rodrigues），与tvec一起将点从模型坐标系转换到相机坐标系。输入值用作初始解。
tvec	输入/输出平移向量。输入值用作初始解。
criteria	Levenberg-Marquard迭代算法的停止条件。

该函数细化了给定至少3个物体点、它们对应的图像投影、旋转和平移向量的初始解以及相机内参矩阵和畸变系数的物体姿态。该函数根据Levenberg-Marquardt迭代最小化[181] [79]过程，最小化相对于旋转和平移向量的投影误差。

solvePnPRefineVVS()

void cv::solvePnPRefineVVS	(	InputArray	objectPoints,
		InputArray	imagePoints,
		InputArray	cameraMatrix,
		InputArray	distCoeffs,
		InputOutputArray	rvec,
		InputOutputArray	tvec,
		TermCriteria	criteria = TermCriteria(TermCriteria::EPS+TermCriteria::COUNT, 20, FLT_EPSILON),
		double	VVSlambda = 1 )

Python
	cv.solvePnPRefineVVS(	objectPoints, imagePoints, cameraMatrix, distCoeffs, rvec, tvec[, criteria[, VVSlambda]]	) ->	rvec, tvec

#include <opencv2/calib3d.hpp>

从3D-2D点对应关系和初始解中，优化姿态（将3D点从物体坐标系转换到摄像机坐标系的平移和旋转）。

另请参见

Perspective-n-Point (PnP) 姿态计算

参数

objectPoints	物体坐标空间中的物体点数组，Nx3 1通道或1xN/Nx1 3通道，其中N为点数。此处也可传递 vector<Point3d>。
imagePoints	对应图像点的数组，Nx2 1通道或1xN/Nx1 2通道，其中N为点数。此处也可传递 vector<Point2d>。
cameraMatrix	输入相机内参矩阵 \(\cameramatrix{A}\) 。
distCoeffs	输入畸变系数向量 \(\distcoeffs\)。如果向量为 NULL/空，则假定畸变系数为零。
rvec	输入/输出旋转向量（参见Rodrigues），与tvec一起将点从模型坐标系转换到相机坐标系。输入值用作初始解。
tvec	输入/输出平移向量。输入值用作初始解。
criteria	Levenberg-Marquard迭代算法的停止条件。
VVSlambda	虚拟视觉伺服控制律的增益，相当于阻尼高斯-牛顿公式中的 \(\alpha\) 增益。

该函数细化了给定至少3个物体点、它们对应的图像投影、旋转和平移向量的初始解以及相机内参矩阵和畸变系数的物体姿态。该函数使用虚拟视觉伺服（VVS）[53] [185]方案，最小化相对于旋转和平移向量的投影误差。

stereoCalibrate() [1/3]

double cv::stereoCalibrate	(	InputArrayOfArrays	objectPoints,
		InputArrayOfArrays	imagePoints1,
		InputArrayOfArrays	imagePoints2,
		InputOutputArray	第一个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。,
		InputOutputArray	第一个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。,
		InputOutputArray	第二个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。,
		InputOutputArray	第二个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。,
		Size	imageSize,
		InputOutputArray	R,
		InputOutputArray	T,
		OutputArray	输入的本质矩阵。,
		OutputArray	基本矩阵，可以使用findFundamentalMat或stereoRectify进行估计。,
		OutputArray	perViewErrors,
		int	flags = CALIB_FIX_INTRINSIC,
		TermCriteria	criteria = TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 30, 1e-6) )

Python
	cv.stereoCalibrate(	objectPoints, imagePoints1, imagePoints2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, imageSize[, R[, T[, E[, F[, flags[, criteria]]]]]]	) ->	retval, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, R, T, E, F
	cv.stereoCalibrate(	objectPoints, imagePoints1, imagePoints2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, imageSize, R, T[, E[, F[, perViewErrors[, flags[, criteria]]]]]	) ->	retval, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, R, T, E, F, perViewErrors
	cv.stereoCalibrateExtended(	objectPoints, imagePoints1, imagePoints2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, imageSize, R, T[, E[, F[, rvecs[, tvecs[, perViewErrors[, flags[, criteria]]]]]]]	) ->	retval, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, R, T, E, F, rvecs, tvecs, perViewErrors

#include <opencv2/calib3d.hpp>

这是一个重载的成员函数，为方便起见而提供。它与上述函数的区别仅在于它接受的参数。

stereoCalibrate() [2/3]

double cv::stereoCalibrate	(	InputArrayOfArrays	objectPoints,
		InputArrayOfArrays	imagePoints1,
		InputArrayOfArrays	imagePoints2,
		InputOutputArray	第一个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。,
		InputOutputArray	第一个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。,
		InputOutputArray	第二个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。,
		InputOutputArray	第二个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。,
		Size	imageSize,
		InputOutputArray	R,
		InputOutputArray	T,
		OutputArray	输入的本质矩阵。,
		OutputArray	基本矩阵，可以使用findFundamentalMat或stereoRectify进行估计。,
		OutputArrayOfArrays	rvecs,
		OutputArrayOfArrays	tvecs,
		OutputArray	perViewErrors,
		int	flags = CALIB_FIX_INTRINSIC,
		TermCriteria	criteria = TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 30, 1e-6) )

Python
	cv.stereoCalibrate(	objectPoints, imagePoints1, imagePoints2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, imageSize[, R[, T[, E[, F[, flags[, criteria]]]]]]	) ->	retval, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, R, T, E, F
	cv.stereoCalibrate(	objectPoints, imagePoints1, imagePoints2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, imageSize, R, T[, E[, F[, perViewErrors[, flags[, criteria]]]]]	) ->	retval, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, R, T, E, F, perViewErrors
	cv.stereoCalibrateExtended(	objectPoints, imagePoints1, imagePoints2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, imageSize, R, T[, E[, F[, rvecs[, tvecs[, perViewErrors[, flags[, criteria]]]]]]]	) ->	retval, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, R, T, E, F, rvecs, tvecs, perViewErrors

#include <opencv2/calib3d.hpp>

校准立体摄像机设置。此函数查找两个摄像机各自的内参和它们之间的外参。

参数

objectPoints	校准模式点的向量的向量。结构与calibrateCamera相同。对于每个模式视图，两个相机都需要看到相同的物体点。因此，objectPoints.size()、imagePoints1.size()和imagePoints2.size()需要相等，并且对于每个i，objectPoints[i].size()、imagePoints1[i].size()和imagePoints2[i].size()也需要相等。
imagePoints1	第一个相机观测到的校准模式点投影的向量的向量。结构与calibrateCamera相同。
imagePoints2	第二个相机观测到的校准模式点投影的向量的向量。结构与calibrateCamera相同。
第一个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。	用于第一个相机的输入/输出相机内参矩阵，与calibrateCamera中的相同。此外，对于立体情况，可以使用附加标志，请参阅下文。
第一个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。	畸变系数的输入/输出向量，与 calibrateCamera 中的相同。
第二个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。	用于第二个相机的输入/输出第二个相机内参矩阵。参见cameraMatrix1的描述。
第二个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。	用于第二个相机的输入/输出镜头畸变系数。参见distCoeffs1的描述。
imageSize	仅用于初始化相机内参矩阵的图像大小。
R	输出旋转矩阵。该矩阵与平移向量T一起，将给定在第一个相机坐标系中的点转换到第二个相机坐标系中的点。更专业地说，R和T的元组执行从第一个相机坐标系到第二个相机坐标系的基变换。由于其对偶性，此元组等效于第一个相机相对于第二个相机坐标系的位置。
T	输出平移向量，详见上述描述。
输入的本质矩阵。	输出基本矩阵。
基本矩阵，可以使用findFundamentalMat或stereoRectify进行估计。	输出基本矩阵。
rvecs	为立体对的第一个相机坐标系中估计的每个模式视图的旋转向量输出向量（Rodrigues）（例如 std::vector<cv::Mat>）。更详细地，每个第i个旋转向量及其对应的第i个平移向量（参见下一个输出参数描述）将校准模式从物体坐标空间（其中指定了物体点）带到立体对的第一个相机的相机坐标空间。更专业地说，第i个旋转向量和平移向量的元组执行从物体坐标空间到立体对的第一个相机的相机坐标空间的基变换。
tvecs	每个模式视图估计的平移向量的输出向量，参见前一个输出参数（ rvecs ）的参数描述。
perViewErrors	为每个模式视图估计的RMS重投影误差输出向量。
flags	可以为零或以下值的组合的不同标志 CALIB_FIX_INTRINSIC 固定 cameraMatrix? 和 distCoeffs?，以便只估计 R、T、E 和 F 矩阵。 CALIB_USE_INTRINSIC_GUESS 根据指定的标志优化部分或全部内参。初始值由用户提供。 CALIB_USE_EXTRINSIC_GUESS R 和 T 包含有效初始值，这些值将进一步优化。否则，R 和 T 将初始化为模式视图的中值（每个维度分别初始化）。 CALIB_FIX_PRINCIPAL_POINT 在优化期间固定主点。 CALIB_FIX_FOCAL_LENGTH 固定 \(f^{(j)}_x\) 和 \(f^{(j)}_y\) 。 CALIB_FIX_ASPECT_RATIO 优化 \(f^{(j)}_y\) 。固定比率 \(f^{(j)}_x/f^{(j)}_y\) CALIB_SAME_FOCAL_LENGTH 强制 \(f^{(0)}_x=f^{(1)}_x\) 和 \(f^{(0)}_y=f^{(1)}_y\) 。 CALIB_ZERO_TANGENT_DIST 将每个相机的切向畸变系数设置为零并固定。 CALIB_FIX_K1,..., CALIB_FIX_K6 在优化期间不更改相应的径向畸变系数。如果设置了CALIB_USE_INTRINSIC_GUESS，则使用提供的distCoeffs矩阵中的系数。否则，将其设置为0。 CALIB_RATIONAL_MODEL 启用系数 k4、k5 和 k6。为了提供向后兼容性，应明确指定此额外标志，以使校准函数使用有理模型并返回8个系数。如果未设置该标志，则函数仅计算并返回5个畸变系数。 CALIB_THIN_PRISM_MODEL 启用系数 s1、s2、s3 和 s4。为了提供向后兼容性，应明确指定此额外标志，以使校准函数使用薄棱镜模型并返回12个系数。如果未设置该标志，则函数仅计算并返回5个畸变系数。 CALIB_FIX_S1_S2_S3_S4 薄棱镜畸变系数在优化期间不发生变化。如果设置了 CALIB_USE_INTRINSIC_GUESS，则使用提供的 distCoeffs 矩阵中的系数。否则，将其设置为0。 CALIB_TILTED_MODEL 启用系数 tauX 和 tauY。为了提供向后兼容性，应明确指定此额外标志，以使校准函数使用倾斜传感器模型并返回14个系数。如果未设置该标志，则函数仅计算并返回5个畸变系数。 CALIB_FIX_TAUX_TAUY 倾斜传感器模型的系数在优化期间不发生变化。如果设置了 CALIB_USE_INTRINSIC_GUESS，则使用提供的 distCoeffs 矩阵中的系数。否则，将其设置为0。
criteria	迭代优化算法的终止条件。

该函数估计构成立体对的两个相机之间的变换。如果计算一个物体相对于第一个相机和第二个相机的姿态（分别为\(R_1\)，\(T_1\)）和（\(R_2\)，\(T_2\)），对于相对位置和方向固定的立体相机，那么这些姿态必定相互关联。这意味着，如果已知两个相机的相对位置和方向（\(R\)，\(T\)），则在给定（\(R_1\)，\(T_1\)）的情况下，可以计算（\(R_2\)，\(T_2\)）。这就是所描述函数的作用。它计算（\(R\)，\(T\)）使得

\[R_2=R R_1\]

\[T_2=R T_1 + T.\]

因此，当给定3D点在第一个相机坐标系中的坐标表示时，可以计算其在第二个相机坐标系中的坐标表示

\[\begin{bmatrix} X_2 \\ Y_2 \\ Z_2 \\ 1 \end{bmatrix} = \begin{bmatrix} R & T \\ 0 & 1 \end{bmatrix} \begin{bmatrix} X_1 \\ Y_1 \\ Z_1 \\ 1 \end{bmatrix}.\]

可选地，它计算基本矩阵E

\[E= \vecthreethree{0}{-T_2}{T_1}{T_2}{0}{-T_0}{-T_1}{T_0}{0} R\]

其中 \(T_i\) 是平移向量 \(T\) 的分量： \(T=[T_0, T_1, T_2]^T\) 。该函数还可以计算基本矩阵F

\[F = cameraMatrix2^{-T}\cdot E \cdot cameraMatrix1^{-1}\]

除了与立体相关的信息外，该函数还可以对两个相机分别进行完整的校准。然而，由于参数空间的高维度和输入数据中的噪声，该函数可能会偏离正确解。如果可以单独高精度地估计每个相机的内参（例如，使用calibrateCamera），建议这样做，然后将CALIB_FIX_INTRINSIC标志与计算出的内参一起传递给该函数。否则，如果所有参数都同时估计，则限制某些参数是有意义的，例如，传递CALIB_SAME_FOCAL_LENGTH和CALIB_ZERO_TANGENT_DIST标志，这通常是一个合理的假设。

与calibrateCamera类似，该函数最小化所有可用视图中所有点的总重投影误差。该函数返回重投影误差的最终值。

stereoCalibrate() [3/3]

double cv::stereoCalibrate	(	InputArrayOfArrays	objectPoints,
		InputArrayOfArrays	imagePoints1,
		InputArrayOfArrays	imagePoints2,
		InputOutputArray	第一个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。,
		InputOutputArray	第一个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。,
		InputOutputArray	第二个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。,
		InputOutputArray	第二个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。,
		Size	imageSize,
		OutputArray	R,
		OutputArray	T,
		OutputArray	输入的本质矩阵。,
		OutputArray	基本矩阵，可以使用findFundamentalMat或stereoRectify进行估计。,
		int	flags = CALIB_FIX_INTRINSIC,
		TermCriteria	criteria = TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 30, 1e-6) )

Python
	cv.stereoCalibrate(	objectPoints, imagePoints1, imagePoints2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, imageSize[, R[, T[, E[, F[, flags[, criteria]]]]]]	) ->	retval, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, R, T, E, F
	cv.stereoCalibrate(	objectPoints, imagePoints1, imagePoints2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, imageSize, R, T[, E[, F[, perViewErrors[, flags[, criteria]]]]]	) ->	retval, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, R, T, E, F, perViewErrors
	cv.stereoCalibrateExtended(	objectPoints, imagePoints1, imagePoints2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, imageSize, R, T[, E[, F[, rvecs[, tvecs[, perViewErrors[, flags[, criteria]]]]]]]	) ->	retval, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, R, T, E, F, rvecs, tvecs, perViewErrors

#include <opencv2/calib3d.hpp>

这是一个重载的成员函数，为方便起见而提供。它与上述函数的区别仅在于它接受的参数。

stereoRectify()

void cv::stereoRectify	(	InputArray	第一个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。,
		InputArray	第一个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。,
		InputArray	第二个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。,
		InputArray	第二个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。,
		Size	imageSize,
		InputArray	R,
		InputArray	T,
		OutputArray	一个可能的旋转矩阵。,
		OutputArray	另一个可能的旋转矩阵。,
		OutputArray	P1,
		OutputArray	P2,
		OutputArray	Q,
		int	flags = CALIB_ZERO_DISPARITY,
		double	alpha = -1,
		Size	newImageSize = Size(),
		Rect *	validPixROI1 = 0,
		Rect *	validPixROI2 = 0 )

Python
	cv.stereoRectify(	cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, imageSize, R, T[, R1[, R2[, P1[, P2[, Q[, flags[, alpha[, newImageSize]]]]]]]]	) ->	R1, R2, P1, P2, Q, validPixROI1, validPixROI2

#include <opencv2/calib3d.hpp>

计算已校准立体摄像机每个摄像头的校正变换。

参数

第一个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。	第一个相机内参矩阵。
第一个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。	第一个相机畸变参数。
第二个相机的相机矩阵\(K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\)。	第二个相机内参矩阵。
第二个相机的畸变系数输入向量\((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含4、5、8、12或14个元素。如果向量为NULL/空，则假定畸变系数为零。	第二个相机畸变参数。
imageSize	用于立体校准的图像大小。
R	从第一个相机坐标系到第二个相机的旋转矩阵，参见stereoCalibrate。
T	从第一个相机坐标系到第二个相机的平移向量，参见stereoCalibrate。
一个可能的旋转矩阵。	第一个相机的输出 3x3 校正变换（旋转矩阵）。此矩阵将给定在未校正的第一个相机坐标系中的点转换到校正后的第一个相机坐标系中的点。更专业地说，它执行从未校正的第一个相机坐标系到校正后的第一个相机坐标系的基变换。
另一个可能的旋转矩阵。	第二个相机的输出 3x3 校正变换（旋转矩阵）。此矩阵将给定在未校正的第二个相机坐标系中的点转换到校正后的第二个相机坐标系中的点。更专业地说，它执行从未校正的第二个相机坐标系到校正后的第二个相机坐标系的基变换。
P1	第一个相机在新（校正后的）坐标系中的输出3x4投影矩阵，即将校正后的第一个相机坐标系中的点投影到校正后的第一个相机图像中。
P2	第二个相机在新（校正后的）坐标系中的输出3x4投影矩阵，即将校正后的第一个相机坐标系中的点投影到校正后的第二个相机图像中。
Q	输出 \(4 \times 4\) 视差到深度映射矩阵（参见reprojectImageTo3D）。
flags	操作标志，可以为零或CALIB_ZERO_DISPARITY。如果设置了该标志，函数将使每个相机的主点在校正后的视图中具有相同的像素坐标。如果未设置该标志，函数仍可能在水平或垂直方向（取决于对极线的方向）移动图像以最大化有效图像区域。
alpha	自由缩放参数。如果为-1或不存在，函数执行默认缩放。否则，参数应在0到1之间。alpha=0表示校正后的图像被缩放和平移，以便只有有效像素可见（校正后没有黑色区域）。alpha=1表示校正后的图像被抽取和移动，以便原始图像中来自相机的所有像素都保留在校正后的图像中（没有源图像像素丢失）。任何中间值都会产生介于这两个极端情况之间的结果。
newImageSize	校正后的新图像分辨率。应将相同的大小传递给initUndistortRectifyMap（参见OpenCV示例目录中的stereo_calib.cpp示例）。当传递(0,0)（默认）时，它设置为原始imageSize。将其设置为更大的值可以帮助您保留原始图像中的细节，尤其是在径向畸变很大时。
validPixROI1	校正图像中所有像素都有效的可选输出矩形。如果alpha=0，ROI覆盖整个图像。否则，它们可能更小（参见下图）。
validPixROI2	校正图像中所有像素都有效的可选输出矩形。如果alpha=0，ROI覆盖整个图像。否则，它们可能更小（参见下图）。

该函数计算每个相机的旋转矩阵，这些矩阵（实际上）使两个相机的图像平面处于同一平面。因此，这将使所有对极线平行，从而简化了密集的立体对应问题。该函数将由stereoCalibrate计算出的矩阵作为输入。作为输出，它提供了两个旋转矩阵以及新坐标系中的两个投影矩阵。该函数区分以下两种情况

• 水平立体：第一和第二个相机视图主要沿x轴相互偏移（可能有小的垂直偏移）。在校正后的图像中，左右相机中对应的对极线是水平的，并且具有相同的y坐标。P1和P2看起来像

  \[\texttt{P1} = \begin{bmatrix} f & 0 & cx_1 & 0 \\ 0 & f & cy & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix}\]

  \[\texttt{P2} = \begin{bmatrix} f & 0 & cx_2 & T_x \cdot f \\ 0 & f & cy & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} ,\]

  \[\texttt{Q} = \begin{bmatrix} 1 & 0 & 0 & -cx_1 \\ 0 & 1 & 0 & -cy \\ 0 & 0 & 0 & f \\ 0 & 0 & -\frac{1}{T_x} & \frac{cx_1 - cx_2}{T_x} \end{bmatrix} \]

  其中 \(T_x\) 是相机之间的水平偏移，如果设置了CALIB_ZERO_DISPARITY，则 \(cx_1=cx_2\)。

• 垂直立体：第一和第二个相机视图主要在垂直方向上相互偏移（可能在水平方向上也有少量偏移）。校正图像中的对极线是垂直的，并且具有相同的x坐标。P1和P2看起来像

  \[\texttt{P1} = \begin{bmatrix} f & 0 & cx & 0 \\ 0 & f & cy_1 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix}\]

  \[\texttt{P2} = \begin{bmatrix} f & 0 & cx & 0 \\ 0 & f & cy_2 & T_y \cdot f \\ 0 & 0 & 1 & 0 \end{bmatrix},\]

  \[\texttt{Q} = \begin{bmatrix} 1 & 0 & 0 & -cx \\ 0 & 1 & 0 & -cy_1 \\ 0 & 0 & 0 & f \\ 0 & 0 & -\frac{1}{T_y} & \frac{cy_1 - cy_2}{T_y} \end{bmatrix} \]

  其中 \(T_y\) 是相机之间的垂直偏移，如果设置了CALIB_ZERO_DISPARITY，则 \(cy_1=cy_2\)。

如你所见，P1和P2的前三列将有效地成为新的“校正”相机矩阵。这些矩阵与R1和R2一起，可以传递给initUndistortRectifyMap，以初始化每个相机的校正映射。

请参阅下面的stereo_calib.cpp示例截图。一些红色水平线穿过相应的图像区域。这意味着图像校正良好，这是大多数立体对应算法所依赖的。绿色矩形是roi1和roi2。您会看到它们的内部都是有效像素。

image

stereoRectifyUncalibrated()

bool cv::stereoRectifyUncalibrated	(	InputArray	3x3基本矩阵。,
		InputArray	包含第一组点的1xN数组。,
		InputArray	基本矩阵，可以使用findFundamentalMat或stereoRectify进行估计。,
		Size	imgSize,
		OutputArray	H1,
		OutputArray	H2,
		double	threshold = 5 )

Python
	cv.stereoRectifyUncalibrated(	points1, points2, F, imgSize[, H1[, H2[, threshold]]]	) ->	retval, H1, H2

#include <opencv2/calib3d.hpp>

计算未经校准的立体摄像机的校正变换。

参数

3x3基本矩阵。	第一幅图像中的特征点数组。
包含第一组点的1xN数组。	第二幅图像中对应的点。支持与findFundamentalMat相同的格式。
基本矩阵，可以使用findFundamentalMat或stereoRectify进行估计。	输入基本矩阵。它可以使用findFundamentalMat从同一组点对计算。
imgSize	图像大小。
H1	第一张图像的输出校正单应矩阵。
H2	第二张图像的输出校正单应矩阵。
RANSAC参数。它是点到像素中对极线的最大距离，超过此距离的点将被视为异常值，不用于计算最终的基本矩阵。它可以设置为1-3左右，具体取决于点定位的精度、图像分辨率和图像噪声。	用于滤除异常值的可选阈值。如果参数大于零，所有不符合对极几何的点对（即，对于这些点， \(|\texttt{points2[i]}^T \cdot \texttt{F} \cdot \texttt{points1[i]}|>\texttt{threshold}\) ）在计算单应性之前被拒绝。否则，所有点都被视为内点。

该函数在不知道相机内参及其在空间中相对位置的情况下计算校正变换，这解释了“未校准”后缀。与stereoRectify的另一个相关区别是，该函数输出的不是物体（3D）空间中的校正变换，而是由单应矩阵H1和H2编码的平面透视变换。该函数实现了算法[120]。

注意

虽然该算法不需要知道相机的内参，但它严重依赖于对极几何。因此，如果相机镜头有显著畸变，最好在计算基本矩阵并调用此函数之前对其进行校正。例如，可以使用calibrateCamera分别估计立体相机的每个头的畸变系数。然后，可以使用[120]校正图像，或者仅使用undistortPoints校正点坐标。

triangulatePoints()

void cv::triangulatePoints	(	InputArray	projMatr1,
		InputArray	projMatr2,
		InputArray	projPoints1,
		InputArray	projPoints2,
		OutputArray	points4D )

Python
	cv.triangulatePoints(	projMatr1, projMatr2, projPoints1, projPoints2[, points4D]	) ->	points4D

#include <opencv2/calib3d.hpp>

此函数通过使用立体摄像机的观测数据重建3D点（齐次坐标）。

参数

projMatr1	第一个相机的3x4投影矩阵，即此矩阵将世界坐标系中的3D点投影到第一张图像中。
projMatr2	第二个相机的3x4投影矩阵，即此矩阵将世界坐标系中的3D点投影到第二张图像中。
projPoints1	第一张图像中的2xN特征点数组。在C++版本中，它也可以是特征点向量或1xN或Nx1大小的双通道矩阵。
projPoints2	第二张图像中对应的2xN点数组。在C++版本中，它也可以是特征点向量或1xN或Nx1大小的双通道矩阵。
points4D	重建点在齐次坐标系中的4xN数组。这些点在世界坐标系中返回。

注意

请记住，所有输入数据都应为浮点类型，此函数才能正常工作。

如果使用stereoRectify中的投影矩阵，则返回的点将表示在第一个相机的校正坐标系中。

另请参见

reprojectImageTo3D

undistort()

void cv::undistort	(	InputArray	src,
		OutputArray	dst,
		InputArray	cameraMatrix,
		InputArray	distCoeffs,
		InputArray	newCameraMatrix = noArray() )

Python
	cv.undistort(	src, cameraMatrix, distCoeffs[, dst[, newCameraMatrix]]	) ->	dst

#include <opencv2/calib3d.hpp>

变换图像以补偿镜头畸变。

该函数对图像进行变换，以补偿径向和切向镜头畸变。

该函数是initUndistortRectifyMap（R为单位矩阵）和remap（使用双线性插值）的简单组合。有关所执行变换的详细信息，请参见前一个函数。

目标图像中没有对应源像素的像素将填充零（黑色）。

校正图像中可见的源图像的特定子集可以通过 newCameraMatrix 进行调节。您可以使用getOptimalNewCameraMatrix根据您的要求计算合适的 newCameraMatrix。

相机矩阵和畸变参数可以使用calibrateCamera确定。如果图像分辨率与校准阶段使用的分辨率不同，则 \(f_x, f_y, c_x\) 和 \(c_y\) 需要相应地缩放，而畸变系数保持不变。

参数

src	输入（畸变）图像。
dst	输出（校正）图像，其大小和类型与src相同。
cameraMatrix	输入相机矩阵 \(A = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\) 。
distCoeffs	输入畸变系数向量 \((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含 4、5、8、12 或 14 个元素。如果向量为 NULL/空，则假定畸变系数为零。
newCameraMatrix	畸变图像的相机矩阵。默认情况下，它与 cameraMatrix 相同，但您可以通过使用不同的矩阵来额外缩放和移动结果。

undistortImagePoints()

void cv::undistortImagePoints	(	InputArray	src,
		OutputArray	dst,
		InputArray	cameraMatrix,
		InputArray	distCoeffs,
		TermCriteria	= TermCriteria(TermCriteria::MAX_ITER+TermCriteria::EPS, 5, 0.01) )

Python
	cv.undistortImagePoints(	src, cameraMatrix, distCoeffs[, dst[, arg1]]	) ->	dst

#include <opencv2/calib3d.hpp>

计算畸变校正后的图像点位置。

参数

src	观测点位置，2xN/Nx2 1通道或1xN/Nx1 2通道（CV_32FC2或CV_64FC2）（或vector<Point2f>）。
dst	输出校正后的点位置（1xN/Nx1 2通道或vector<Point2f>）。
cameraMatrix	相机矩阵 \(\vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\) 。
distCoeffs	畸变系数

undistortPoints() [1/2]

void cv::undistortPoints	(	InputArray	src,
		OutputArray	dst,
		InputArray	cameraMatrix,
		InputArray	distCoeffs,
		InputArray	R,
		InputArray	P,
		TermCriteria	criteria )

Python
	cv.undistortPoints(	src, cameraMatrix, distCoeffs[, dst[, R[, P]]]	) ->	dst
	cv.undistortPointsIter(	src, cameraMatrix, distCoeffs, R, P, criteria[, dst]	) ->	dst

#include <opencv2/calib3d.hpp>

这是一个重载的成员函数，为方便起见而提供。它与上述函数的区别仅在于它接受的参数。

注意

undistortPoints的默认版本执行5次迭代以计算校正后的点。

undistortPoints() [2/2]

void cv::undistortPoints	(	InputArray	src,
		OutputArray	dst,
		InputArray	cameraMatrix,
		InputArray	distCoeffs,
		InputArray	R = noArray(),
		InputArray	P = noArray() )

Python
	cv.undistortPoints(	src, cameraMatrix, distCoeffs[, dst[, R[, P]]]	) ->	dst
	cv.undistortPointsIter(	src, cameraMatrix, distCoeffs, R, P, criteria[, dst]	) ->	dst

#include <opencv2/calib3d.hpp>

从观测点坐标计算理想点坐标。

该函数类似于undistort和initUndistortRectifyMap，但它作用于稀疏点集而非栅格图像。此外，该函数执行projectPoints的逆变换。对于3D物体，它不重建其3D坐标，但对于平面物体，如果指定了正确的R，它会重建，直到一个平移向量。

对于每个观测点坐标 \((u, v)\)，函数计算

\[ \begin{array}{l} x^{"} \leftarrow (u - c_x)/f_x \\ y^{"} \leftarrow (v - c_y)/f_y \\ (x',y') = undistort(x^{"},y^{"}, \texttt{distCoeffs}) \\ {[X\,Y\,W]} ^T \leftarrow R*[x' \, y' \, 1]^T \\ x \leftarrow X/W \\ y \leftarrow Y/W \\ \text{only performed if P is specified:} \\ u' \leftarrow x {f'}_x + {c'}_x \\ v' \leftarrow y {f'}_y + {c'}_y \end{array} \]

其中 undistort 是一种近似迭代算法，它从归一化的畸变点坐标中估计归一化的原始点坐标（“归一化”意味着坐标不依赖于相机矩阵）。

该函数既可用于立体相机头也可用于单目相机（当R为空时）。

参数

src	观测点坐标，2xN/Nx2 1通道或1xN/Nx1 2通道（CV_32FC2或CV_64FC2）（或vector<Point2f>）。
dst	输出校正和反向透视变换后的理想点坐标（1xN/Nx1 2通道或vector<Point2f>）。如果矩阵P是单位矩阵或省略，dst将包含归一化点坐标。
cameraMatrix	相机矩阵 \(\vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\) 。
distCoeffs	输入畸变系数向量 \((k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6[, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\)，包含 4、5、8、12 或 14 个元素。如果向量为 NULL/空，则假定畸变系数为零。
R	物体空间中的校正变换（3x3矩阵）。stereoRectify计算的R1或R2可在此处传递。如果矩阵为空，则使用单位变换。
P	新相机矩阵（3x3）或新投影矩阵（3x4） \(\begin{bmatrix} {f'}_x & 0 & {c'}_x & t_x \\ 0 & {f'}_y & {c'}_y & t_y \\ 0 & 0 & 1 & t_z \end{bmatrix}\)。stereoRectify计算的P1或P2可在此处传递。如果矩阵为空，则使用单位新相机矩阵。

validateDisparity()

void cv::validateDisparity	(	InputOutputArray	disparity,
		InputArray	cost,
		int	minDisparity,
		int	numberOfDisparities,
		int	disp12MaxDisp = 1 )

Python
	cv.validateDisparity(	disparity, cost, minDisparity, numberOfDisparities[, disp12MaxDisp]	) ->	disparity

#include <opencv2/calib3d.hpp>

使用左右检查验证视差。“cost”矩阵应由立体对应算法计算得出。